Проекционно-сеточный метод.

Основная идея метода заключается в том, что на участках оси независимой переменной τ в качестве решения y принимается функция определенного типа, но с неизвестными пока параметрами (коэффициентами). Выражения для функции и ее производных подставляются в решаемое уравнение. Записывается выражение для функционала S, который представляет собой сумму квадратов невязок (разностей значений правой и левой частей уравнения) для ряда значений независимой переменной. Коэффициенты аппроксимирующей функции находятся путем минимизации функционала S. Можно использовать либо методы безусловной оптимизации, либо прямые методы (что будет рассмотрено далее).

В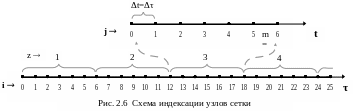 области определения функции y выделяются узловые точки i с шагом . Назначается последовательность интервалов интегрирования z, каждый из которых включает несколько узловых точек j. В пределах каждого интервала интегрирования используется локальная независимая переменная t.

Решение обыкновенного дифференциального уравнения 1го порядка:

(2.23)

где А, В – заданные коэффициенты уравнения, F – воздействие.

В качестве функции аппроксимирующей решение y на каждом интервале интегрирования чаще всего принимается полином kn^ой степени:

(2.24)

Соответственно выражения для производной:

(2.25)

где a₁a_kn – коэффициенты полинома, подлежащие определению. Значения коэффициента а₀ определяется из удовлетворения начальному условию или решению полученному на предыдущем интервале интегрирования:

(2.26)

Подставляя выражения для y, y в решаемое уравнение получим:

(2.27)

Сумма квадратов невязок (разностей значений правой и левой частей уравнения) по всем точкам рассматриваемого интервала интегрирования (j=0m) имеет вид:

(2.28)

Значение функционала S будет минимальным при выполнении условий:

(2.29)

Удовлетворяя каждому приведенному условию можно записать СЛАУ имеющую коэффициенты матрицы (МА) и элементы вектора правой части (МВ) определяемые зависимостями:

(2.30)

где L – индекс строки матрицы (line), C – индекс столбца (column).

В общем случае 1  L  kn, 1  C  kn.

Для дифференциального уравнения первого порядка решение которого аппроксимируется полиномом, порядок матрицы численно равен порядку аппроксимирующего полинома.

Решив полученную СЛАУ найдем значения коэффициентов полинома a₁a_kn.

Следует отметить, что при постоянных значениях коэффициентов уравнения A, B и при фиксируемых значениях Δτ и m коэффициенты матрицы MA_L,C одинаковы для всех интервалов интегрирования, а изменяются только значения MB_L.

Рассмотрим конкретный пример аппроксимации решения полиномом третьего порядка.

(2.31)