- •4.1 Назначение и виды арматуры для железобетонных конструкций
- •4.2 Механические свойства арматурных сталей
- •4.3 Сварные арматурные изделия, стыки арматуры
- •Вопросы для самоконтроля по теме 4
- •Тема 7,8 Экспериментально-статистическая оценка модуля упругости и упруго-пластических характеристик бетона при кратковременном центральном сжатии методом линейного корреляционного анализа.
- •К вычислению коэффициента корреляции
Тема 7,8 Экспериментально-статистическая оценка модуля упругости и упруго-пластических характеристик бетона при кратковременном центральном сжатии методом линейного корреляционного анализа.
В результате испытаний бетонной призмы на центральное сжатие с постоянной скоростью приложения нагрузки (через 2,0 МПа в минуту) мы получили следующую опытную зависимость между напряжениями σ и деформации ε, фиксируемыми в процессе испытаний, представленную в таблице 7.1 и на рис. 7.1.
Необходимо
выявить: существует ли линейная
корреляционная связь между
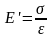
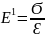 и σ.
При наличии этой связи - оценить ее
количественно линейным корреляционным
уравнением с допускаемой при этом
погрешностью, а также выявить
упругопластические характеристики
бетона (модуль упругости, коэффициент
пластичности и др.) и аналитическое
выражение зависимости (σ - ε), (σ -Е).
и σ.
При наличии этой связи - оценить ее
количественно линейным корреляционным
уравнением с допускаемой при этом
погрешностью, а также выявить
упругопластические характеристики
бетона (модуль упругости, коэффициент
пластичности и др.) и аналитическое
выражение зависимости (σ - ε), (σ -Е).
Различают функциональную и корреляционную зависимости между двумя свойствами, признаками или характеристиками материалов, функциональная зависимость - это такая зависимость, когда каждой отдельной величине соответствует строго определенная другая величина, например, каждому радиусу круга соответствует строго определенная площадь круга. Корреляционная зависимость - это такая зависимость между двумя свойствами или характеристиками, когда одной независимой величине (например, напряжению) соответствует несколько переменных, варьирующих около средней величины (например, деформация ε или секущий модуль деформаций Е’ по показаниям четырех тензометров по боковым граням призмы). Причем, числу наблюдений над одним свойством (напряжением), должно соответствовать такое же число наблюдений над другим (деформацией), т.е. должны быть связаны пары результатов наблюдений. Корреляционная связь может быть прямолинейной и криволинейной (1). Наиболее простым способом первичного определения связи между двумя свойствами является способ графического изображения результатов вычислений. Откладывая по оси абсцисс данные одного свойства (напряжения), а по оси ординат соответствующие ими значения другого свойства (относительные деформации ε и Е’, получают группу точек (см. рис. 7.1 и рис. 7.2 ). Так как на исследуемые зависимости (σ - ε), (Е’- σ) оказывают влияние целый ряд порой неизвестных и не подлежащих учету факторов (неоднородность бетона по сечению, неточность снятия отсчетов по силоизмерителю и деформометрам), то точки на графиках (σ - ε) и (Е’- σ) будут более-менее разбросаны (особенно если учесть показания каждого из четырех тензодатчиков). Однако, если между изучаемыми свойствами или параметрами есть связь, то в расположении опытных точек намечается некоторая правильность. На рис. 2 видна прямолинейная зависимость (Е’- σ).
Корреляционная связь между двумя варьирующими свойствами сама по себе не определяет причины зависимости между ними. Корреляция устанавливает только величину связи между двумя свойствами, причинную же связь между ними нужно искать в самой сущности явления. Например, искривление диаграммы сжатия бетона (σ - ε) объясняется быстронатекающими деформациями ползучести цементного камня, причем - нелинейными деформациями.
Величиной, выражающей прямолинейную зависимость между двумя свойствами, является коэффициент корреляции, обозначаемый буквой "r" и колеблющейся в пределах -1≤r≤+1. Знак(«+»)указывает на положительную связь, а знак («-») на отрицательную. При «r»=1 имеем функциональную зависимость между исследуемыми свойствами. При «r»=0 связь или отсутствует или имеет криволинейный характер. Таким образом, чем ближе коэффициент корреляции к единице, тем больше связь между изучаемыми свойствами.
Коэффициент корреляции r вычисляют по формуле (7.1):
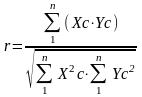 (7.1)
(7.1)
где
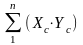 -
сумма произведений отклонений отдельных
вариант Vx1
, Vy
того (x) и другого (y)
свойств от соответствующих им средних
арифметических Mx
и My;
-
сумма произведений отклонений отдельных
вариант Vx1
, Vy
того (x) и другого (y)
свойств от соответствующих им средних
арифметических Mx
и My;
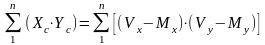 (7.2)
(7.2)
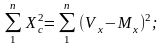
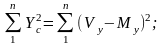 (7.3)
(7.3)
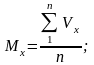
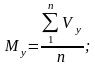 (7.4)
(7.4)
n -число наблюдений (вариант каждого ряда).
Средняя ошибка коэффициента корреляции mr:
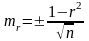 (7.5)
(7.5)
Достоверность коэффициента корреляции (линейного корреляционного уравнения или связи) оценивается отношением коэффициента корреляции r к его средней ошибке mr. Если это отношение равно 4 или больше, то коэффициент корреляции считается достоверным и наличие связи между двумя свойствами является доказанной, в противном случае - нельзя сделать заключения о достоверности связи между изучаемыми свойствами. Итак, линейная корреляционная зависимость достоверна если:
 (7.6)
(7.6)
r и r/mr доказывают на количественную оценку связи между двумя величинами, но не выражают эту связь в виде уравнения.
При экспериментально-статистических исследованиях по выявлению зависимости между двумя величинами X и Y одной из величин (например, напряжению X = σ) дают различные значения, а значения другой величины (например, секущего модуля деформаций бетона Y = Е’) определяют опытным путем. В этом случае величина X = σ является уже не статистической, а независимой переменной заданной без ошибки. Величина Y = Е’, являющаяся зависимой переменной, определяется в результате опыта и поэтому она неизбежно будет иметь разные значения (например, в разных образцах - близнецах). При установлении уравнения связи в этом случае для величины Y = Е’ нужно взять ее средние значения (например в одной призме по показаниям 4-х измерителей деформаций), соответствующие заданным значениям величины X = σ.
Линейное корреляционное уравнение выражается следующей формулой:
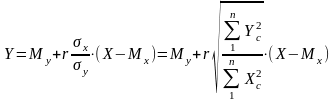 (7.7)
(7.7)
σ x, σ y - средние квадратические отклонения:
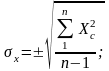
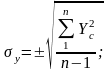 (7.8)
(7.8)
Среднее арифметическое Mx; My дает представление о средней величине изучаемого свойства, а среднеквадратическое отклонение σ x, σ y характеризует среднюю изменчивость изучаемого свойства и имеет ту же размерность, что и Mx и My.
Средняя ошибка линейного корреляционного уравнения (7.7), определяющая возможную погрешность его, вычисляется по формуле:
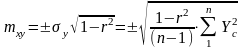 (7.9)
(7.9)
Статистические величины σ y, mxy служат для оценки надежности полученного линейного корреляционного уравнения (7.7). Теория вероятностей доказывает, что при повторной опытной проверке уравнения (7.7) по правилу "трех сигм" или "трех ошибок" в 683 случаях из 1000 получают величины My и “Y” отклоняющиеся в ту или другую сторону от вычисленных величин по уравнениям (7.4), (7.7) соответственно не более чем на одну σ y или mxy. В 954 случаях из 1000 результаты не входят за пределы ±2σ y или ±2 mxy и в 997 случаях из 1000 за пределы ±3σ y или ±3 mxy.
Если необходимо определить “Х” по “Y”, то ни в коем случае нельзя это делать алгебраически из линейного корреляционного уравнения (7.7). В этом случае надо составить новое уравнение, приняв “Y” за независимую переменную величину, а “Х” за зависимую переменную, т.е.:
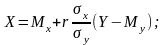
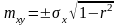
Теперь перейдем непосредственно к установлению и вычислению линейного корреляционного уравнения (7.7) для Е’ и σ по опытным их значениям, представленным в таблице 7.1.
Для вычисления коэффициента корреляции составляем таблицу 7.2. В этой таблице за варианты Vx принято σ, а за варианты Vy – Е’ (опытные значения). В таблице 7.2 показаны также последовательность вычислений и их результаты.
По
полученным в таблице 2 результатам
находим величину
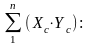
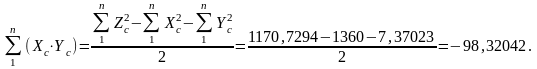
Согласно
(7.1)
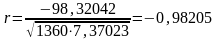 (близок к 1).
(близок к 1).
По
(7.5)
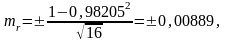
по
(7.6)
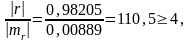 т.е. наличие линейной корреляционной
зависимости (7.7) между Y=Е’
и Х= σ доказано с большой достоверностью.
т.е. наличие линейной корреляционной
зависимости (7.7) между Y=Е’
и Х= σ доказано с большой достоверностью.
Согласно (7.7) линейное корреляционное уравнение связи (Е’- σ) будет следующим:
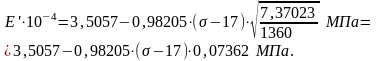
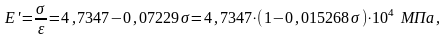 (7.11)
(7.11)
где σ в МПа.
Граничные значения E’ из уравнения (7.11): при σ=0 E’=Eo=4,7347·104 МПа; при σ=Rb; E’=E’Rb=2,4214·104 МПа.
Секущий модуль деформаций бетона в зависимости от его граничных значений:
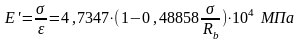 (7.12)
(7.12)
Средняя ошибка линейного корреляционного уравнения (7.11) согласно (7.9):
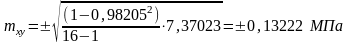
Статистическая обработка опубликованных результатов испытаний многочисленных авторов стран СНГ, а также результаты исследований дальнего зарубежья позволила профессору Макаренко Л.П. (7.2) установить что зависимость «напряжение – секущий модуль деформаций» (σ – E’) при сжатии призменных образцов, загружаемых с постоянной скоростью загружения Vσ, является линейной вплоть до разрушения бетонного образца при линейной зависимости (σ- ε).
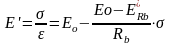 (7.13)
(7.13)
Упруго-пластические характеристики бетона при текущем напряжении кратковременного центрального сжатия С≤ σ ≤ Rb (коэффициент упругости ν, пластичности λ, характеристика φ и удельная деформация С быстронатекающей (кратковременной) ползучести, удельные упругие δуп и полные δ силовые деформации) выраженные через секущий модуль деформации Е’ по (7.13) и их взаимосвязь:
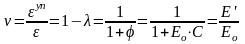 (7.14)
(7.14)
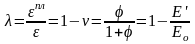 (7.15)
(7.15)
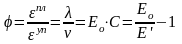 (7.16)
(7.16)
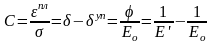 (7.17)
(7.17)
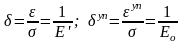 (7.18)
(7.18)
Быстронатекающая (кратковременная) деформация ползучести бетона:
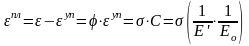 (7.19)
(7.19)
В таблице 7.1, таблице 7.3 и на рис. 7.1, 7.2 и 7.3 показано в численном виде и графически сопоставление теоретических (корреляционных) зависимостей (σ - ε), (E’ - σ), (E - σ), (ν - σ), (λ - σ), (С - σ), (φ - σ), (δ - σ), (εпл - σ) по вышеприведенным формулам при значении E’ из линейного корреляционного уравнения (7.11) с опытными значениями вышеуказанных величин, полученным по тем же формулам, но при опытных значениях E’.
Как
видно из рис. 7.2 и рис. 7.3 , коэффициенты
упругости ν и пластичности λ, также как
и Е’, находятся в линейной зависимости
от уровня напряжений
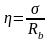 ,
а остальные параметры бетона – в
нелинейной зависимости.
,
а остальные параметры бетона – в
нелинейной зависимости.
Фактическое значение модуля упругости бетона Ео=4,7347·104 МПа. По СНБ 5.03.01-02 начальный модуль упругости бетона Ео=Ео4=4,7347(1-0,48858·0,4)·104=3,809·104 МПа, т.е. на 19,6% меньше Ео.
Таким образом, при помощи линейного корреляционного анализа зависимости (E’ - σ) представилась возможность оценить в аналитической форме зависимость (σ - ε) и другие упруго-пластические характеристики бетона при центральном сжатии.
Как видно из таблицы 1 и таблицы 3, максимальное отклонение теоретических значений искомых величин от опытных соответствует минимальному уровню напряжений η=0,062, что обусловлено большой погрешностью при оценке деформаций при малых уровнях напряжений. Зафиксировать деформации сжатия бетона в момент его разрушения очень трудно и не всегда удается. В силу вышеизложенного при установлении линейной корреляционной зависимости (E’ - σ) отсчеты по первой и последней (в момент разрушения) ступенях рекомендуется не учитывать.
Вычисление коэффициента корреляции r и установление линейной корреляционной зависимости (E’ - σ) с оценкой её погрешности mxy может быть произведено также при помощи ПЭВМ по специально разработанной программе.
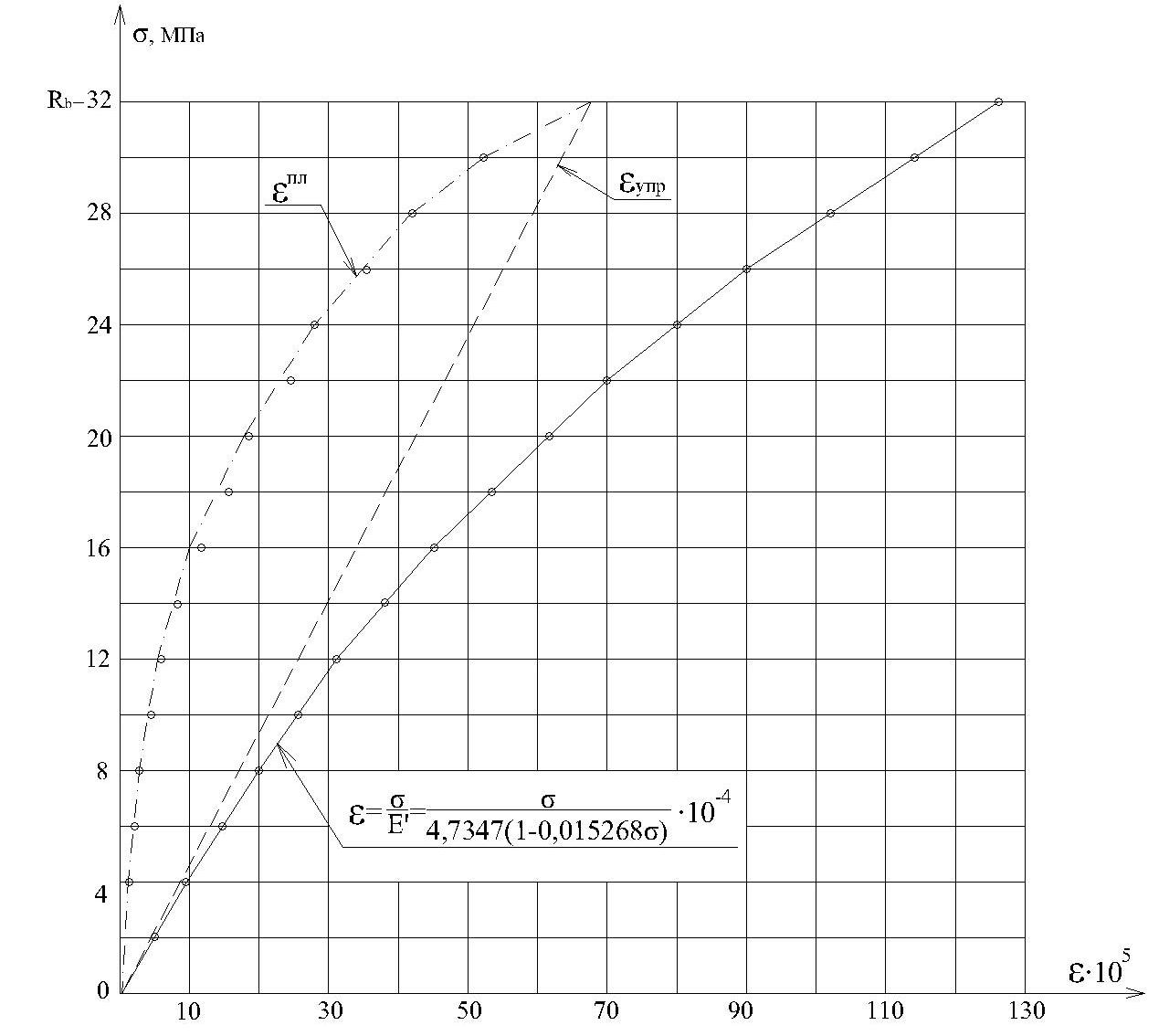
Р![]() исунок
7.1- Опытные и теоретические зависимости
(σ-ε); (σ-εпл);
(σ-εупр)
согласно данным таблицы 1: о – опытные
точки, усредненные по показаниям
тензодатчиков; -теоретические
(опытно-корреляционные) кривые, исходя
из линейной корреляционной зависимости
(E’-σ).
исунок
7.1- Опытные и теоретические зависимости
(σ-ε); (σ-εпл);
(σ-εупр)
согласно данным таблицы 1: о – опытные
точки, усредненные по показаниям
тензодатчиков; -теоретические
(опытно-корреляционные) кривые, исходя
из линейной корреляционной зависимости
(E’-σ).
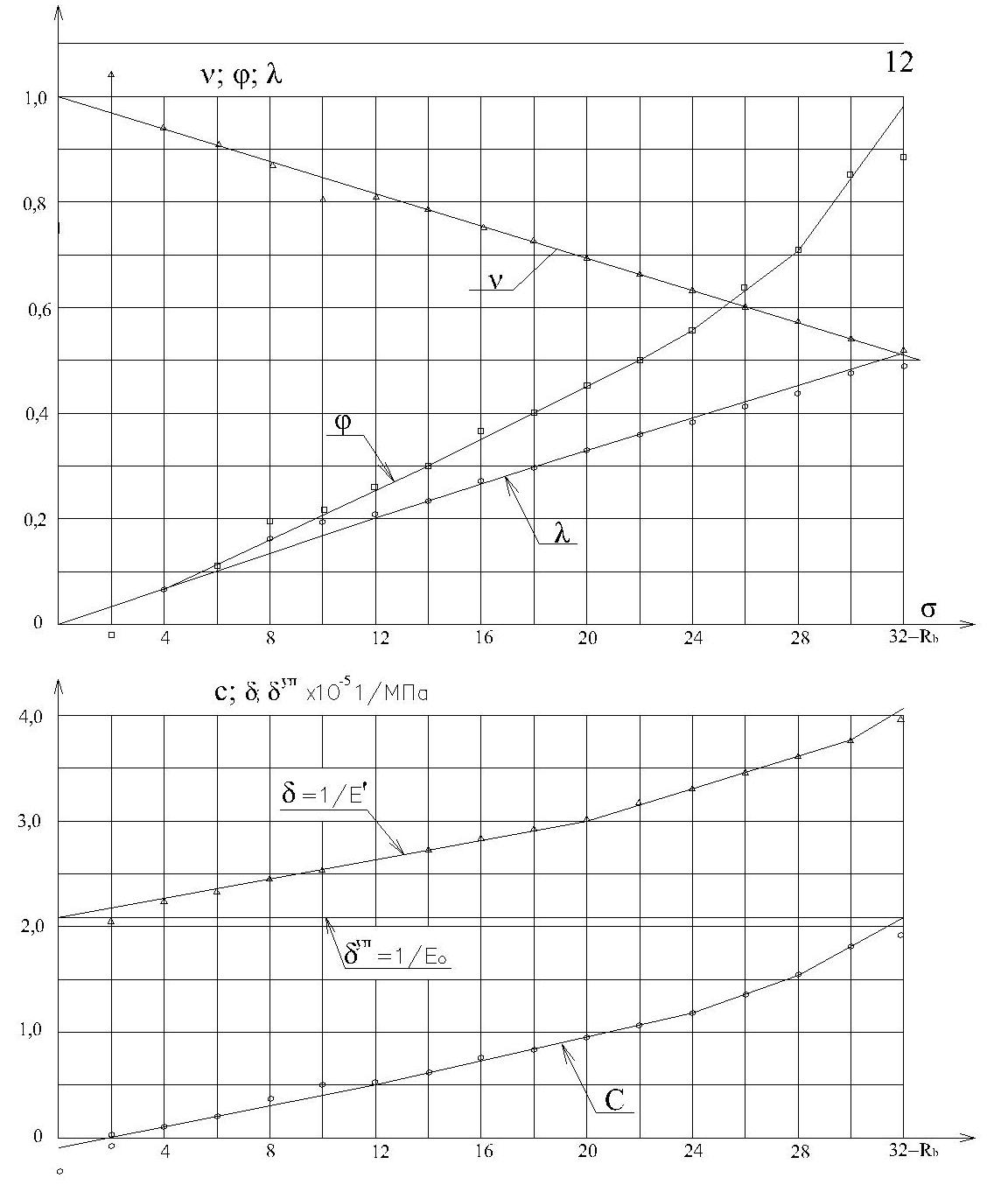
Рисунок 7.3- Опытные и теоретические (корреляционные) зависимости (ν-σ); (φ-σ); (λ-σ), (С-σ), (δ -σ) при опытных и линейно корреляционных значениях Е';

о, ∆, □ – опытные точки; - теоретические кривые.
Таблица 7.1
Сопоставление опытных и теоретических (опытно-корреляционных) значений продольных
относительных деформаций ε, секущего модуля деформаций E’, касательного модуля
деформаций Е и коэффициента упругости бетона ν
Опытные величины (по показаниям приборов) |
Теоретические величины (корреляционные) |
Отклнение теорети- ческих вел. от опыт. |
|||||||||||
σ, МПа |
|
ε 10-5 |
E’·10-4, МПа |
E·10-4, МПа |
ν |
ε 10-5 |
E’·10-4, МПа |
E·10-4, МПа |
ν |
∆ε % |
∆Е’, ∆ν % |
∆Е % |
|
0 |
0 |
0 |
- |
4,7347 |
1,0000 |
0 |
4,7347 |
4,7347 |
1,0000 |
0 |
0 |
0 |
|
2 |
0,062 |
4 |
5,0000 |
5,2802 |
1,0560 |
4,36 |
4,5901 |
4,4499 |
0,9695 |
+9,0 |
-8,2 |
-15,72 |
|
4 |
0,125 |
9 |
4,4444 |
4,1720 |
0,9387 |
9,00 |
4,4455 |
4,1740 |
0,9389 |
0 |
0 |
+0,05 |
|
6 |
0,187 |
14 |
4,2857 |
3,8793 |
0,9052 |
13,95 |
4,3010 |
3,9070 |
0,9084 |
-0,4 |
+0,4 |
+0,71 |
|
8 |
0,250 |
20 |
4,0000 |
3,3793 |
0,8448 |
19,25 |
4,1554 |
3,6487 |
0,8779 |
-3,75 |
+3,9 |
+7,97 |
|
10 |
0,313 |
26 |
3,8462 |
3,1244 |
0,8123 |
24,93 |
4,0118 |
3,3993 |
0,8473 |
-4,1 |
+4,3 |
+8,80 |
|
12 |
0,375 |
32 |
3,7500 |
2,9701 |
0,7920 |
31,03 |
3,8672 |
3,1586 |
0,8168 |
-3,0 |
+3,1 |
+6,35 |
|
14 |
0,438 |
38 |
3,6842 |
2,8668 |
0,7781 |
37,61 |
3,7226 |
2,9268 |
0,7862 |
-1,0 |
+1,0 |
+2,09 |
|
16 |
0,500 |
46 |
3,4783 |
2,5553 |
0,7346 |
44,72 |
3,5781 |
2,7040 |
0,7557 |
-2,8 |
+2,9 |
+5,82 |
|
18 |
0,562 |
53 |
3,3962 |
2,4361 |
0,7173 |
52,42 |
3,4335 |
2,4899 |
0,7252 |
-1,1 |
+0,9 |
+2,2 |
|
20 |
0,625 |
61 |
3,2787 |
2,2704 |
0,6925 |
60,81 |
3,2889 |
2,2846 |
0,6946 |
-0,3 |
+0,3 |
+0,63 |
|
22 |
0,687 |
70 |
3,1429 |
2,0863 |
0,6638 |
69,97 |
3,1443 |
2,0881 |
0,6641 |
-0,04 |
0 |
+0,09 |
|
24 |
0,750 |
79 |
3,0380 |
1,9493 |
0,6416 |
80,01 |
2,9997 |
1,9005 |
0,6336 |
+1,3 |
-1,2 |
-2,5 |
|
26 |
0,812 |
90 |
2,8889 |
1,7627 |
0,6102 |
91,06 |
2,8552 |
1,7218 |
0,6030 |
+1,2 |
-1,2 |
-2,32 |
|
28 |
0,875 |
101 |
2,7722 |
1,6231 |
0,5855 |
103,30 |
2,7106 |
1,5518 |
0,5725 |
+2,2 |
-2,3 |
-4,39 |
|
30 |
0,937 |
113 |
2,6549 |
1,3911 |
0,5420 |
116,91 |
2,5660 |
1,3907 |
0,5420 |
+3,5 |
0 |
-0,03 |
|
32 |
1,000 |
127 |
2,5197 |
1,3409 |
0,5322 |
132,15 |
2,4214 |
1,2383 |
0,5114 |
+4,1 |
-3,9 |
-7,63 |
|
Таблица 7.2