
- •4.1 Назначение и виды арматуры для железобетонных конструкций
- •4.2 Механические свойства арматурных сталей
- •4.3 Сварные арматурные изделия, стыки арматуры
- •Вопросы для самоконтроля по теме 4
- •Тема 7,8 Экспериментально-статистическая оценка модуля упругости и упруго-пластических характеристик бетона при кратковременном центральном сжатии методом линейного корреляционного анализа.
- •К вычислению коэффициента корреляции
Вопросы для самоконтроля по теме 4
1. Укажите назначения и виды арматуры для ЖБК.
2. Опишите механические свойства арматурных сталей.
3. Что такое дислокация и её движение в плоскости скольжения?
4. Как работает арматура в условиях повышенных температур?
5. Усталостное разрушение стали, в чем оно заключается?
6. Сварные арматурные изделия (сетки, каркасы).
7. Арматурные блоки, стыки сеток, неметаллическая арматура.
Тема 5
Основы теории вероятностей и математической статистки. События, случайные величины, ранжированный вариационный ряд. Гистограмма, полигон, кумулятивная кривая, медиана, мода. Дисперсионный, корреляционный и регрессионный анализ результатов измерений.
Нормы расчета и проектирования строительных конструкций построены с учетом статического анализа свойств материалов, геометрии сечений конструкций, действующих нагрузок и особенностей эксплуатации сооружений. Поэтому, когда по результатам испытаний прогнозируются эксплуатационные свойства строительных конструкций и сооружений, в качестве средства решения таких задач используют аппарат теории вероятностей и математической статистики.
Теория вероятностей изучает закономерности случайных событий. Событием считают любой факт, который может произойти или не произойти в результате опыта. Опытом в теории вероятностей называют осуществление определенного комплекса условий, которые реализуются многократно.
События бывают совместные и несовместные. Совместными являются такие события, когда одно из них сопровождается другим в одном и том же опыте. В противном случае события будут несовместными.
Достоверными считают событие, которое обязательно происходит в условиях данного опыта. Когда событие не может произойти, его называют невозможным. Если в опыте событие может произойти, а может и не произойти, оно называется возможным или случайным. При одинаковой степени появления событий их полагают равновозможными.
Количественной мерой объективной возможности случайного события А служит его вероятность Р(А). Вероятностью Р события А называют отношение числа случаев m, благоприятствующих появлению этого события, к общему числу n равновозможных событий:
Р(А) = m/n (5.1)
При Р(А) =0 событие невозможно, а при Р(А) =1 оно достоверно. Следовательно, вероятность Р(А) оценивается положительным числом, причем 0≤Р(А)≤1.
Относительная частота события (его статическая вероятность) определяется формулой Р*(А)= m/n,
где m- число испытаний, в которых появилось событие А. Здесь предполагается, что значение частоты стабилизируется лишь при достаточно большом числе опытов n. Таким образом, относительная частота события может служить приближенной оценкой его вероятности, точность определения которой повышается с увеличением числа опытов.
Основные теоремы теории вероятностей следующие. По теореме сложения- Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А+В)= Р(А) +Р(В) (5.2)
Доказательство. Введем обозначения: n- общее число возможных элементарных исходов испытания; m- число исходов, благоприятствующих событию А; m2- число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению события А, либо события В, равно m1+m2. Следовательно,
Р(А+В)= (m1+m2)/n= m1/n+m2/n.
Приняв во внимание, что
m1/n= Р(А) и m2/n= Р(В), окончательно получим
Р(А+В)= Р(А) +Р(В).
Пример
В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение. Появление цветного шара означает появление либо красного, либо синего шара.
Вероятность появления красного шара (событие А)
Р(А)=10/30=1/3.
Вероятность появления красного шара (событие В)
Р(В)=5/30=1/6.
Событие А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.
Искомая вероятность
Р(А+В)= Р(А) +Р(В)=1/3+1/6=1/2.
Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предложении, что первое событие уже наступило:
Р(А·В)= Р(А) ·РА(В) (5.3)
Доказательство. По определению условной вероятности,
РА(В)= Р(АВ) /Р(А).
Отсюда Р(АВ)= Р(А) ·РА(В) (*)
Замечание: Применив формулу (*) к событию ВА, получим
Р(ВА)= Р(В) ·РВ(А),
или, поскольку событие ВА не отличается от события АВ,
Р(АВ)= Р(В) ·РВ(А) (**)
Сравнивая формулы (*) и (**), заключаем о справедливости равенства
Р(А)· РА(В)= Р(В) ·РВ(А) . (***)
Вероятность события А, которое может иметь место только при реализации одного из несовместных событий В1, В2, …Вi, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
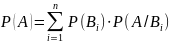 (5.4)
(5.4)
Выражение (5.4) носит название формулы полной вероятности.
Теорема сложения вероятностей совместных событий
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В)= Р(А) +Р(В)- Р(АВ). (5.5)
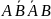 Доказательство.
Поскольку
события А и В, по условию, совместны, то
событие А+В наступит, если наступит одно
из следующих трех несовместимых событий
,
Доказательство.
Поскольку
события А и В, по условию, совместны, то
событие А+В наступит, если наступит одно
из следующих трех несовместимых событий
, 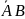 или АВ. По
теореме сложения вероятностей
несовместимых событий,
или АВ. По
теореме сложения вероятностей
несовместимых событий,
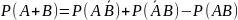 (*)
(*)
Событие А произойдет, если наступит одно из двух несовместных событий:
или АВ. По теореме сложения вероятностей несовместных событий имеем
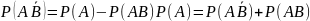
Отсюда (**)
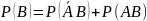 Аналогично
имеем
Аналогично
имеем

Отсюда (***)
Подставив
(**) и(***) в (*), окончательно получим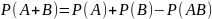
т.е. формула (5.5)
Случайной величиной Х называют такую величину, которая в процессе опыта принимает одно из возможных значений х1, х2, …, хn. Случайные величины могут быть дискретными или непрерывными. Дискретная случайная величина может быть задана перечислением всех её возможных значений (т.е. все её частные значения можно пронумеровать). Непрерывная случайная величина может принимать любые значения из некоторого конечного или бесконечного промежутка.
Совокупность частных значений одной случайной величины, полученных при измерениях, называют статистической совокупностью. Генеральная статистическая совокупность содержит все возможные значения случайной величины. В инженерной практике обычно имеют дело не со всей генеральной совокупностью, а только с некоторой её частью – выборочной статистической совокупностью. Для того чтобы по выборке можно было оценить генеральную совокупность, выборка должна воспроизводить характер генеральной совокупности или приближаться к ней. Таким образом методами математической статистики находят приближенные параметры распределения случайных величин с определенной погрешностью.
Статистическую совокупность значений переменной величины, расположенных в порядке их возрастания, называют ранжированным вариантным рядом (дискретным или непрерывным). Непрерывный вариационный ряд может быть заменен дискретным с шириной интервала.
h= (xmax- xmin)/k, (5.6)
где xmax, xmin – соответственно наибольшее и наименьшее значение величины в совокупности; k – число интервалов, принимаемое в пределах от 6 до 12.
Более точно ширина интервала определяется по формуле Стерджесса:
h= (xmax- xmin)/(1+3,32 lg n) (5.7)
 Отношение
частоты события ni
в пределах заданного интервала к общему
числу наблюдений
называют частостью:
Отношение
частоты события ni
в пределах заданного интервала к общему
числу наблюдений
называют частостью:
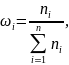 (5.8)
(5.8)
а отношение накопления частоты к общему числу наблюдений – накопленной или относительной частостью:
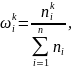
(5.9)
которая для последнего интервала наблюдений равна 1.
Для графического изображения вариационного ряда используют гистограмму, полигон или кумулятивную кривую, качественно характеризующие распределение случайной величины (рис 5.1).

Рисунок 5.1- Гистограмма (а), полигон (б), кумулятивная кривая (в), медиана и мода (г).
Закон распределения случайной величины устанавливает связь между возможными значениями случайной величины и соответствующими их вероятностями. Для решения многих практических задач достаточно определить несколько числовых характеристик, чтобы оценить наиболее существенные особенности распределения случайной величины. К таким характеристикам относят математическое ожидание, медиану, моду, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Математическое ожидание случайной величины
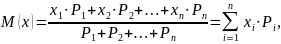
(5.10)
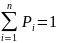 где
х1,
х2,
…, хn
– частные значения дискретной случайной
величины Х, которые она принимает с
вероятностью P1,P2,
…, Pn
,
где
х1,
х2,
…, хn
– частные значения дискретной случайной
величины Х, которые она принимает с
вероятностью P1,P2,
…, Pn
,
причем
Для непрерывной случайной величины
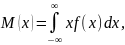 (5.11)
(5.11)
где f(x) – плотность вероятности случайной величины.
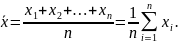 При
небольшом числе опытов математическое
ожидание заменяют средним арифметическим
исследуемой величины
При
небольшом числе опытов математическое
ожидание заменяют средним арифметическим
исследуемой величины
(5.12)
Медиана Ме случайной величины Х разделяет ранжированный ряд её значений на две равные по объему группы:
P(x<Me) = P(x>Me). (5.13)
Модой Мо случайной величины Х называют наиболее вероятное или такое её значение, которое наблюдалось наибольшее число раз.
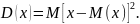 Дисперсия
случайной величины Х
– математическое ожидание квадрата
значения этой величины за вычетом её
математического ожидания:
Дисперсия
случайной величины Х
– математическое ожидание квадрата
значения этой величины за вычетом её
математического ожидания:
(5.14)
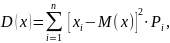 Дисперсия
дискретной случайной величины вычисляется
по формуле
Дисперсия
дискретной случайной величины вычисляется
по формуле
(5.15)
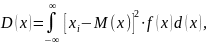 а
дисперсия непрерывной величины –
а
дисперсия непрерывной величины –
(5.16)
где n – число интервалов; Pi – вероятность попадания значения величины в i–й интервал.
Наглядной характеристикой рассеивания случайной величины около её математического ожидания является среднее квадратическое отклонение
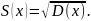 (5.17)
(5.17)
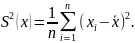 Дисперсию
для выборочной статистической
совокупности, найденную при ограниченном
числе опытов, определяют по формуле
Дисперсию
для выборочной статистической
совокупности, найденную при ограниченном
числе опытов, определяют по формуле
(5.18)
При ограниченной выборке используют несмещенную оценку дисперсии. Эта оценка не содержит систематической ошибки, поскольку в предварительных вычислениях учтено число степеней свободы f=n-1:
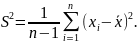 (5.19)
(5.19)
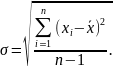 При
неограниченном возрастании числа
измерений (n→∞)
среднее квадратическое отклонение
стремится к своему истинному значению,
или стандарту
При
неограниченном возрастании числа
измерений (n→∞)
среднее квадратическое отклонение
стремится к своему истинному значению,
или стандарту
(5.20)
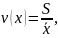 Отношение
среднего квадратического отклонения
случайной величины к среднему
арифметическому называют коэффициентом
вариации
Отношение
среднего квадратического отклонения
случайной величины к среднему
арифметическому называют коэффициентом
вариации
(5.21)
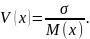 который
для генеральной совокупности определяют
как
который
для генеральной совокупности определяют
как
(5.22)
Дисперсионный, корреляционный и регрессионный анализ результатов измерений
В практике испытания конструкций зданий и сооружений применяют два основных способа накопления исходных статистических данных для последующей математической обработки: пассивный и активный эксперимент.
Эксперимент - это система операций, воздействий и наблюдений, направленных на получение информации об объекте при исследовательских испытаниях. Составной его частью является опыт – воспроизведение исследуемого явления в определенных условиях проведения эксперимента при возможности регистрации его результатов.
Пассивный эксперимент основан на регистрации экспериментальных данных в процессе испытаний строительных материалов, конструкций и сооружений при изменении внешней нагрузки по заданной программе. При этом анализируют возникающие в конструкции напряжения и её деформации.
Активный эксперимент проводят по специально разработанному плану. Однако переход к активному эксперименту возможен лишь тогда, когда накоплены в достаточном объеме исходные данные и имеется статистическая оценка разнообразных факторов, одновременно действующих на сооружение.
Выбрать наиболее важные независимые переменные и оценивать статистическими методами их влияние на исследуемую величину позволяет дисперсионный анализ. Если необходима оценка влияния только одной переменной, применяют однофакторный дисперсионный анализ, а при исследовании влияния двух или нескольких переменных – двух или многофакторный комплекс.
Дисперсионный анализ применим при взаимной независимости результатов измерений, подчиненных нормальному закону распределения, при линейной зависимости анализируемой величины от рассматриваемых факторов и тождественности дисперсий.
Методика однофакторного дисперсионного анализа состоит в следующем. Пусть в результате исследования определены m совокупностей значений независимой величины Х, причем в каждой группе опытов получена выборка объемом n. Каждая группа результатов измерений рассматривается как выборка из генеральной их совокупности, в которой каждый результат обозначается xij, где i – номер опыта (i=1,2, …, n). Такую выборку можно представить в виде матрицы (табл. 5.1).
Таблица 5.1- Матрица наблюдаемых значений величины Х
i |
Номер уровня независимой переменной фактора - j |
|||
1 |
2 |
… |
n |
|
1 |
X11 |
X12 |
… |
X1n |
2 |
X21 |
X22 |
… |
X2n |
… |
… |
… |
… |
… |
Среднее арифметическое результатов каждой группы измерений
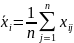
(5.23)
Общее среднее арифметическое результатов всех измерений
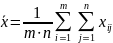 (5.24)
(5.24)
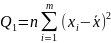 Рассеивание
результатов наблюдений оценивается
величиной
Рассеивание
результатов наблюдений оценивается
величиной
(5.25)
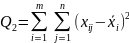 Сумма
квадратов отклонений результатов группы
опытов
Сумма
квадратов отклонений результатов группы
опытов
(5.26)
Полная сумма квадратов отклонений
Q=Q1+Q2 (5.27)
Обработку результатов дисперсностного анализа ведут в табличной форме (табл. 5.2)
Таблица 5.2- Однофакторный комплекс
Дисперсия результатов измерений |
Сумма квадратов отклонений |
Число степеней свободы |
Средние квадраты отклонений |
Межгрупповая |
Q1 |
m-1 |
Q1/ (m-1) |
Внутригрупповая |
Q1 |
m(n-1) |
Q2/ (m(n-1)) |
Полная |
Q1 +Q2 |
mn-1 |
Q/ (mn-1) |
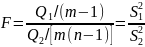 Оценку
различия межгрупповой и внутригрупповой
дисперсии производят по F-
критерию Фишера-Снедекора:
Оценку
различия межгрупповой и внутригрупповой
дисперсии производят по F-
критерию Фишера-Снедекора:
(5.28)
В зависимости от числа степеней свободы k1=m-1, k2=m(n-1) и уровня значимости q можно определить критерий Fq. Если F≤ Fq , гипотезу о равенстве дисперсий считают подтвержденной, в противном случае её отвергают.
Когда на результаты исследования влияют два или больше число факторов, методика вычислений остается такое же, как и при однофакторном анализе, но увеличивается их объем.
Зависимость между двумя переменными случайными величинами может быть функциональной или вероятностной. При их функциональной зависимости по значению одной величины находят строго определенное значение другой(рис. 5.2,а). При вероятностной зависимости, имеющей место в большинстве случаев на практике, точное значение второй величины определить невозможно, можно установить лишь закон её распределения.
Зависимость между одной случайной величиной и условными средними значениями другой называют корреляционной зависимостью, которая характеризуется формой и теснотой связи (рис. 5.2, б, в). Такая зависимость характерна для случайных величин, распределенных по нормальному закону.
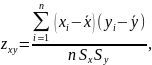 Наиболее
простой является линейная корреляционная
зависимость случайных величин X
и Y,
подчиняющихся нормальному закону
распределения, которая характеризуется
выборочным коэффициентом корреляции
Наиболее
простой является линейная корреляционная
зависимость случайных величин X
и Y,
подчиняющихся нормальному закону
распределения, которая характеризуется
выборочным коэффициентом корреляции
(5.29)
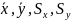 где
- средние
соответственно арифметические значения
величин X
и Y
и их квадратические отклонения,
определяемые по формулам (5.12) и (5.19).
где
- средние
соответственно арифметические значения
величин X
и Y
и их квадратические отклонения,
определяемые по формулам (5.12) и (5.19).
 Рисунок
5.2- Зависимость между случайными
величинами X
и Y:
Рисунок
5.2- Зависимость между случайными
величинами X
и Y:
а) –функциональная (|zxy|=1); б), в) – корреляционная(zxy>0); г) – величины не коррелированны (zxy=0); 1- линейная регрессия; 2-нелинейная регрессия.
Эмперические уравнения регрессии:
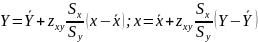 (5.30)
(5.30)
Выборочный коэффициент корреляции характеризует степень приближения зависимости между случайными величинами к линейной, если его значение находится в пределах -1≤ zxy ≤1. При zxy =0между случайными величинами X и Y корреляционная зависимость отсутствует или они не коррелируемы.(рис. 5.2,г), а при |zxy|=1 между ними имеется линейная функциональная связь (см. рис. 5.2,а). Если zxy=0,5, теснота связи считается удовлетворительной, а если zxy=0,8-0,89 – хорошей.
В общем случае связь между X и Y не линейная и выражается степенной, показательной или другой функцией распределения. Если случайная величина зависит не от одной, а от нескольких случайных величин, то при линейной связи между величинами используют частный, совокупный коэффициент корреляции или коэффициент корреляции рангов. Ввиду большой трудоемкости соответствующие расчеты рекомендуется выполнять на ПЭВМ.
Тема 6
Планирование экспериментальных исследований. Уровень фактора, поверхность отклика, область планирования. Математическая модель эксперимента. Матрица планов экспериментальных исследований. Звездные точки, области экспериментирования.
Планирование эксперимента позволяет ускорить исследования, улучшить их качество и уменьшить трудоемкость. Его сущность состоит в выборе плана, удовлетворяющего заданным требованиям от начального до заключительных этапов изучения объекта исследования и реализуемого в условиях неполного знания механизма изучаемого явления.
План эксперимента – совокупность данных, определяющих число, условия и порядок реализации опытов.
Фактор в теории планирования эксперимента – переменная величина, влияющая на его результаты. Для строительных конструкций это размеры сечений элементов, характеристики материалов и др.
Уровень фактора – фиксированное значение фактора относительно начала отсчета. Различают максимальный, минимальный и основной уровни факторов.
Наблюдаемую случайную переменную, зависящую от выбранных факторов называют откликом. Геометрическое представление функции отклика – поверхность отклика.
Часть факторного пространства, в котором находятся опытные точки, является областью планирования.
До проведения опытов отбирают факторы, оказывающие по предположению основное влияние на результат эксперимента. Уровни отображенных факторов должны быть детерминированы, совместимыми и некоррелированными.
При большом числе факторов проводится их ранжирование по степени значимости, чтобы обоснованно отбросить несуществующие из них. Варьирование факторов обычно ведут на двух уровнях – верхнем (с кодовым обозначением +1) и нижнем (-1) – или на трех – верхнем (+1), среднем (0) и нижнем (-1). Для упрощения записи единица может опускаться.
Математическая модель эксперимента записывается в виде функции:
Y =f(x1, x2, …, xn), (6.1)
где Y – отклик; x1, x2, …, xn – факторы.
Функцию (6.1) представляют в виде степенного ряда, коэффициенты которого определяют экспериментально:
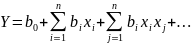 (6.2)
(6.2)
В двухфакторном эксперименте уровни факторов x1 и x2 варьируют на двух уровнях: максимальном (+1) и минимальном (-1). Интервалы варьирования ∆x1=xi max-xi min выбирают так, что они не превышают удвоенной среднеквадратической ошибки измерения уровня i-го фактора.
Используют скользящую систему координат, начало которой совпадает с нулевым уровнем факторов
Xi0=(xi max-xi min)/2. (6.3)
Нормализацию факторов – преобразование натуральных их уровней в безразмерные – проводят по формуле
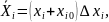 (6.4)
(6.4)
где xi – натуральное значение факторов; xi – натуральное значение фактора, соответствующее его основному уровню; ∆xi – интервал варьирования.
Для двухфакторного эксперимента все возможные комбинации будут исчерпаны четырьмя опытами (табл. 6.1).
Если оптимизируемая функция описывается линейным полиномом
Y=b0+b1x1+b2x2+b12x1 x2 (6.5)
 Коэффициенты
регрессии определяют по формулам
Коэффициенты
регрессии определяют по формулам
(6.6)
Таблица 6.1-Матрица плана эксперимента типа 22
Номер опыта |
х0 |
х1 |
х2 |
х1 х2 |
Yi |
1 |
+1 |
-1 |
-1 |
+1 |
|
2 |
+1 |
+1 |
-1 |
-1 |
|
3 |
+1 |
+1 |
-1 |
-1 |
|
4 |
+1 |
+1 |
+1 |
+1 |
|
Коэффициент регрессии значим и им пренебрегать нельзя, если
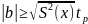 ,
(6.7)
,
(6.7)
где S2(X) – дисперсия коэффициента регрессии; tp – коэффициент Стьюдента, соответствующий заданной доверительной вероятности и числу степеней свободы, принятым при определении коэффициента регрессии.
Приемлемость линейного уравнения регрессии проверяют по критерию Фишера-Снедекора. Если результаты опытов с линейной моделью не согласуются, принимают модель второго порядка
Y=b0+b1x1+b2x2+b12x1 x2+b11x12+b22x22, (6.8)
п роводят
5-й опыт в центре плана (при Х1=Х2=0)
и опыты в звездных точках 6-9 (табл. 6.2).
На рис. 6.1 условия эксперимента представлены
геометрически в виде квадрата, номера
вершин которого соответствуют номерам
опытов, а площадь квадрата – области
экспериментирования.
роводят
5-й опыт в центре плана (при Х1=Х2=0)
и опыты в звездных точках 6-9 (табл. 6.2).
На рис. 6.1 условия эксперимента представлены
геометрически в виде квадрата, номера
вершин которого соответствуют номерам
опытов, а площадь квадрата – области
экспериментирования.
Рисунок 6.1- Геометрическое изображение полного факторного плана эксперимента типа 22
Номер опыта |
х0 |
х1 |
х2 |
х1 х2 |
Yi |
1 |
+1 |
-1 |
-1 |
+1 |
Y1 |
2 |
+1 |
+1 |
-1 |
-1 |
Y2 |
3 |
+1 |
-1 |
+1 |
-1 |
Y3 |
4 |
+1 |
+1 |
+1 |
+1 |
Y4 |
5 |
+1 |
0 |
0 |
0 |
Y5 |
6 |
+1 |
0 |
+1 |
0 |
Y6 |
7 |
+1 |
0 |
-1 |
0 |
Y7 |
8 |
+1 |
+1 |
0 |
0 |
Y8 |
9 |
+1 |
-1 |
0 |
0 |
Y9 |
Таблица 6.2- Матрица плана двухфакторного эксперимента
Матрицу плана для трех факторов, варьируемых на двух уровнях, получают из матрицы плана эксперимента для двух факторов, повторяя ее при значениях третьего фактора, заданного сначала на нижнем, а затем на верхнем уровне. Аналогично поступают при большем числе факторов, как это показано в табл. 6.3.
Таблица 6.3-Матрицы планов эксперимента для 2, 3, 4..5 факторов.
Номер опыта |
х0 |
х1 |
х2 |
х3 |
х4 |
х5 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
2 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
3 |
+1 |
-1 |
+1 |
-1 |
-1 |
-1 |
4 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
5 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
6 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
7 |
+1 |
-1 |
+1 |
+1 |
-1 |
-1 |
8 |
+1 |
+1 |
+1 |
+1 |
-1 |
-1 |
9 |
+1 |
-1 |
-1 |
-1 |
+1 |
-1 |
10 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
11 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
12 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
13 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
14 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
15 |
+1 |
-1 |
+1 |
+1 |
+1 |
-1 |
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
-1 |
17 |
+1 |
-1 |
-1 |
-1 |
-1 |
+1 |
18 |
+1 |
+1 |
-1 |
-1 |
-1 |
+1 |
19 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
20 |
+1 |
+1 |
+1 |
-1 |
-1 |
+1 |
21 |
+1 |
-1 |
-1 |
+1 |
-1 |
+1 |
22 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
23 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
24 |
+1 |
+1 |
+1 |
+1 |
-1 |
+1 |
25 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
26 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
27 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
28 |
+1 |
+1 |
+1 |
-1 |
+1 |
+1 |
29 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
30 |
+1 |
+1 |
-1 |
+1 |
+1 |
+1 |
31 |
+1 |
-1 |
+1 |
+1 |
+1 |
+1 |
32 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
С увеличением числа факторов реализация полного факторного плана эксперимента затрудняется ввиду значительного возрастания числа опытов. Например, при трех факторах необходимо провести 23=8 опытов, при четырех – 24=16, а при десяти 210=1024. Для сокращения числа опытов (кроме ранжирования факторов по степени значимости , о чем сказано выше) пользуются дробными репликами полного факторного плана, которые получают делением числа опытов в последнем на число, кратное двум. Так, при шести факторах потребуется проведение 26=64 опытов, полуреплика содержит вдвое меньше количество опытов – 26-1=32, а четверть реплика – в четыре раза меньше, т.е. 26-2=16.
Дробный факторный план позволяет получать регрессионные модели при меньшем числе опытов. Например, если на основании проведенного анализа установлено, что к существенным факторам относятся х0, х1, х2 и х3,но основными являются х1 и х2, а х3 зависит от взаимодействия двух первых факторов (х1х2), матрица полуреплики 23-1 будет соответствовать выделенной рамкой в табл. 6.3.
Процесс поиска адекватной математической модели обычно разбивают на несколько этапов. Вначале выполняют небольшую серию опытов для описания функции отклика полиномом первой степени. Если линейного приближения недостаточно, в следующей серии опытов движение к оптимуму осуществляется по кратчайшему пути. Процесс продолжают до тех пор, пока результаты не окажутся в области оптимума (рис. 6.2).

Рисунок 6.2- Движение по градиенту при активном эксперименте.
Пример Требуется рассчитать состав мелкозернистого бетона, соответствующего классу С 20/25 (В25) по прочности на сжатие и предназначенного для изготовления модели железобетонной рамы, при следующих исходных данных: портландцемент марки 400, модуль крупности песка Мкр=2,68, относительная влажность песка W=3,7%; условия твердения бетона – пропаривание по режиму 2+8+2 при t =80°С.
Основными факторами, влияющими на предел прочности бетона при сжатии, являются водоцементное отношение В/Ц (х1), относительное содержание в растворе песка П/Ц (х2). На основании предварительных опытов приняты основные уровни х1 и х2 (табл. 6.4). Нормализация факторов выполняется по формуле (6.4):
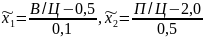
Таблица 6.4- Варьирование уровней факторов.
Характеристика |
В/Ц |
x1 |
П/Ц |
х2 |
Основной уровень |
0,5 |
0 |
2,0 |
0 |
Интервал варьирования |
0,1 |
- |
0,5 |
- |
Верхний уровень |
0,6 |
1 |
2,5 |
1 |
Нижний уровень |
0,4 |
-1 |
1,5 |
-1 |
Для изготовления шести кубов с размером ребра 70,7 мм потребуется около 2,5 дм3 (литра) бетонной смеси для каждой серии (табл. 6.5).
Таблица 6.5- Состав мелкозернистого бетона.
Характеристика уровня факторов |
Уровни факторов |
Содержание компонентов в бетоне, кг |
Основной |
В/Ц=0,5; П/Ц=2,0 |
Песок-3,5; цемент- 1,75; вода- 0,87 |
Верхний |
В/Ц=0,6; П/Ц=2,5 |
Песок-3,7; цемент- 1,48; вода- 0,89 |
Нижний |
В/Ц=0,4; П/Ц=1,5 |
Песок-3,3; цемент- 2,2; вода- 0,88 |
Промежуточный |
В/Ц=0,6; П/Ц=1,5 |
Песок-3,7; цемент- 2,47; вода- 1,48 |
То же |
В/Ц=0,4; П/Ц=2,5 |
Песок-3,4; цемент- 1,36; вода- 0,54 |
Допустим, что оптимизируемая функция описывается полиномом первой степени (6.5). Коэффициенты полинома определены по формулам (6.6) и получено уравнение
Yр=18,5-6,5x1-3x2+4x1 x2, (6.9)
которое согласуется с результатами опытов (табл. 6.6). Всего испытано 30 кубов.
Таблица 6.6- Матрица плана эксперимента.
Номер опыта |
x1 |
x2 |
В/Ц |
П/Ц |
Yэ |
Yр |
∆Y |
1 |
-1 |
-1 |
0,4 |
1,5 |
32,0 |
32,0 |
- |
2 |
+1 |
-1 |
0,6 |
1,5 |
14,0 |
14,0 |
- |
3 |
-1 |
+1 |
0,4 |
2,5 |
18,0 |
18,0 |
- |
4 |
+1 |
+1 |
0,6 |
2,5 |
13,0 |
13,0 |
- |
5 |
0 |
0 |
0,5 |
2,0 |
17,5 |
18,5 |
1,0 |
В контрольном опыте при х1=0, х2=0 получено Уэ=17,5 МПа, что на 5,7% меньше, чем Ур=18,5 МПа. Следовательно, искомая зависимость с достаточной для практических расчетов точностью может быть описана полиномом первой степени.
Уравнение (6.9) можно записать с заданными соотношениями В/Ц и П/Ц
Rb=138-215В/Ц-46П/Ц+80В/Ц·П/Ц (6.10)
По уравнению (6.10) можно рассчитать состав бетона по заданной его прочности к моменту испытания модели.
