Пп. 3. Метод обратной матрицы
(для решения неоднородных систем,
когда
)
,
матричная запись системы имеет вид
 .
.
Если А – невырожденная матрица ( ),
то для нее существует обратная матрица
),
то для нее существует обратная матрица
 (по
теореме):
(по
теореме):
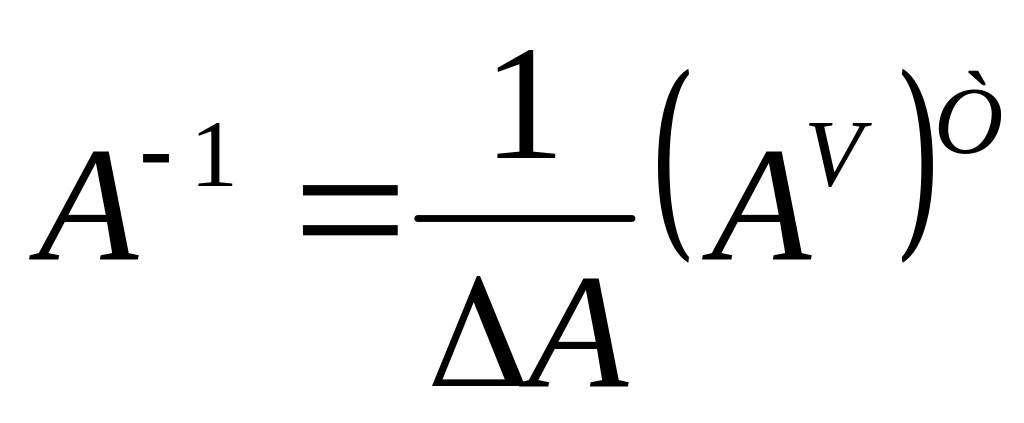 .
.
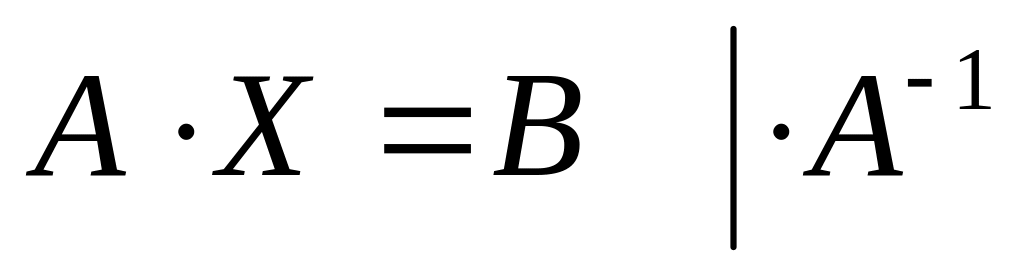 обе
части, получим
обе
части, получим
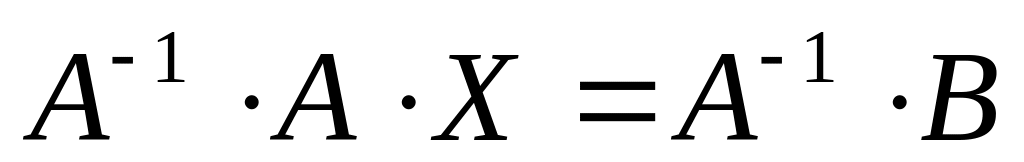 ,
,
отсюда
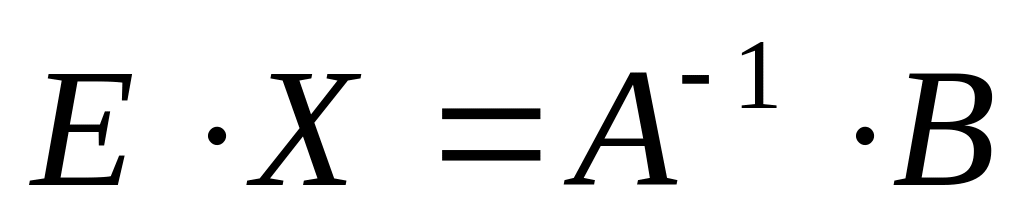 ,
т.е.
,
т.е.

 - матрица-столбец неизвестных.
- матрица-столбец неизвестных.
Пример. Решить систему уравнений:
.
Решение. Матрица системы
 ,
столбец свободных членов
,
столбец свободных членов
 ,
столбец неизвестных
,
столбец неизвестных
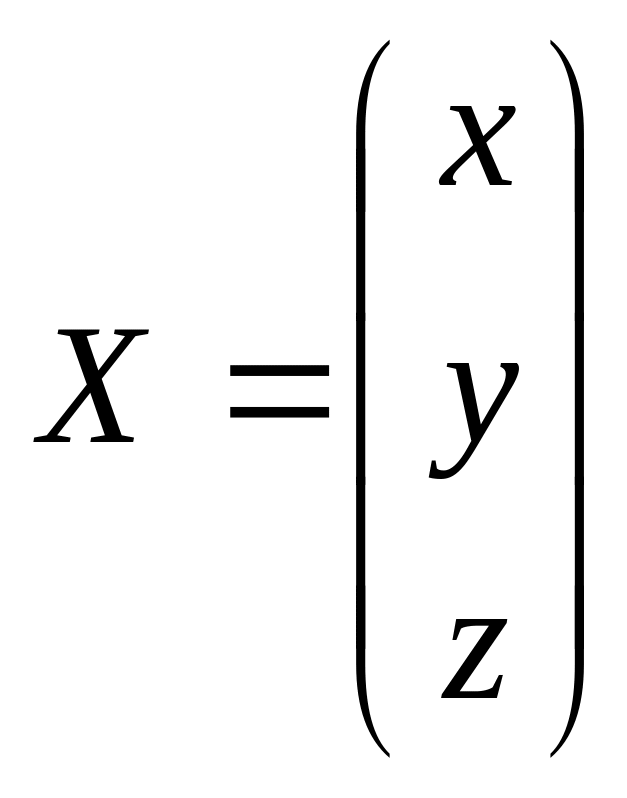 .
Найдем определитель матрицы системы:
.
Найдем определитель матрицы системы:
 ,
следовательно, существует обратная
матрица
.
,
следовательно, существует обратная
матрица
.
Найдем алгебраические дополнения:
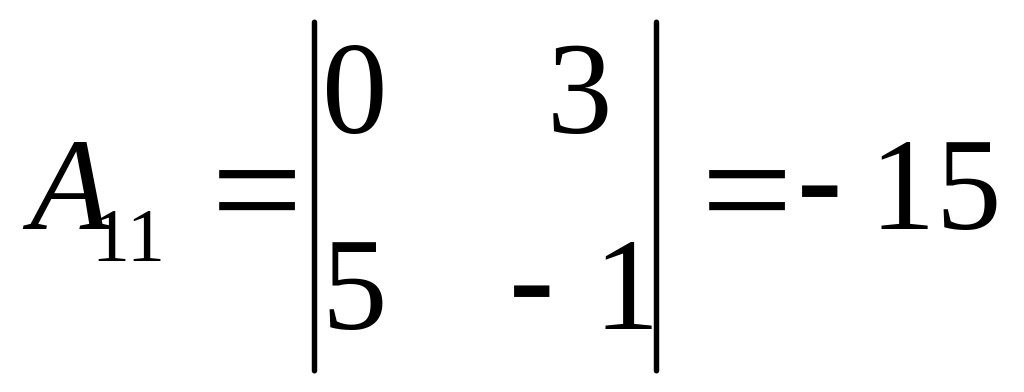 ,
,
 ,
,
 ,
,
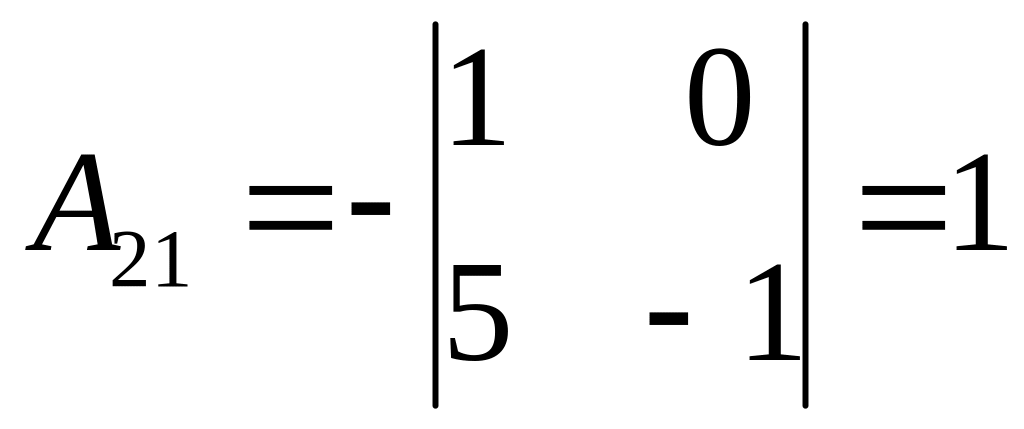 ,
,
 ,
,
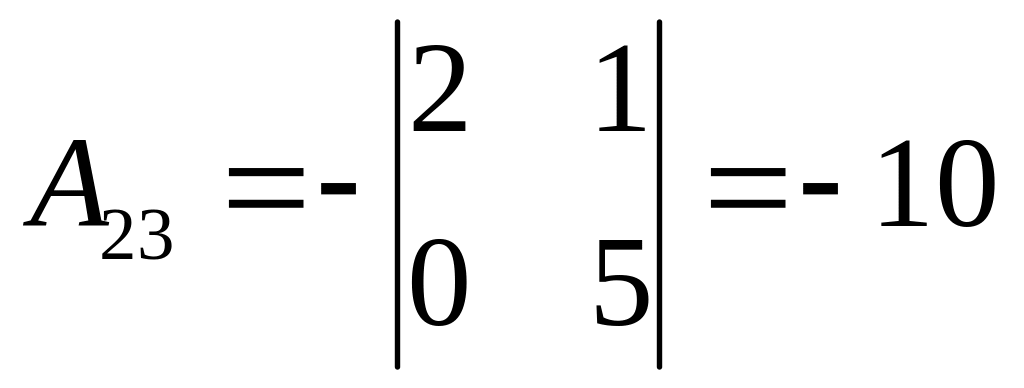 ,
,
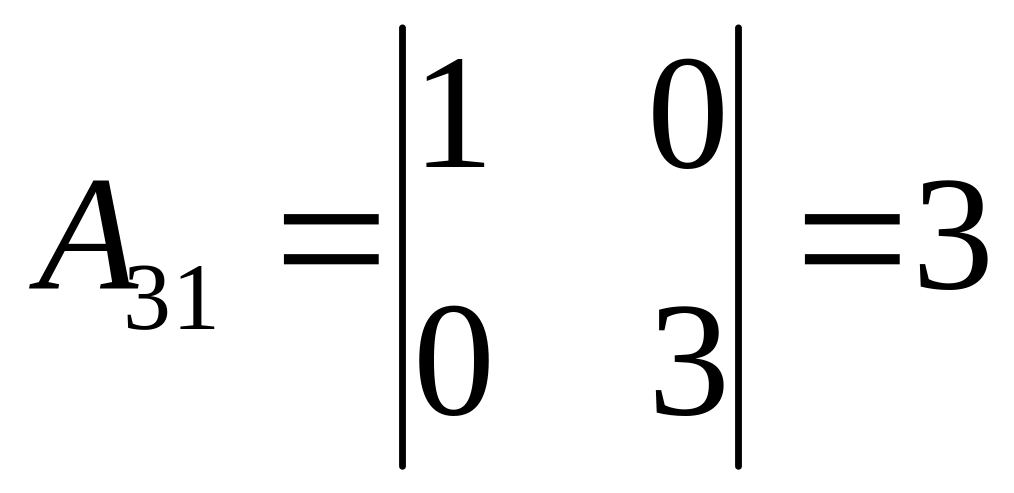 ,
,
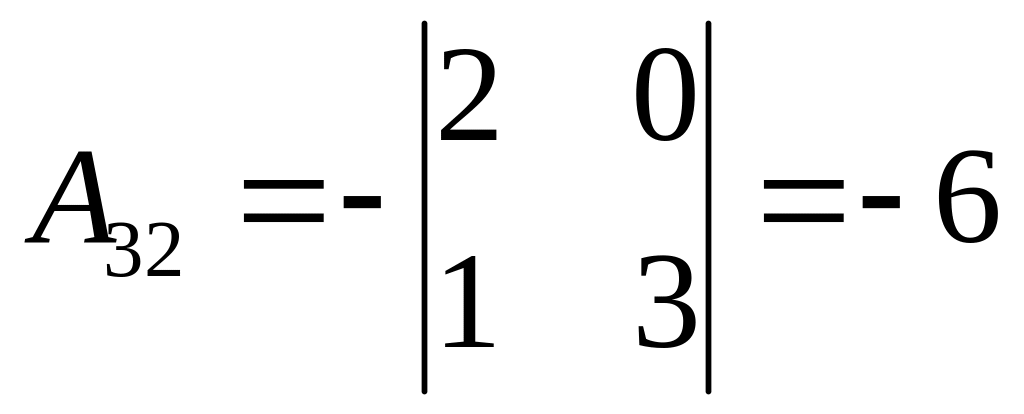 ,
,
 .
.
Запишем присоединенную транспонированную
матрицу
 ,
тогда обратная матрица имеет вид:
,
тогда обратная матрица имеет вид:
 .
.
Найдем матрицу-столбец неизвестных:
 .
Отсюда, x = 1, y
= 3, z = 5.
.
Отсюда, x = 1, y
= 3, z = 5.
Ответ: {(1, 3, 5)}.


 - матрица-столбец неизвестных.
- матрица-столбец неизвестных. ,
столбец свободных членов
,
столбец свободных членов
 ,
столбец неизвестных
,
столбец неизвестных
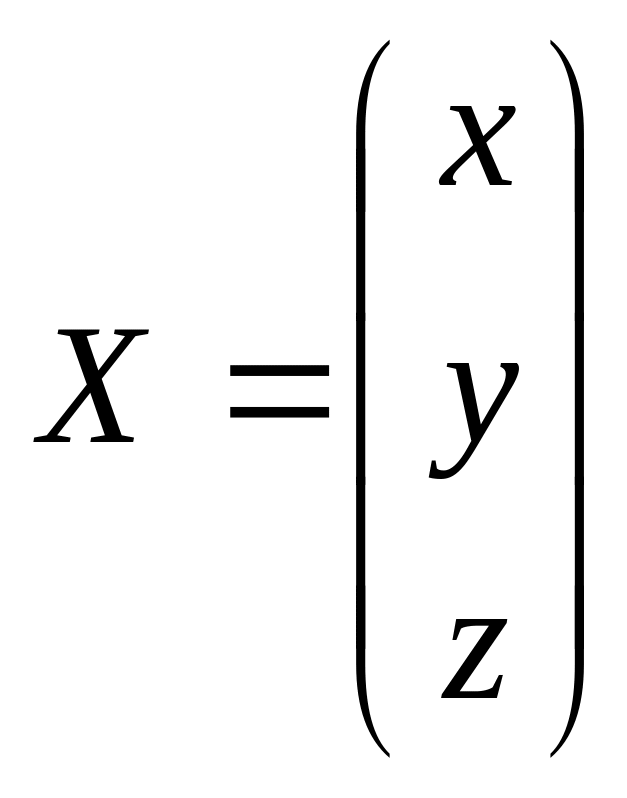 .
Найдем определитель матрицы системы:
.
Найдем определитель матрицы системы:
 ,
следовательно, существует обратная
матрица
.
,
следовательно, существует обратная
матрица
. ,
тогда обратная матрица имеет вид:
,
тогда обратная матрица имеет вид:
 .
. .
Отсюда, x = 1, y
= 3, z = 5.
.
Отсюда, x = 1, y
= 3, z = 5.