Контрольные вопросы

1. Какими статистическими методами исследуется однородность изучаемой совокупности?

2. Какие виды средних применяются в статистике?

3. Каковы основные свойства средней арифметической?

4. Для каких целей используется средняя гармоническая?

5. Как рассчитывается средняя геометрическая и в каких случаях она применяется?

6. Что представляет собой вариация признака, от чего зависят ее размеры?

7. Какие показатели характеризуют вариацию признака?

8. Что собой представляют моменты статистического распределения?

9. Какова методика определения статистических характеристик сложных процессов и явлений?

10. Какие основные задачи решают с помощью метода группировок и корреляционно‑регрессионного анализа?

11. Каковы основные проблемы и правила построения однофактор‑ной линейной регрессионной модели?

12. Какова экономическая интерпретация коэффициентов регрессии?

13. Какими показателями измеряется теснота связи?

14. Каковы основные проблемы и правила построения многофакторной корреляционной модели?

15. Какова последовательность изучения связей между экономическими явлениями?

Глава 2 целесообразность и последовательность применения статистических методов при анализе динамических процессов и явлений

2.1. Измерение тенденции изучаемых явлений и экстраполяция тренда

Все явления природы и общества, в том числе и экономические, изменяются и развиваются. Поэтому статистика не могла бы правильно характеризовать экономические явления, если бы она не изучала их в состоянии развития, в динамике. Развитие экономических явлений во времени называется динамическим развитием, а информация об этом развитии – динамическим рядом. Анализ динамических рядов экономических явлений может быть осуществлен по следующей схеме (рис. 3).

Одной из основных задач анализа динамических рядов экономических явлений и процессов является установление составляющих (компонентов), на которые можно разложить динамический ряд.

Большинство авторов выделяют наличие трех составляющих в динамическом ряду:

• тенденцию, выражаемую трендом;

• сезонные колебания;

• случайные колебания.

Каждая из этих составляющих вызвана определенными факторами. Так, тенденция объясняется наличием постоянных сил, вызывающих либо постоянный подъем, либо постоянное снижение, либо чередование того и другого.

Сезонные колебания формируются под воздействием периодических колебаний в течение года. Примером сезонных колебаний в динамическом ряду могут служить: увеличение производства продукции животноводства и использования трудовых ресурсов в сельском хозяйстве в летние месяцы года и их снижение в зимние месяцы. Более подробно о факторах, вызывающих сезонные колебания, и об их измерении будет сказано в пункте 2.3.

Если из динамического ряда вычесть эти составляющие, то останется колеблющийся ряд, который может представлять собой либо чисто случайные колебания, либо смесь случайных колебаний с неким плавным колебательным движением, представляющим собой долгопериодическую составляющую колеблемости (одной из причин которой могут быть циклы солнечной активности).

Такой подход к разложению динамического ряда предполагает, что он может быть представлен суммой соответствующих составляющих, т. е. детерминированной его части, выражающей тенденцию развития, и случайной составляющей, если в динамическом ряду отсутствуют периодические колебания.

Изучение динамического ряда начинается с выявления тенденции развития.

Методы расчета основной тенденции можно условно разделить на две группы. Первая группа методов носит название «механическое сглаживание», так как предполагает только выявление тенденции, не связанное с дальнейшим прогнозированием. Сюда можно отнести сглаживание ряда динамики путем укрупнения интервала и применения скользящей средней. Они просты в расчетах и достаточно наглядно представляют тенденцию развития изучаемого явления, но на их основе нельзя осуществить прогнозирование и, кроме того, к недостаткам следует отнести необоснованность выбора периода сглаживания.

Методика расчета рассмотрена на примере урожайности (табл. 16).

Простейшим методом выявления основной тенденции является метод укрупнения интервала, который позволяет в значительной степени абстрагироваться от случайных колебаний, так как рассчитываются средние уровни динамического ряда за более длительный период. В нашем примере рассчитаны 5‑летние средние урожайности как средние арифметические простые. В результате наглядно прослеживается тенденция роста урожайности, но вместо 29 уровней мы имеем всего лишь 6, т. е. теряем динамический ряд.

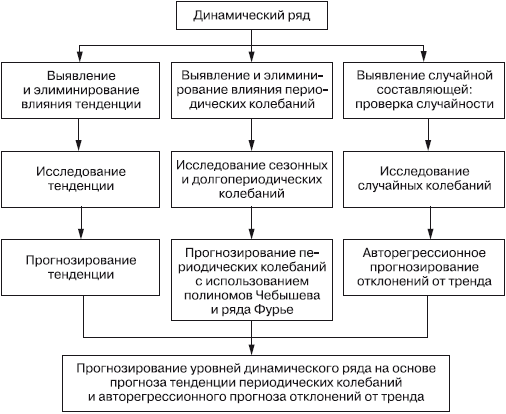
Рис. 3. Схема статистического изучения динамических рядов экономических явлений

Если же взять период укрупнения не 5 лет, а 11, с тем чтобы избежать влияния долгопериодических колебаний (а для этого динамический ряд должен быть достаточно длинным), то мы получим не более трех значений урожайности – 10,3; 13,6; 16,1 ц/га, которые также свидетельствуют о ярко выраженной тенденции роста урожайности. Кроме того, подобного рода средние (как за 5/летний период, так и за 11 лет) получены за изолированные периоды, а чтобы избежать этого и получить более длительный динамический ряд, рассматривают средние значения за укрупненный период, но с последовательным сдвигом на один год. Отсюда название: скользящие средние. Первое значение скользящей средней совпадает со средней, рассчитанной по методу укрупнения интервалов; второе будет получено как средняя арифметическая из пяти значений, но начиная со второго значения ряда; третье – начиная с третьего значения ряда, и т. д. Так же рассчитывается средняя скользящая и для других периодов. Полученные средние значения записываются в середине каждого интервала. Таким образом, мы будем иметь новый дополнительный ряд, состоящий из

Таблица 16. Выявление основной тенденции методом укрупнения интервалов и скользящих средних на примере урожайности зерновых культур

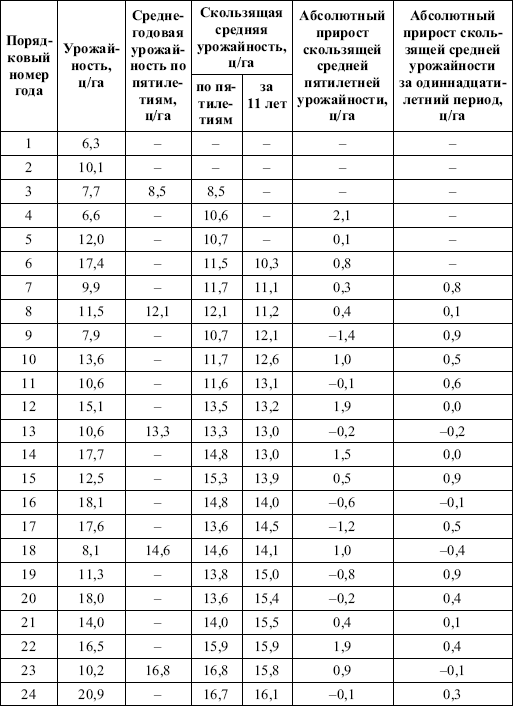
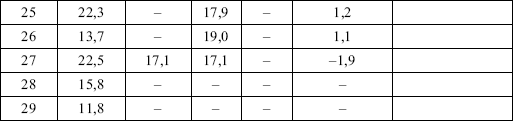
скользящих средних, но он короче первичного динамического ряда на k – 1 уровней, где k – число лет в интервале сглаживания. Новый дополнительный ряд в значительной степени лишен случайных колебаний, особенно наглядно это видно в динамическом ряду скользящих средних за укрупненный период. Такой ряд достаточно хорошо выявляет тенденцию изменения, но не дает возможности осуществить прогноз урожайности.

В основе другого типа методов выявления тенденции динамики лежит предположение, что ряд имеет определенную закономерность развития, которая может быть выявлена и описана тем или иным математическим выражением, т. е. уровень динамического ряда есть функция от времени f(t). Это методы аналитического выравнивания динамического ряда, основанные на методе наименьших квадратов. Основой для выбора тренда, описывающего тенденцию изменения, является прежде всего всесторонний анализ сущности изучаемого явления. Большую помощь при выборе типа линии может оказать графическое изображение первичного динамического ряда изучаемого явления. Однако этот способ не лишен субъективизма, особенно в тех динамических рядах, где наблюдаются сильные колебания. Выбор линии в значительной степени может зависеть от масштаба графического изображения.

В нашем примере (рис. 4) изображенный первичный динамический ряд урожайности позволяет предположить, что для выявления основной тенденции вполне может подойти прямая линия. Об этом же свидетельствуют данные средней скользящей урожайности, нанесенные на этом же графике.

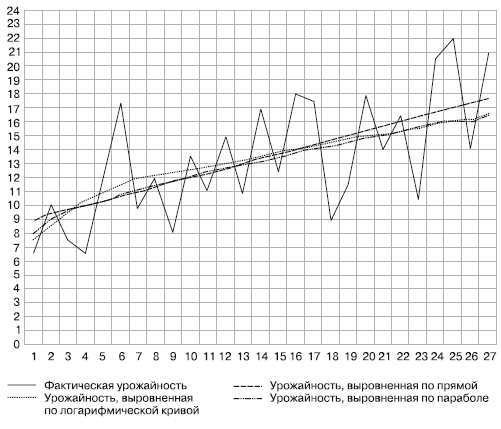
Рис. 4. Динамика урожайности зерновых культур

Для выравнивания динамических рядов применяются полиномы разных степеней, различного рода экспоненты и логистические кривые, однако аналитическое выравнивание чаще всего производится по уравнению прямой линии и параболой 2/го порядка, что экономически лучше интерпретируется. Остальные кривые, как правило, преобразовываются к виду линейной функции.

Существуют различные методики выбора типа выравнивающей линии, например, рекомендуют использовать метод последовательных разностей, в соответствии с которым цепным методом исчисляют разности уровней динамического ряда, а затем эти разности исследуют. Если приблизительно одинаковы первые разности, т. е. абсолютные приросты, то для выражения основной тенденции динамики можно использовать прямую линию. Если примерно постоянны вторые разности, т. е. разности абсолютных приростов, то используется парабола второго порядка. При постоянстве третьих разностей применяется парабола третьего порядка и т. д. Иначе говоря, порядок разностей принимается за степень полинома. Отсюда вытекает, что этот метод не является универсальным – он применим, только если изучаемое явление описывается уравнением многочлена.