1.4. Определение статистических характеристик сложных процессов или явлений

В ряде случаев представляет интерес отыскание статистических параметров среднего значения, дисперсии, коэффициента вариации, когда наблюдение за каким‑либо процессом или явлением представляет собой сложную функцию двух процессов. Например, вариация валового сбора зависит от вариации посевной площади и урожайности сельскохозяйственных культур; вариация молочного жира зависит от вариации количества молока и процента жира в молоке и т. д.

Рассмотрим пример, когда процесс представляет произведение двух переменных.

Пусть Y = X₁X₂, причем у процессов X₁ и X₂ известны следующие параметры: X₁ и X₂ – средние значения; σ1 и σ2  – средние квадратические отклонения; V₁ и V₂ – коэффициенты вариации.

Необходимо определить аналогичные параметры сложного процесса (Y), используя уже известные параметры.

Сложный процесс можно представить таким образом:

Y = X₁X₂ = (X₁ +ΔX₁)(X₂ +ΔX₂) = X₁X₂ +X₂ΔX₁ +ΔX₁X₂ +ΔX_1ΔX₂.

После усреднения найдем, что:

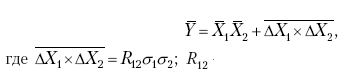
– коэффициент парной корреляции между X₁ и X₂, о котором речь пойдет дальше. 11,24/268,82 = 0,0418, или 4,18.

Тогда Y = X₁X₂ + R₁₂σ1σ2.

Вынося за скобки X₁X₂, получим:

Y = X₁X₂ (1 + R₁₂V₁V₂). (1.22)

Дисперсию σ_y² найдем из выражения:

σ_y² = Y² – (Y)².

Подставив вместо Y его выражение через X₁ и X₂, после несложных преобразований получим:

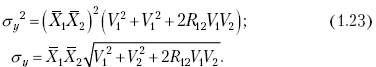
Тогда коэффициент вариации будет равен:

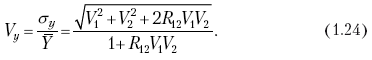
Рассмотрим на конкретном примере (табл. 6).

Исходя из данной информации, определяем статистические параметры исследуемых явлений обычным способом:

X₁ = 6689,7 кг; X₂ = 4,038 %; Y = 268,95 кг;

Таблица 6. Данные об удое коров, жирности молока и количестве молочного жира

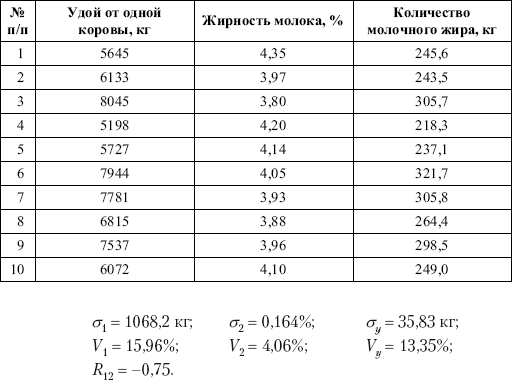
А теперь проверим предложенную методику и рассчитаем (Y₁, σ_y,V_y), исходя из известных данных X₁ и X₂ и неизвестной информации по Y. В нашем примере известными будем считать все статистические характеристики удоя молока и содержания жира в молоке; при этом ничего не известно о количестве молочного жира. Но так как количество молочного жира будет равно количеству молока, умноженному на содержание жира в молоке (например 5645×0,0435 = 245,6), то, используя вышеизложенную методику, определяем:

Сравнивая рассчитанные по данной методике характеристики с представленными ранее результатами, видим, что результаты получились одинаковые, т. е. в пределах допустимой статистической погрешности.

Так, например, ошибка средней величины составляет:

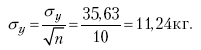
В относительном выражении она будет равна всего лишь:

11,24/268,82 = 0,0418, или 4,18 %.

Так же можно рассчитать погрешности и для других параметров. Рассмотрим случай, когда изучаемое явление представляет собой не произведение двух переменных, а частное, т. е.:

Также представляет интерес получить статистические характеристики сложного явления, состоящего из суммы или разности двух явлений.

В этом случае:

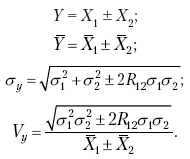
Рассмотрим на конкретном примере (табл. 7).

Таблица 7. Данные о рождаемости, смертности и естественном приросте в ряде стран на 1000 человек населения

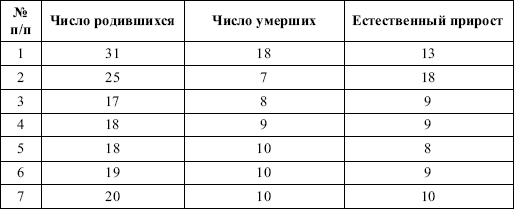
На основе данной информации имеем:

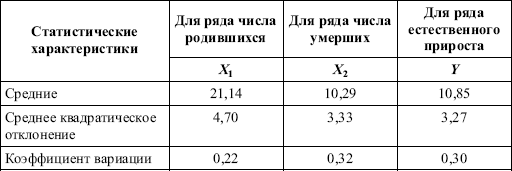
А теперь допустим, что никаких данных о естественном приросте нет, а известны статистические характеристики числа родившихся Х₁ и умерших Х₂ и известен коэффициент парной корреляции между ними, равный R = 0,722, рассчитанный по формуле:

Полученные характеристики полностью повторяют рассчитанные ранее другим способом, т. е. по статистическому ряду естественного прироста.

Рассмотренные характеристики вариационных рядов, по которым можно судить о центральной тенденции, о вариации сложных явлений, служат важным орудием в статистическом анализе. Взаимосвязанное их использование помогает более детально изучить особенности и закономерности экономических явлений и процессов.