2.3. Полный заряд в полупроводнике при заданном поверхностном потенциале

Ограничимся рассмотрением приближения невырожденного электронного газа. Это приближение работает в режиме обеднения и слабой инверсии и вполне удовлетворительно описывает ситуацию сильной инверсии, соответствующую вырожденным носителям.

Одномерное уравнение Пуассона для объема полупроводника p-типа имеет вид:

. (2.3.1)

Нас интересует случай обеднения и инверсии, когда . С учетом (2.1.1) и пренебрегая концентрацией дырок, имеем следующее приближение для правой части уравнения Пуассона:

(2.3.2)

Используя переменную , имеющую смысл электрического поля, проинтегрируем обе стороны уравнения от границы раздела кремния с изолятором, где электрическое поле равно искомому полю , а потенциал равен поверхностному потенциалу , до границы обедненного слоя, где электрическое поле и потенциал равны нулю:

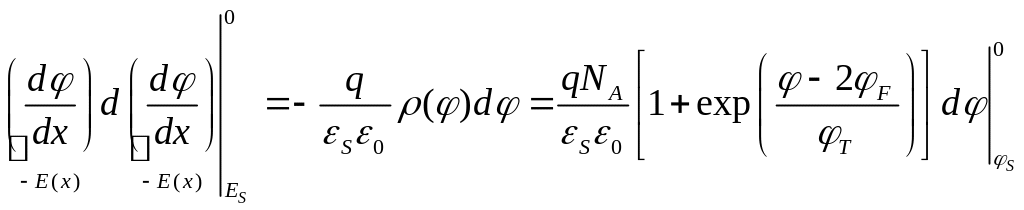(2.3.3)

Отсюда получаем связь электрического поля на границе раздела и поверхностного потенциала

, (2.3.4)

где введено обозначение для безразмерной функции

(2.3.5)

и для характерной длины задачи, которой является дебаева длина экранирования

. (2.3.6)

Тогда электрическое поле на границе раздела в кремнии

, (2.3.7)

а полная поверхностная (Кл/см^-2) плотность заряда в полупроводнике для заданного потенциала

. (2.3.8)

Предельные случаи сильной инверсии и глубокого обеднения:

(2.3.9)

В первом случае мы пренебрегли первым слагаемым в , ответственным за заряд неподвижных акцепторов, во втором − зарядом в инверсионном слое (канале).

2.4. Плотность электронов в канале как функция поверхностного потенциала

Поверхностная плотность заряда электронов в канале есть разность между полной плотностью заряда в полупроводнике и плотностью заряда обедненного слоя. Для поверхностной плотности электронов имеем:

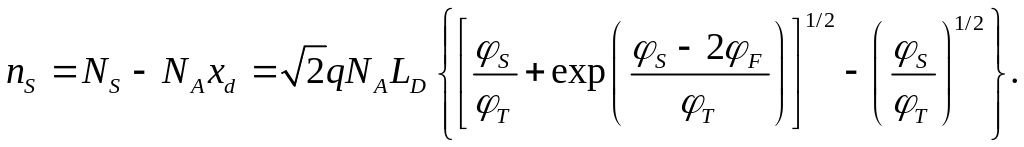(2.4.1)

Воспользовавшись алгебраическим тождеством , получаем выражение для поверхностной плотности электронов (см^-2) в канале как функции поверхностного потенциалa:

(2.4.2)

Полученная формула справедлива от глубокого обеднения до сильной инверсии. Плотность заряда электронов в канале (К/см²) в предельных случаях сильной инверсии и глубокого обеднения записывается в виде

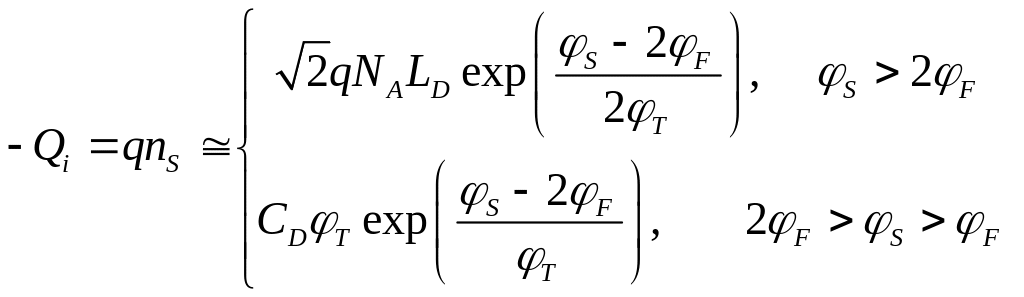, (2.4.3)

где удельная емкость обедненной области C_D (Ф/см²) определяется формулой (2.1.6). Формула (2.4.2) может быть использована для расчета зависимости .

Выразим поверхностную плотность заряда электронов в режиме сильной инверсии через концентрацию электронов на поверхности :

.(2.4.4)

Это позволяет найти эффективную толщину инверсного слоя , считая, что весь заряд находится в слое толщиной с объемной плотностью :

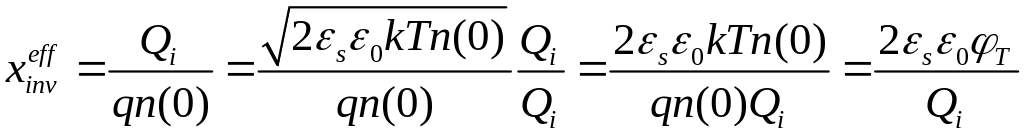(2.4.5)

Можно выразить поверхностную плотность заряда электронов в режиме сильной инверсии через эффективное электрическое поле в инверсном слое. Как будет показано в лекции 4, эффективное электрическое поле (4.4.1) равно

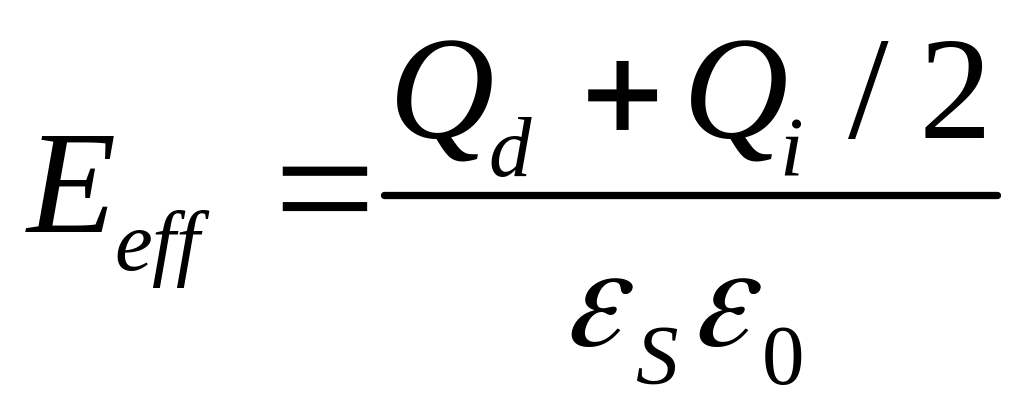
Полагая, что в режиме сильной инверсии , получаем . Подставляя в (2.4.5), получаем

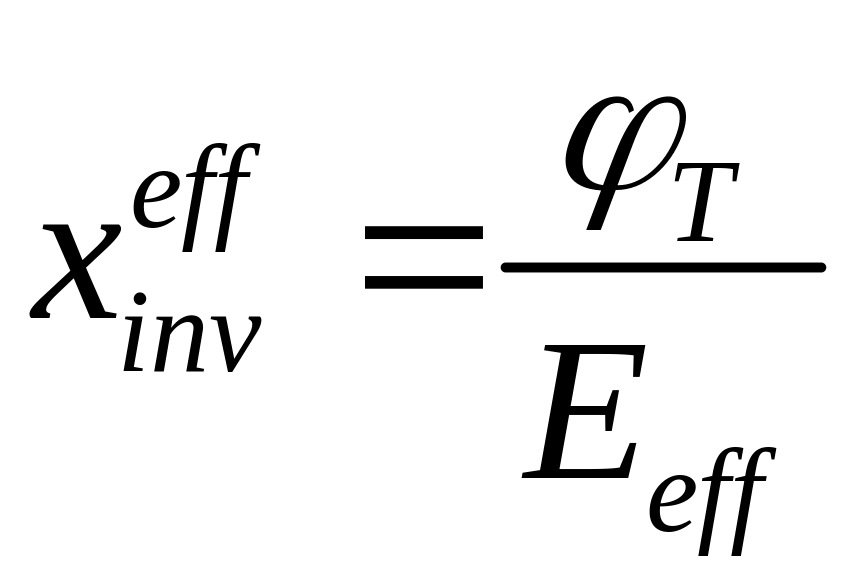(2.4.6).

Тогда 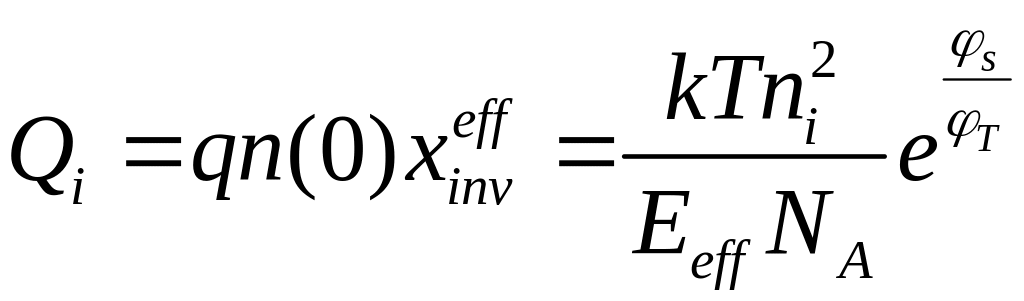(2.4.7).