2.2. Связь поверхностного потенциала с напряжением на затворе

Рассмотрим ситуацию, когда относительно подложки к затвору приложено положительное напряжение V_GB . Ток через структуру отсутствует, а разность уровней Ферми в затворе и подложке определяется приложенным напряжением:

. (2.2.1)

Плотность положительного заряда на затворе (К/см²) должна быть в точности равна плотности отрицательного заряда в полупроводнике (электроны инверсионного слоя плюс ионизированные акцепторы):

qN_G = q(n_s+N_Ax_d). (2.2.2)

Обратите внимание, что в выражении (2.2.2) N_G и n_s – не объемные, а поверхностные концентрации (см^-2)¹.

По закону Гаусса в окисле у границы раздела с металлом

. (2.2.3)

Если заряд в окисле отсутствует или расположен в тонком слое у границы раздела с кремнием (что является типичной ситуацией), то полное падение потенциала в окисле V_ox = E_oxd_ox. Полное падение потенциалов на толщине всей структуры складывается из падений потенциала в окисле V_ox и полупроводнике плюс контактная разность потенциалов:

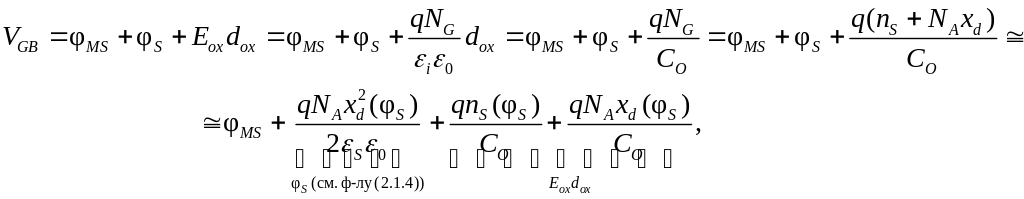(2.2.4)

где - удельная емкость окисла.

В неидеальной МОП структуре в окисле есть положительный заряд, захваченный на дефекты вблизи границы раздела Si-SiO₂ и вблизи неё (< 1 - 3нм). Дефекты такого рода могут обмениваться носителями с кремниевой подложкой, меняя свое зарядовое состояние. Заполнение и опустошение уровней дефектов контролируется их положением относительно положения уровня Ферми вблизи поверхности. Поэтому полный заряд на поверхностных и приповерхностных дефектах с поверхностной плотностью также зависит от поверхностного потенциала.

При наличии таких заряженных дефектов имеем и, соответственно, зависимость затворного напряжения от поверхностного потенциала приобретает вид:

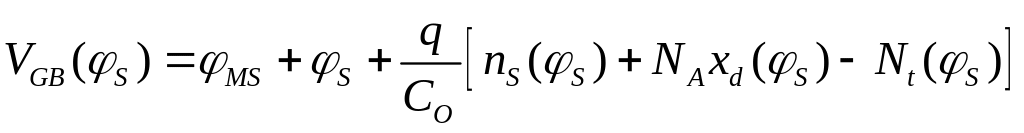(2.2.5)

В этом базовом уравнении все слагаемые (кроме ) в правой части являются функцией поверхностного потенциала. При малых напряжениях на затворе, когда в кремнии еще не сформировался инверсионный слой электронов, зависимость V_GB от поверхностного потенциала имеет почти линейный характер. Начало формирования инверсионного слоя (канала) сопровождается резким ростом функции , обусловленным экспоненциальной зависимостью плотности электронов в канале от поверхностного потенциала.

Пользуясь формулой (2.2.5), можно определить напряжение, при котором поверхностный потенциал в кремнии равен нулю. Его называют напряжением «плоских зон» V_FB (flatband voltage). Полный заряд в кремнии при этом равен нулю, и края зон кремния не изогнуты. Подставляя = 0 в (2.2.5), получаем

(2.2.6)

При некотором поверхностном потенциале объемная плотность неосновных носителей (электронов) на границе раздела сравнивается с плотностью основных носителей (дырок) в подложке: n( ) = N_A. Этот потенциал соответствует началу режима сильной инверсии

. (2.2.7)

Соответствующее напряжение, называемое пороговым напряжением, равно

. (2.2.8)

В (2.2.8) полагается, что при зарядом в инверсионном слое можно пренебречь.

При дальнейшем увеличении напряжения на затворе заряд в инверсионном слое экранирует объем полупроводника от проникновения электрического поля. Соответственно, перестает расти толщина обедненной области, насыщаясь на своем максимальном значении (2.1.7)

. (2.2.9)

Это очень важная величина, поскольку она определяет, например, минимально возможную длину канала. Наконец, замедление изменения поверхностного потенциала (следовательно, уровня Ферми на границе раздела) приводит к резкому уменьшению перезарядки приповерхностных дефектов в окисле. Это означает, что в формуле (2.2.5) в режиме сильной инверсии существенно изменяется только слагаемое, связанное с экспоненциальной функцией электронов в канале. С другой стороны, это слагаемое практически равно нулю при . Это дает возможность использовать в надпороговом режиме приближение для плотности электронов в канале, находящееся в очень хорошем согласии с экспериментальными данными,

. (2.2.10)

Рис. 2.3. Схематическая зависимость плотности носителей в канале от напряжения на затворе

Таким образом, при напряжении, превышающем пороговое хотя бы на несколько , плотность носителей в канале начинает расти практически линейно (см. рис. 2.3). Использование этого приближения позволяет обходить многие сложные расчетные проблемы.