Яф - 11 Аудиторные задачи

1.5 Динамика твердого тела Вариант 1

1. К точке, радиус-вектор которой относительно начала координат 0 равен , приложена сила , где а, b, А, В – постоянные, 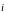и - орты осей х и у. Найти момент и плечо l силы 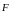относительно точки 0.

2. Тело массой m = 1,0 кг брошено из точки с координатами (0, 2, 0) (м) вверх по вертикали с начальной скоростью V₀ = 10,0 м/с. Найти приращение момента импульса 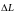относительно начала координат за все время полета тела (до возвращения в исходную точку). Ось Z направлена вверх. Сопротивлением воздуха пренебречь

3. Имеется тонкий однородный стержень массой m и длиной l. Найти его момент инерции относительно оси, проходящей через его центр и составляющей угол a со стержнем. Считать известным момент инерции материальной точки относительно оси.

4. Сплошной шар массой 1 кг и радиусом 0,05 м вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Угол поворота шара меняется по закону j = 2 + 2t — t². Определите величину действующей силы; тормозящий момент; время равнозамедленного движения.

5. 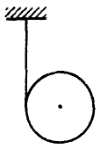Однородный цилиндр массой m = 8,0 кг и радиусом R = 1,3 см (см. рис.) в момент t = 0 начинает опускаться под действием силы тяжести . Найти угловое ускорение цилиндра и зависимость угла поворота от времени.

1.5 Динамика твердого тела Вариант 2

1. Сила 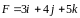приложена к точке, радиус-вектор которой . Найти: а) момент силы относительно начала координат; б) модуль вектора M; в) момент силы M_Z относительно оси Z.

2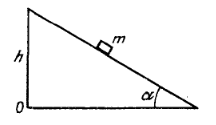 . Небольшая шайба массой m = 150 г начинает скользить с вершины гладкой наклонной плоскости, высота которой h = 100 см и угол наклона к горизонту a = 15⁰ (см. рис). Найти модуль момента импульса шайбы относительно оси 0, перпендикулярной плоскости рисунка, через t = 1,3 с после начала движения.

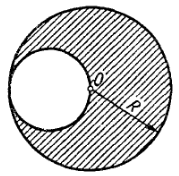
3. Однородный диск радиусом R имеет круглый вырез (см. рис) Масса оставшейся (заштрихованной) части диска равна m. Найти момент инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей через точку 0. Считать известным момент инерции сплошного диска.

4. Через неподвижный блок, представляющий собой сплошной диск радиусом г = 4 см и массой m = 0,2 кг, переброшена легкая нерастяжимая нить, на концах которой привязаны грузы массами m₁ = 0,3 кг и m₂ = 0,2 кг. При движении нить по блоку не скользит. Определите ускорение грузов; давление на ось блока.

5. С наклонной плоскости, составляющей с горизонтом угол a = 30⁰ , скатывается обруч. Длина наклонной плоскости l = 4 м . Найти скорость обруча в конце наклонной плоскости.

1.5 Динамика твердого тела Вариант 3

1 . Частице массой m сообщена начальная скорость под углом a к горизонту. Траектория полета частицы лежит в плоскости XY (см. рис). Пренебрегая сопротивлением воздуха, найти зависимость от времени относительно точки бросания момента силы, действующей на частицу.

2. Шарик массой m бросили под углом a к горизонту с начальной скоростью V₀. Найти модуль момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить в вершине траектории, если m = 130 г, a = 45⁰ и V₀ = 25м/с. Сопротивлением воздуха пренебречь.

3. Однородный диск радиусом R имеет круглый вырез (см. рис) Масса оставшейся (заштрихованной) части диска равна m. Найти момент инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр масс. Считать известным момент инерции сплошного диска

4 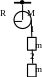. Однородный цилиндр массой М и радиусом R вращается без трения вокруг горизонтальной оси под действием двух грузов, подвешенных к легкой нити 1, намотанной на цилиндр, и связанных между собой легкой нитью 2 (см. рис). Масса каждого груза m. Определить натяжение нити 2.

5. С наклонной плоскости, составляющей с горизонтом угол a = 30⁰ , скатывается шар. Длина наклонной плоскости l = 4 м . Определить время скатывания шара с наклонной плоскости.