Яф - 11 Аудиторные задачи

1.3 Кинематика твердоготела Вариант 1

1. Точка движется по окружности со скоростью , где  = 0,5 м/с². Найти ее полное ускорение в момент, когда она пройдет n = 0,10 длины окружности после начала движения.

2.Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением , где b = 0,02 рад/с³. Через сколько времени тело совершит 800 оборотов.

3. Диск вращается с угловым ускорением  = - 2 рад/с². Сколько оборотов N сделает диск при изменении частоты вращения от n₁ = 240 мин ^-1 до n₂ = 90 мин ^-1? Найти время t, в течение которого это произойдет.

4. Точка А находится на ободе колеса радиуса R = 0,5 м, которое катится без скольжения по горизонтальной поверхности со скоростью V = 1,00 м/с. Найти модуль и направление ускорения точки А.

5. Горизонтальная платформа вращается с угловой скоростью 1 рад/с. По краю платформы идет человек. Определить угловую скорость человека относительно платформы и направление ее движения, если относительно земли он был неподвижен.

1.3 Кинематика твердоготела Вариант 2

1. Точка движется по окружности так, что зависимость пути от времени описывается уравнением 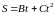, где В = -2 м/с, С = 2 м/с². Через t₁ = 1 с после начала движения нормальное ускорение точки a_n = 0,5 м/с². Найти время τ, при котором модули нормального и тангенциального ускорений будут равны.

2. Нормальное ускорение частицы, движущейся по окружности радиусом R = 3,2 м, изменяется по закону , где А = 2,5 м/с⁴. Найти путь, пройденный частицей за время τ = 5 с после начала движения.

3 . Колесо автомашины вращается равноускоренно. Сделав N = 50 полных оборотов, оно изменило частоту вращения от n₁ = 4 с ^-1 до n₂ = 6 с ^-1. Определить угловое ускорение  колеса.

4. Колесо радиуса R катится по горизонтальной поверхности без проскальзывания таким образом, что его ось О движется с постоянным ускорением а₀. Начальная скорость колеса равна нулю. Определить скорость и ускорение точки С колеса через время t после начала движения.

5. Два твердых тела вращаются вокруг неподвижных взаимно перпендикулярных пересекающихся осей с постоянными угловыми скоростями ₁ = 3,0 рад/с и ₂ = 4,0 рад/с. Найти угловую скорость и угловое ускорение одного тела относительно другого.

1.3 Кинематика твердоготела Вариант 3

1. Диск радиусом R = 20 см вращается согласно уравнению , где А = 3 рад, В = -1 рад/с, С = 0,1 рад/с³. Определить тангенциальное 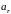, нормальное a_n и полное a ускорение точек на окружности диска для момента времени t = 10 c.

2. Твердое тело начинает вращаться вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота  по закону 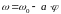, где ₀ и а – положительные постоянные. В момент t = 0 угол  = 0. Найти зависимость от времени: а) угла поворота; б) угловой скорости.

3. Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты вращения n = 300 мин ^-1. Определить угловое ускорение  маховика и число N оборотов, которое он сделал за это время.

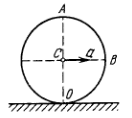
4. Шар радиуса R = 10,0 см катится без скольжения по горизонтальной плоскости так, что его центр движется с пос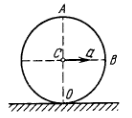 тоянным ускорением а = 2,50 см/с². Через t = 2,00 c его положение соответствует рисунку. Найти ускорения точек А и О.

5. По краю горизонтальной платформы, вращающейся равномерно в направлении вращения идет человек со скоростью 2 м/с относительно платформы. На какой угол повернется платформа за время за которое человек обойдет платформу, если угловая скорость платформы 2 рад/с, радиус платформы 5 м.