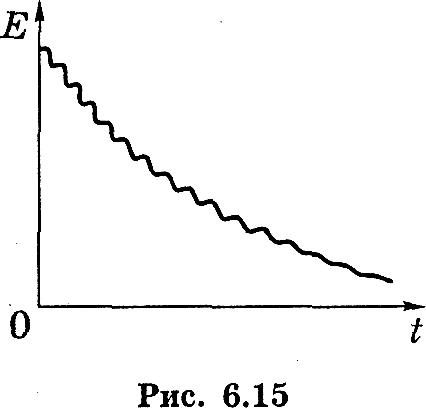
Энергия затухающих колебаний

Эта энергия складывается из потенциальной и кинетической: Ε = kx²/2 + т /2. После подстановки сюда выражений x(t) и (t), соответствующих затухающими колебаниям (7), получим зависимость E(t), которая графически показана на рис. 4. Уменьшение энергии колебаний обусловлено работой силы сопротивления. Мощность этой силы равна – r · = – r , тогда dE/dt = – r .

Т

Рисунок 4

аким образом, dE/dt < 0, кроме тех моментов, когда = 0. При малом затухании (β << ω₀) зависимость E(t) становится практически экспоненциальной:

, (10)

Отсюда убыль энергии в единицу времени

– dE/dt = 2βE. (11)

Характеристики затухания

Кроме коэффициента β затухание характеризуют и другими величинами:

1. Время релаксации τ — это время, за которое амплитуда колебаний уменьшается в е раз. Из выражения а = а₀е^-βt вид­но, что

τ=1/β. (12)

Интервал времени τ называют также постоянной времени осциллятора. Это оценка времени, в течение которого продолжается процесс свободных колебаний осциллятора, выведенного из положения равновесия. Разумеется, по истечении времени τ колебания продолжаются, но амплитуда, спадая по экспоненциальному закону, становится столь малой, что практически можно полагать, что колебания прекратились (скажем, через промежуток времени 5/β амплитуда падает более чем в 100 раз).

2. Логарифмический декремент затухания. Его определяют как

, (13)

где Т — период затухающих колебаний. λ показывает, на сколько изменяется амплитуда колебаний за 1 период. Например, при λ = 0,01 амплитуда ко­лебаний изменяется за 1 период приблизительно на 1%. Из предыдущих двух формул следует, что

λ=1/N_e, (14)

где N_e — число колебаний за время τ, в течение которого амп­литуда уменьшается в е раз.

При малом затухании (β << ω₀) λ характеризует относитель­ное уменьшение амплитуды колебаний за период. Это следует из (3.9), поскольку в этом случае

, (15)

Кроме того, при β << ω₀ относительное уменьшение энергии колебаний за период, согласно (3.7), равно δЕ/Е = 2βΤ = 2λ, откуда

λ=δЕ/2Е. (16)

3. Добротность осциллятора. По определению,

Q=π/λ=πN_e. (17)

Эту величину применяют для характеристики чувствительности колебательной системы к резонансным воздействиям.

При малом затухании (β << ω₀), когда справедливо (16),

Q≈2πΕ/δΕ. (18)

В заключение отметим, что анализ формулы (8) приводит к выводу: затухающие колебания возможны при условии β < ω₀ , а при достаточно большом затуха­нии (β ≥ ω₀) система совершает апериодическое движение: выведенная из положения равновесия, она возвращается в это поло­жение, не совершая колебаний.