23.6. Альтернативный оптимум в транспортных задачах

Признаком наличия альтернативного оптимума в транспо­ртной задаче является равенство нулю хотя бы одной из оце­нок свободных переменных в оптимальном решении (X_опт1).Сделав перераспределение грузов относительно клетки, име­ющей Δ_ij = 0, получим новое оптимальное решение (Х_опт2), при этом значение целевой функции (транспортных расходов) не изменится. Если одна оценка свободных переменных равна нулю, то оптимальное решение находится в виде

где 0 ≤ t ≤ 1.

Рассмотрим конкретную задачу, имеющую альтернатив­ный оптимум.

Пример 1. На трех складах имеется мука в количестве 60, 130 и 90 т, которая должна быть в течение месяца доставлена четырем хлебозаводам в количестве: 30, 80, 60, 110 т соответ­ственно. Составить оптимальный план перевозок, имеющий минимальные транспортные расходы, если стоимость доставки 1 т муки на хлебозаводы задана матрицей

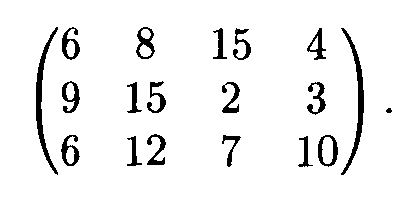
Решение. Составим распределительную таблицу в виде табл. 23.6.

По методу минимального тарифа найдем исходное реше­ние. Определим потенциалы строк и столбцов. Найдем оценки свободных клеток:

Так как Δ₁₂ = 4 > 0, то перераспределим грузы относи­тельно клетки (1,2):

Занесем полученное перераспределение грузов в распреде­лительную таблицу и вычислим потенциалы занятых и оценки свободных клеток (табл. 23.7).

Получим

Так как Δ₃₃ = 0, то задача имеет альтернативный оптимум и одно из решений равно

Стоимость транспортных расходов составляет: L(X_опт1) = 1550 усл. ед.

Произведем перераспределение грузов относительно клетки (3,3):

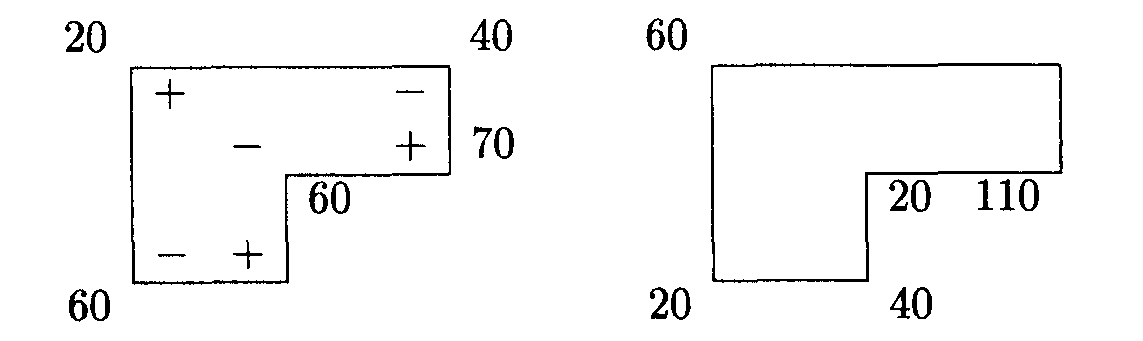
Занесем в распределительную таблицу полученное пере­распределение грузов, вычислим потенциалы занятых и оценки свободных клеток (табл. 23.8):

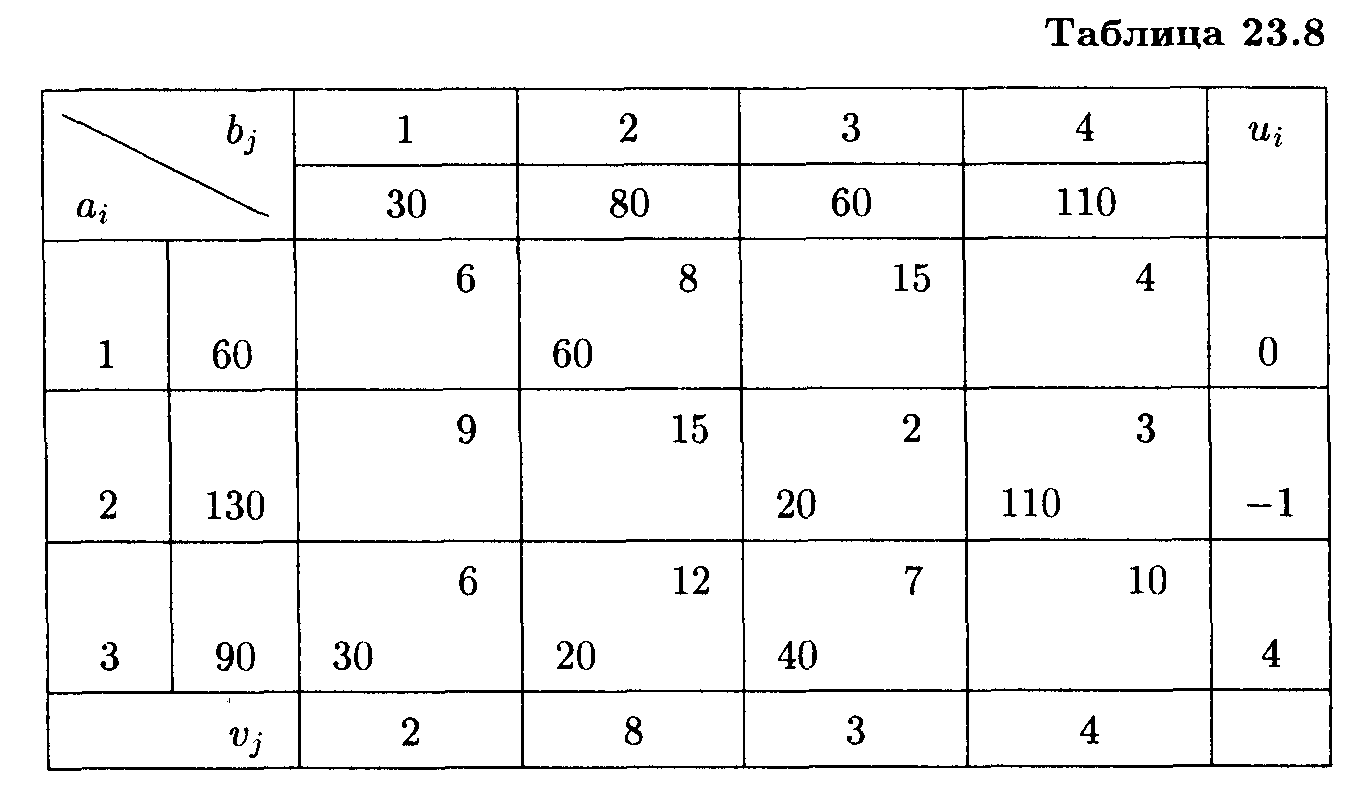
Так как Δ₁₄ = 0, получили еще одно решение:

Стоимость транспортных расходов составит L(Х_опт2) = 1550 усл. ед.

Данная задача имеет два оптимальных решения Х_опт1 и X_опт2, общее решение находится по формуле

где 0 ≤ t ≤ 1.

Найдем элементы матрицы общего решения:

Итак,

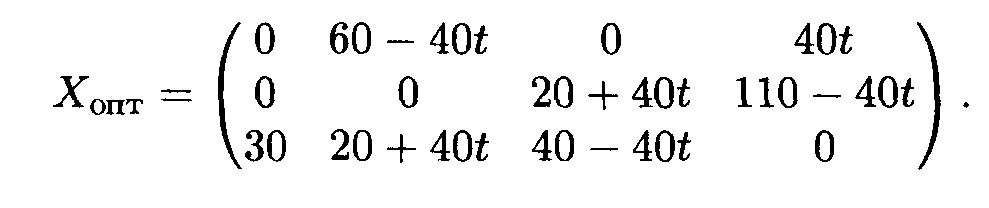
Стоимость транспортных расходов составляет 1550 усл. ед.

23.7. Вырожденность в транспортных задачах

При решении транспортной задачи может оказаться, что число занятых клеток меньше, чем m + п - 1. В этом слу­чае задача имеет вырожденное решение. Для возможного его исключения целесообразно поменять местами поставщиков и потребителей или ввести в свободную клетку с наименьшим тарифом нулевую поставку. Нуль помещают в такую клетку, чтобы в каждой строке и каждом столбце было не менее одной занятой клетки.

Рассмотрим вырожденность в транспортной задаче на при­мере.

Пример 2. Фирма осуществляет поставку бутылок на три за­вода, занимающиеся производством прохладительных напит­ков. Она имеет три склада, причем на складе 1 находится 6000 бутылок, на складе 2 — 3 000 бутылок и на складе 3 — 4 000 бутылок. Первому заводу требуется 4000 бутылок, второму за­воду — 5 000 бутылок, третьему заводу — 1000 бутылок. Мат­рицей

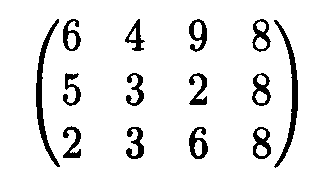
задана стоимость перевозки одной бутылки от каждого склада к каждому заводу.

Как следует организовать доставку бутылок на заводы, чтобы стоимость перевозки была минимальной?

Решение. Запишем исходные данные в распределитель­ную таблицу (табл. 23.9), найдем исходное опорное решение по методу минимального тарифа. Число заполненных клеток равно 5, т + п - 1 = 6, следовательно, задача является вырож­денной.

Для исключения вырожденности необходимо в какую-то клетку ввести нулевую поставку. Такая клетка становится условно занятой, ее целесообразно определить при вычислении потенциалов занятых клеток, она должна иметь наименьший тариф по сравнению с другими клетками, которые могут быть условно занятыми.

Так, для нахождения потенциала и₃ поместим нулевую по­ставку в клетку (3,2), после чего представляется возможным вычислить остальные потенциалы.

Оценки свободных клеток следующие:

Все оценки отрицательные, получили оптимальное реше­ние:

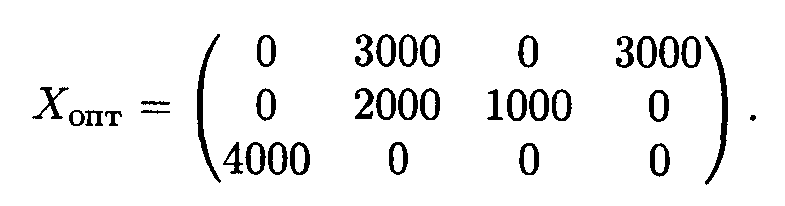
Таким образом, со склада 1 целесообразно поставить 3000 бутылок второму и четвертому заводам, со склада 2 — 2000 бутылок второму заводу и 1000 бутылок третьему, со склада 3 — 4000 бутылок первому заводу, при этом стои­мость транспортных расходов будет минимальной и составит 28 000 усл. ед.