§ 3. Соединения балок со стойнами

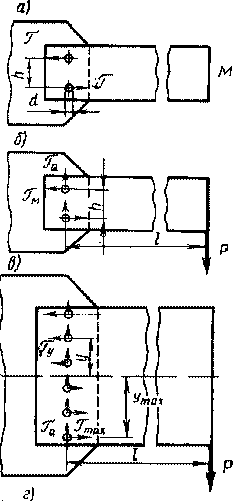
На рис. 17-4 приведено сварное соединение балки со стойкой. Оно выполнено обварнванием по периметру поперечного сечения

балки и установкой уголка и является типовым.

420

На рис. 17-5 приведен пример сопряжения балки двутаврово­го профиля со стойкой с помощью коротких вертикальных швов. Между полками балки и стойкой оставлены небольшие зазоры Д = Ь:-2 мм, которые обеспечивают шарнирность соединения. При этом волокна, наиболее удаленные от нейтральной оси, мо­гут свободно деформироваться. Расчет прочности такого вида сопряжений производят на поперечную силу. Эти соединения применяют в США. У нас их используют редко ввиду недоста­точно надежного характера работы.

§ 4. Точечные соединения рам, работающих на изгиб

Пример точечного соединении, работающего на изгиб, приве­ден на рис. 17-6, а. Изгибающий момент уравновешивается парой сил Т, возникающих в точках.

Усилие в каждой точке

Напряжение в точке

=	М h
т		Ш
F	~	йта/а

Т = ^-. (17.3)

(17-4)

где h — расстояние между центрами точек; d — диаметр точки. Пример точечного соединения, работающего на поперечный изгиб, приведен на рис. 17-6,6. В соединениях возникают;

изгибающий момент поперечная сила усилие от момента

М = РЦ (17.5)

Q^P; (17.6)

т —1L ¹ м~ н

Напряжение в точке от изгибающего момента

— ^{4М z}m — _ктф •

Усилие в точке T_Q от поперечной силы Q, равной Р, опреде­ляется в предположении равномерного распределения усилий между точками, входящими в соединения,

т - ^Q t _Q— ₂ .

421

Напряжение в точке от Q

"'Q

2Q

т.а*

где тдг направлено горизонтально, x_Q — вертикально.

Результирующее напряжение в точке определяется по фор­муле

V» *= К-й + *Ь < И'1. (17.7)

Более сложная конструкция точечного соединения приведена на рис. 17-6,6. Принимаем, что распределение напряжений в се­чении от изгибающего момента происходит по линейному закону. При этом распределение усилий между точками неравномерное; наиболее напряженными в соеди­нении оказываются крайние точки.

В силу линейного закона рас­пределения напряжений

-у - ~-i У. где х_у — напряжение в точке, на­ходящейся на расстоя­нии у от нейтральной оси элемента; Ti — напряжение на расстоя­нии, равном единице от нейтральной оси. Момент внутренних сил, воз-МШ пикающих в точках, уравновеши-

вает внешний момент

^^ЖИ1

т --- т„

— у-

(17.8)

Полная величина изгибающе­го момента равна

Ж = £т, ^' у. (17.9)

Заменяя т его значением X\ij, находим изгибающий момент

Рис. 17-6. Точечные соединения, работающие на М н Q

м

ltd*

*У\

(17.10)

422

откуда

ъ=-1ащг- ^(17Л1)

Напряжение в точке, наиболее удаленной от нейтральной оси, определяется по формуле

^max rd'^tv² Ушах* \ii.lZ)

Напряжение, вызванное поперечной силой, равно

где п — количество односрезных точек в вертикальном ряду.

При наличии / вертикальных рядов точек напряжение от изгиба будет

4М /-,-7 ,л

У max, (17.14)

а напряжение от Q

=«=1^г- (17.15)

Результирующее напряжение должно быть

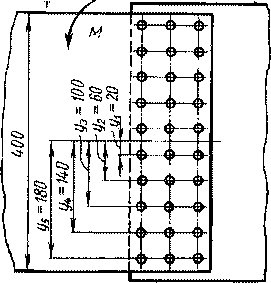
Пример расчета. Требуется сконструировать крепление листа сечением 400X4 мм, равнопрочное по изгибу основному элементу (рис. 17-6,г). Нагрузка статическая.

Изгибающий момент, воспринимаемый основным листом, равен

= 106,6 [oj_p кГ -см, Диаметр сварной точки принимаем равным d *=■ 1,5 s + 5 — 11 мм.

Расстояние между односрезными точками при толщине листа 4 мм принимаем 4 см. Расстояние точек до оси у_}=2 см, #2 — 6 см; #з = 10 см; #4=14 см; //₅~18 см.

Число рядов точек (рис. 17-6,г), равное 3, обозначим че­рез /.

423

Из формулы (17.14) находим /, заменяя т_гаах через [х% где К| = 0,5[о]_р;

Еу2^(2³ + б²|-10--|- 14²+ 18'^J) -2- 1320 см², Определим число рядов

4 ■ 106,6 Ы₀ ■ 18

~ 3,14 - 1,1» ■ 1320 ■ 0,5 [о]_р ~ ^z,JO-

Принимаем три вертикальных ряда точек.