Вчитель математики: Ковальова Світлана ІванІвна
Відповіді на письмові завдання принести до школи до 15.09.2014 або відіслати за адресою:
sveta611.kov@yandex.ru
Телефон для довідок - 0958472358
Повторення за 6 клас.
1) Дільник і кратне
Дільником натурального числа називається число, на яке ділиться дане число без остачі:
42 1, 2, 3, 6, 7, 14, 21, 42 (8 дільників)
Кратним даному натуральному числу називається число, яке ділиться на дане без остачі:
на 8 – 8, 16, 24… (безліч кратних)
2) Ознаки подільності
на 2 : остання цифра парна
на 5 : остання цифра 0 або 5
на 10 : остання цифра 0
на 3 : сума цифр ділиться на 3
на 9 : сума цифр ділиться на 9
3) Прості і складені числа
Будь-яке число, що має тільки 2 дільники, називається простим (2, 3, 5, 7, 11…). Число, яке має більше двох дільників, – складеним (4, 6, 8, 9, 10…).
4) Розкладання на прості множники
630
2 630=
5
63 3
21 3
7 7
1
5) Найбільшим спільним дільником двох чисел називається найбільше число, на яке діляться дані числа:
72
2~ 80 2
2~ 2
2 3 НСД (72, 180) = 22 ∙ 32 = 36
3~ 3
3~ 5
6) Найменшим спільним кратним двох чисел називається найменше число, яке ділиться на обидва дані числа:
НСК (72, 180) = 180 · 2 = 360
Для декількох чисел НСК дорівнює добутку всіх множників у найбільшому степені:
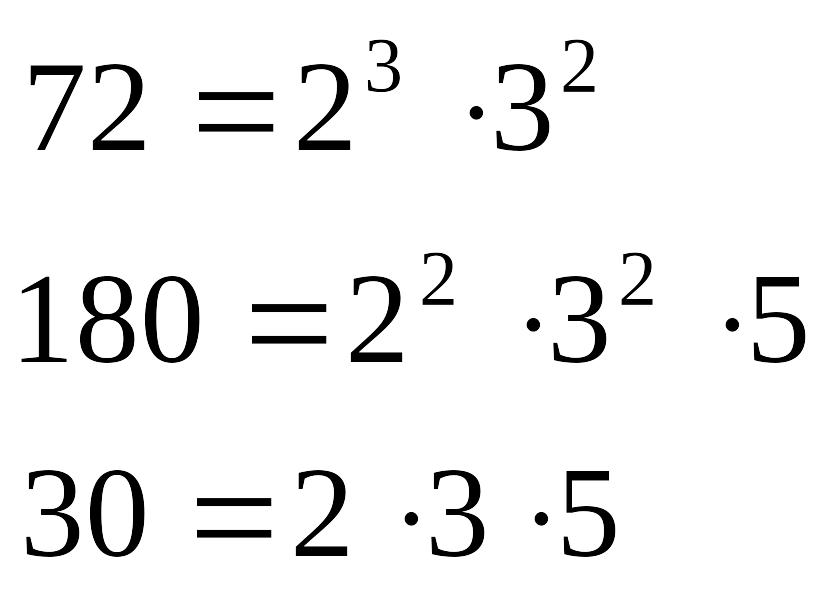НСК
(72, 180, 30) = 23
· 32
· 5 = 360
7) Основна властивість дробу
Якщо чисельник і знаменник дробу помножити або поділити на одне й те саме натуральне число, то дістанемо дріб, що дорівнює даному:
8) Скоротити дріб означає поділити чисельник і знаменник на їхній спільний дільник:
9) Порівняння звичайних дробів
1) З двох дробів з однаковими знаменниками більше той, у якого чисельник більший:
>
2) З двох дробів з однаковими чисельниками більше той, у якого знаменник менший:
>
3) Щоб порівняти дроби з різними чисельниками і знаменниками, треба звести їх до спільного знаменника:
10) Додавання (віднімання) дробів
Відповідь скоротити (якщо можливо) і виділити цілу частину (якщо дріб неправильний).
11) Множення дробів
При множенні мішаних дробів їх перетворюють у неправильні дроби:
12) Ділення дробів
Щоб поділити один дріб на другий, треба перший дріб помножити на дріб, обернений до другого:
13) Масштаб – це відношення двох чисел, яке показує, у скільки разів відстань на малюнку менша за відстань на місцевості:
М 1:1 000 000
1см – 10 км
14) Пропорції
Рівність двох відношень називають пропорцією:
10 : 5 = 2 : 1
середні
крайні
15) Основна властивість пропорції
Добуток крайніх членів пропорції дорівнює добутку її середніх членів:
10
· 1,5 = 3 · 5
16) Щоб знайти невідомий середній член пропорції, треба помножити крайні члени і поділити на відомий середній:
48 : х = 12 : 5
х = 48 · 5 : 12
17) Щоб знайти невідомий крайній член пропорції, треба помножити середні члени і поділити на відомий крайній:
х : 52 = 5 : 13
х = 52 · 5 : 13
18) Дві величини називаються прямо пропорційними, якщо при збільшенні однієї з них інша збільшується в стільки ж разів:
I a x b : a = c : х
II ↑ b c ↑
19) Дві величини називаються обернено пропорційни- ми, якщо при збільшенні однієї з них інша зменшується в стільки ж разів:
I а км/год х год b : а = х : с
II ↑ b км/год c год ↓