III. Первые сведения о треугольниках. Параллелограммы § 15. Сумма углов треугольника Предварительные упражнения
Предварительные упражнения
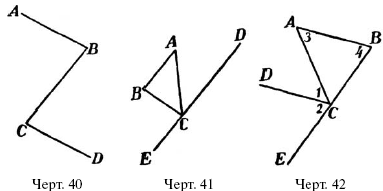
1) На черт. 40 линии АВ и CD параллельны. Укажите в фигуре ABCD равные углы.
2) На черт. 41 DЕ параллельно АВ. Укажите равные углы в этой фигуре.
3) На черт. 42 CD параллельно АВ. Укажите равные углы в этой фигуре.
4) Докажите, что на черт. 42 уг. 1 + уг. 2 = уг. 3 + уг. 4.
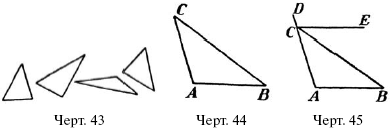
Познакомившись со свойствами отдельных прямых линий и углов, перейдем к изучению з а м к н у т ы х фигур. Начнем с фигуры, называемой т р е у г о л ь н и к о м. Это – фигура, ограниченная тремя прямыми линиями; у нее три угла, вершины которых называются вершинами треугольника. Треугольники могут иметь весьма разнообразную форму, в зависимости от величины углов (черт. 43).
Главное свойство всякого треугольника состоит в том, что какова бы ни была длина его сторон и какую бы форму он ни имел, сумма его трех углов всегда одинакова: она равна двум прямым углам. Покажем, как в этом убедиться.
Рассмотрим для примера треугольник ABC(черт. 44). Продолжим сторону АС за вершину С, как показано на черт. 45
Получим угол BCD’, такие углы называются в н е ш‑н и м и углами треугольника (в отличие от в н у т р е н‑н и х). Легко убедиться, что этот угол должен равняться сумме несмежных с ним внутренних углов А и В. Для этого достаточно лишь провести через вершину С прямую СЕ, параллельную противолежащей стороне АВ. Тогда из двух углов, на которые разделится внешний угол DCВ, один – угол DCE– равен углу А, потому что это соответственные углы при параллельных СЕ и АВ; а другой угол ЕСВ равен углу В, потому что это перекрестные углы при тех же параллельных. Отсюда уг. А + уг. В = углу DCВ. Следовательно, уг. А + уг. В + уг. АСВ = уг. DCB+ ACB = двум прямым углам.
Приведенное рассуждение мы можем приложить ко всякому треугольнику, какой бы формы и величины он ни был. Во всех случаях мы убедимся, что
С у м м а у г л о в т р е у г о л ь н и к р а в н а д в у м п р я м ы м у г л а м, т. е. 180°.
Повторительные вопросы
Какая фигура называется треугольником? – Сколько у треугольника вершин? Покажите их на чертеже. – Покажите на чертеже внешний угол. – Какая зависимость существует между внешним углом и несмежными с ним внутренними? Как в этом убедиться? – Чему равна сумма углов всякого треугольника?
§ 16. Следствия предыдущего параграфа
Предварительные упражнения
1) Попробуйте начертить треугольник с двумя тупыми углами. С одним тупым и одним прямым. С двумя прямыми.
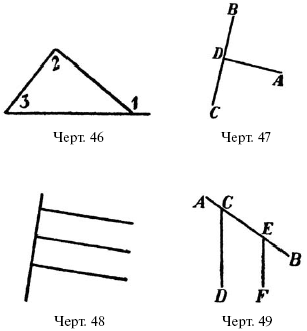
2) Какой из углов на черт. 46 больше: уг. 1 или уг. 3? Уг. 1 или у г. 2?
3) Из точки D (черт. 47) проведен к прямой ВС перпендикуляр DА. Можно ли через ту же точку Dпровести к ВС еще один перпендикуляр, который не сливался бы с DA?
4) К прямой АВ (черт. 48) проведены три перпендикуляра. Пересекутся ли они между собой, если продолжить их в обе стороны?
5) Прямую АВ (черт. 49) встречают две прямые CDи EFпод равными со ответственными углами. Пересекутся ли эти две прямые, если продолжить их в обе стороны?
Из свойств суммы углов треугольника вытекает ряд других свойств фигур. Заметим некоторые из них:
1) В т р е у г о л ь н и к е н е м о ж е т б ы т ь б о л ь ш е о д н о г о т у п о г о у г л а (подумайте, какова должна была бы быть сумма всех углов треугольника, если бы три или два его угла были тупые, т. е. больше прямого).
2) В т р е у г о л ь н и к е н е м о ж е т б ы т ь б о л ь ш е о д н о г о п р я м о г о у г л а (почему?)
3) В н е ш н и й у г о л т р е у г о л ь н и к б о л ь ш е к а ж д о г о н е с м е ж н о г о с н и м в н у т р е н н е г о (см. черт. 45).
Черт. 48 Черт. 49
4) Ч е р е з т о ч к у, л е ж а щ у ю в н е п р я м о й, м о ж н о п р о в е с т и к э т о й п р я м о й т о л ь к о о д и н
п е р п е н д и к у л я р. – Если бы, например (черт. 50), к прямой МN можно было провести из точки А больше одного перпендикуляра, – скажем, кроме АВ еще АС, – то в треугольнике ABCоказалось бы два прямых угла, а это, мы знаем, невозможно.
5) Н е с к о л ь к о п е р п е н д и к у л я р о в к о д н о й п р я м о й л и н и и (черт. 48) в с е г д а п ар а л л е л ь н ы
м е ж д у с о б о ю. Если бы они были не параллельны, т. е. если бы они встречались, то составились бы треугольники с двумя прямыми углами каждый.
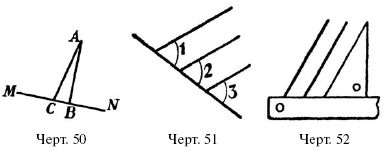
6) П р я м ы е л и н и и, в с т р е ч а ю щ и е о д н у и т у ж е п р я м у ю п о д р а в н ы м и с о о т в е т с т в е н н ы м и
у г л а м и (черт. 51), п а р а л л е л ь н ы м е ж д у с о б о й. – Если бы они были не параллельны, т. е. если бы встречались, то уг. 2, например, оказался бы внешним углом треугольника, а р а в н ы й е м у уг. 1 – внутренним углом того же треугольника; но это невозможно (см. следствие 3‑е).
На последнем свойстве основан способ проводить параллельные линии с помощью линейки и чертежного треугольника (черт. 52).
Повторительные вопросы
Могут ли три угла треугольника быть тупыми? А только два угла? – Может ли в треугольнике быть три прямых угла? А два прямых угла? (Попробуйте начертить такой треугольник). – Сколько перпендикуляров можно провести к прямой линии из внешней точки? – Каким свойством обладают два перпендикуляра к одной прямой? – Каким свойством обладают две прямые, встречающие третью под равными соответственными углами? – Как чертят параллельные помощью линейки и чертежного треугольника?