II. Углы. Первые сведения об окружности. Параллельные прямые1 § 4. Углы и их обозначения

Когда прямые линии встречаются, они образуют в местах встречи «углы». Угол – две прямые, исходящие из одной точки. Прямые эти называются с т о р о н а м и угла, а точка, в которой они сходятся, – вершиной угла.

Для обозначения углов употребляют три буквы: две ставятся у сторон, третья – у вершины. Называя угол, начинают с буквы, стоящей у одной стороны, затем называют букву у вершины и, наконец, – букву возле другой стороны. В том же порядке и записывают углы. Например, верхний угол фигуры черт. 12 есть ABC(или СВА); левый угол той же фигуры – ВАС, правый – АСВ (последние два угла можно также назвать CAB и ВСА).

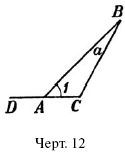
Употребляются и иные способы обозначения углов. Можно, например, называть одну только букву, стоящую у вершины: верхний угол фигуры черт. 12 можно по этому способу назвать: у г. В. Но угол ВАС нельзя назвать «уг. А», так как у точки А лежат вершины двух углов: ВАС и BAD.

Нередко обозначают угол м а л о й буквой или цифрой, ставя их в н у т р и угла, близ вершины. Например, уг. ABCможно обозначить как «уг. а», уг. ВАС – как «уг. 1». Между сторонами угла проводят иногда для ясности дужку (см. уг. 1 черт. 12).

Повторительные вопросы

Какая фигура называется углом? – Покажите на чертеже, где вершина угла, и где его стороны? – Какие вы знаете способы обозначения углов?

§ 5. Сравнение углов. Сложение и вычитание углов

Углы различают по их величине. Большим считается не тот угол, стороны которого длиннее, а тот, стороны которого сильнее расходятся врозь. На черт. 13 уг. EDF больше, чем угол 2, потому, что у первого стороны сильней расходятся врозь. Встречаются углы, стороны которых расходятся врозь совершенно одинаково; такие углы можно наложить один на другой так, что их вершины совпадут, а стороны сольются. Углы, которые можно таким образом наложить друг на друга, считаются равными, хотя бы стороны их были неодинаковой длины.

На черт. 13 равны, например, уг. DEH и уг. DFH, уг. 2 и уг. а; вы можете убедиться в этом, есля обведете один угол на прозрачной бумаге и покроете им другой.

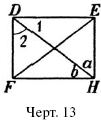
Если при наложении сравниваемых углов их вершины и одна сторона совпали, вторая же сторона накладываемого угла оказалась внутри или вне другого угла, то такие углы, конечно, не равны. Тот угол, который оказался внутри другого, считается меньшим.

Рассмотрите на том же черт. 13 углы, вершины которых лежат в точке D. Здесь три угла: уг. EDF, уг. EDHи уг. HDF. Вы видите, что оба меньших угла как раз заполняют собою уг. EDF, который составляется из них, как целое из своих частей. Когда углы так расположены, то говорят, что уг. EDFесть с у м м а углов EDHи HDF. С л о ж и т ь два угла значит найти их сумму, т. е. тот угол, который составится, если приложить их друг к другу, как показано на чертеже 13.

Если на черт. 13 от угла EDFотнять угол EDH, то останется уг. HDF; этот. угол называется р а з н о с т ь ю углов EDFи EDH. Вычесть один угол из другого значит найти их разность.

Повторительные вопросы

Какие углы называются равными? – Зависит ли величина угла от длины сторон? – Покажите на чертеже, что называется суммой и разностью двух углов.