Глава 3 Синтаксис языка ассемблера
Язык ассемблера, называемый также языком символического кодирования, представляет собой машинный язык в символической форме, которая более понятна и удобна программисту. Сложная внутренняя структура, разнообразные форматы команд, многочисленные режимы адресации процессоров Intel ограничивают возможности разработки сложных и объемных программ на языке ассемблера. Однако в любых сложных программах всегда существуют критические секции, требующие интенсивных и быстрых вычислений, которые приходится разрабатывать не на языке высокого уровня, а на ассемблере.
Разработка программ на языке ассемблера требует хороших знаний архитектуры всей системы, включая режимы адресации данных, структуры памяти и системы команд процессора. Поэтому анализ возможностей ассемблера мы будем проводить в тесной взаимосвязи с архитектурой процессоров Intel Pentium. Напомню, что мы рассматриваем язык ассемблера, основанный на разработке фирмы Microsoft версии 6.14 и выше. Он включает в себя множество параметров, команд и директив, анализ которых займет много времени. Поэтому здесь будут рассмотрены только наиболее важные языковые конструкции, без знания которых создавать программы невозможно. Для такого анализа нужно четко понимать, как данные представляются в компьютере и каковы общие принципы их обработки, поэтому начнем именно с этого.
3.1. Представление данных в компьютере
В основе работы компьютера лежат понятия бита и байта – именно они представляют данные и команды в памяти. Минимальной единицей информации в компьютере является бит. Бит может принимать одно из двух значений: 0 или 1 – и является составным элементом для более информативных единиц данных. Минимальный объем информации, к которому имеется доступ в памяти компьютера, составляет один байт (8 двоичных разрядов, или битов), при этом говорят о байтовой организации памяти (хотя теоретически память может быть организована и по‑другому). Все байты оперативной памяти нумеруются начиная с нуля. Местоположение каждого байта в памяти характеризуется его номером или, по‑другому, адресом. Схематически байт представляет собой структуру данных, изображенную на рис. 3.1.
Рис. 3.1. Представление байта
Старший бит байта имеет номер 7, младший – 0. В оперативной памяти машины байты данных располагаются по возрастанию адресов (рис. 3.2).
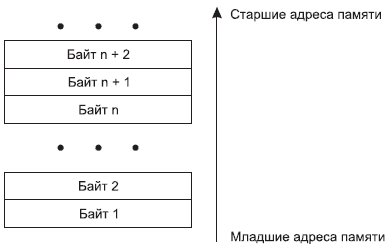
Рис. 3.2. Адресация памяти
Исключение составляет специальная область памяти, называемая стеком, – в ней байты данных располагаются в сторону убывания адресов. Более подробно мы рассмотрим стек в последующих главах.
Редко случается так, что для представления данных требуется один байт. Во многих случаях данные нужно представить большим числом байтов. Если данные можно представить двумя байтами, то говорят, что они представлены словом. О данных, требующих для представления 4 байта, говорят, что они имеют размерность двойного слова. Наконец, данные могут быть представлены восемью (учетверенное слово) или шестнадцатью (двойное учетверенное слово) байтами. Во всех этих случаях расположение байтов соответствует правилу: младший байт располагается по младшему адресу, а старший байт – по старшему (рис. 3.3).
Нумерация байтов в обычных, двойных и учетверенных словах начинается с младшего (нулевого) байта и заканчивается 1, 3 и 7‑м байтом соответственно. В документации часто используется такой способ расположения байтов, когда старшие байты располагаются слева, а младшие – справа. Пример такого расположения байтов в двойном слове показан на рис. 3.4.
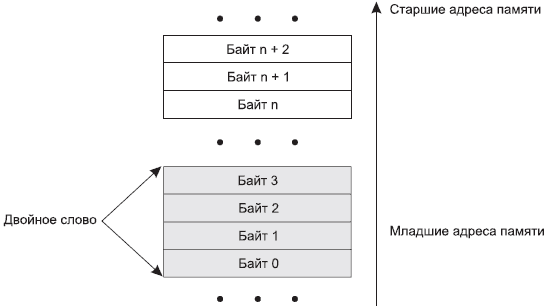
Рис. 3.3. Представление данных различной размерности в памяти
Крайний слева байт принято называть старшим, а крайний справа – младшим. Такой порядок расположения байтов связан с обычной для нас формой записи чисел, когда в многоразрядном числе слева находятся старшие разряды, а справа – младшие. Следующее число опять начнется со старшего разряда и закончится младшим. Однако в памяти компьютера данные располагаются в более естественном порядке непрерывного возрастания номеров байтов, и, таким образом, каждое слово или двойное слово в памяти начинается с младшего байта и заканчивается старшим (см. рис. 3.4).
Рис. 3.4. Расположение байтов двойного слова
Вкратце напомню, как интерпретируются числовые данные в компьютере. Комбинируя двоичные цифры (биты), можно представить любое числовое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Рассмотрим восьмибитовое число (байт), представленное следующим образом:
10100101
Поскольку мы имеем дело с двоичной системой счисления, то это число можно представить так:
Значение этого числа в десятичной системе равно 165. Таким образом, любое двоичное число, имеющее и разрядов, можно представить в виде
Здесь k может принимать одно из двух значений: 0 или 1. Разрядность и двоичного числа определяется архитектурой системы и обычно кратна восьми. Сразу замечу, что мы рассматриваем двоичное представление целых чисел, являющееся базисом для понимания вычислительных операций с любыми другими типами чисел, такими, например, как вещественные числа или, в терминологии ассемблера, «числа с плавающей точкой».
В арифметических операциях задействованы положительные и отрицательные целые и вещественные числа, поэтому необходимо каким‑то образом различать их знаки. Знак двоичного числа указывается старшим или, как его называют, знаковым битом числа. Положительные числа имеют в старшем разряде нулевой бит, а отрицательные числа – единичный. Отрицательные двоичные числа выражаются двоичным дополнением, то есть для представления отрицательного двоичного числа необходимо инвертировать все его биты и к результату прибавить 1.
В следующем примере находится двоичное представление числа ‑61. Положительное число 61 представляется как 00111101, а процесс преобразования показан далее:
Несколько слов об операции сложения. Она выполняется по простым правилам:
0 + 0 = 0 1+0=1
0 + 1 = 1
1 + 1 = 0 + 1 (бит переноса)
Как и в десятичной системе счисления, при выходе за пределы разрядной сетки для данного разряда образуется единица переноса в следующий разряд. Это продемонстрировано на рис. 3.5.
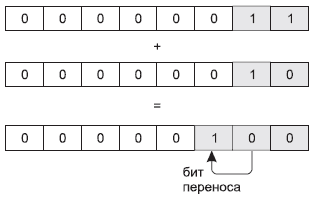
Рис. 3.5. Схема сложения двоичных чисел с переносом
Проверить результат преобразования положительного числа в отрицательное очень просто: достаточно сложить оба числа, при этом результат должен быть нулевым. Например, если сложить числа 61 и ‑61, должен получиться 0:
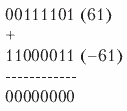
Результат получился нулевым, что свидетельствует о корректности преобразования. Перенос из самого старшего разряда при этом теряется.
Вычитание двоичных чисел выполняется как модифицированный вариант сложения, при этом вначале инвертируется знак вычитаемого, после чего числа складываются. Это обусловлено тем, что операционный блок процессора содержит только устройства сложения (сумматоры) и не имеет устройств вычитания.
Приведу простой пример. Пусть требуется из числа 5 вычесть 2. Эту операцию можно представить как 5 + (‑2). Число 5 представляется в двоичной форме как 00000101, а число ‑2 – как 11111110. Результат вычисляется следующим образом:
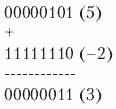
Здесь я хочу сделать важное замечание. Процессор ничего не «знает» о знаковых и беззнаковых числах, он просто складывает биты операндов, поэтому вся ответственность за интерпретацию результатов ложится на прикладные программы. Операции умножения и деления алгоритмически более сложны, но в их основе также лежат операции сложения и вычитания.
Представление двоичных чисел в виде последовательности нулей и единиц часто бывает не очень удобным из‑за своей громоздкости и не очень хорошей читабельности. Во многих случаях используется так называемое шестнадцатеричное представление чисел. Такая система счисления включает символы от 0 до F и, поскольку таких символов 16, называется шестнадцатеричной. Шестнадцатеричный формат нашел широкое применение в языке ассемблера. В ассемблерных листингах программ в шестнадцатеричном формате показаны все адреса, машинные коды команд и содержимое констант. Отладочная информация также выдается в шестнадцатеричном формате.
В табл. 3.1 приведены десятичные, двоичные и шестнадцатеричные значения чисел от 0 до 15.
Если немного поработать с шестнадцатеричным форматом, то можно быстро к нему привыкнуть.
Таблица 3.1. Соответствие между десятичными, двоичными и шестнадцатеричными числами
Для того чтобы различать форматы чисел, в языке ассемблера приняты специальные обозначения: В, b – двоичные числа; H, h – шестнадцатеричные числа. Приведу несколько примеров чисел в разных форматах:
56 = 00111000b = 38h
‑13= 11110101 = F5h
Сложение и вычитание чисел в шестнадцатеричном формате осуществляется по тем же правилам, что и двоичных или десятичных чисел: операция выполняется для каждого разряда с учетом переноса из младшего разряда или заема из старшего. Рассмотрим несколько примеров.
Пусть требуется сложить два числа в шестнадцатеричном формате: 3Fh и 27h:
При сложении младших разрядов, равных F и 7, результирующее значение равно 22 (в десятичной системе), то есть младший разряд будет равен 22 – 16 = 6, при этом происходит перенос в старший разряд. При сложении старших разрядов результирующее значение вычисляется как 3 + 2 + бит переноса, то есть окончательный результат равен 66L
В следующем примере необходимо вычесть шестнадцатеричное значение 7Eh из AAh:
При вычитании младших разрядов, равных А (10 в десятичной системе) и Е (14 в десятичной системе), необходим заем из старших разрядов. Тогда значение младшего разряда будет равно 16 + 10 – 14 = 12 или в шестнадцатеричной форме – С. Результат вычитания старших разрядов будет равен 9‑7 = 2. Окончательный результат вычитания равен 2CL
Двоичные числа используются не только в вычислениях, но и для другой функции – с их помощью можно выводить информацию в символьном представлении на экран дисплея или периферийное устройство печати. Для стандартного представления таких символов используется код ASCII (American National Standard Code for Information Interchange – Американский национальный стандартный код для обмена информацией).
Представление символа А в соответствии со стандартом ASCII выражается шестнадцатеричным значением 41h, представление символа В – значением 42h и т. д. Наличие стандартного кода облегчает обмен данными между различными устройствами компьютера. При этом 8‑битовый расширенный код ASCII, используемый в компьютерах, обеспечивает представление 256 символов, включая символы национальных алфавитов.