8

5 Постоянный электрический ток

5.1 Сила и плотность тока

Электрическим током называется направленное движение электрического заряда. Ток может протекать в металлах, полупроводниках, жидкостях (электролитах) и газах (газовый разряд).

Для протекания тока необходимы два условия: наличие свободных носителей заряда и наличие электрического поля.

При включении электрического поля на хаотическое (тепловое) движение носителей накладывается упорядоченное движение с некоторой средней скоростью и через воображаемую поверхность S проходит ток.

Количественной характеристикой тока является заряд, проходящий через рассматриваемую поверхность за единицу времени,

За направление тока принимают направление движения положительных зарядов.

Электрический ток может неравномерно протекать через поверхность. Для более детального, локального описания тока вводят вектор плотности тока , модуль которого численно равен отношению силы тока через элементарную площадку, расположенную в данной точке перпендикулярно направлению движения носителей, к ее площади:

.

Поле вектора можно, также как и для вектора , изображать в виде линий тока или линий вектора .

Если носителями тока являются заряды разных знаков, то плотность тока: . Оба слагаемые имеют одинаковое направление. Поскольку, , то , здесь плотность тока выражена через объемные плотности положительных и отрицательных зарядов.

Зная в каждой точке поверхности S, можно найти и силу тока через всю поверхность как поток вектора через эту поверхность:

Из формулы видно, что сила тока величина скалярная и алгебраическая, знак определяется, кроме всего прочего, выбором нормали к S.

5.2 Уравнение непрерывности

Рис.5.1

Выделим в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Нормаль к ней, как известно, берут снаружи, рис.5.1, значит вектор тоже направлен наружу. Проанализируем физический смысл интеграла . Здесь - элементарный ток через площадку ,перпендикулярную вектору тогда - сумма всех элементарных токов, ток или заряд в единицу времени, вышедший наружу через всю поверхность S из объема, охватываемого этой поверхностью. В соответствии с законом сохранения электрического заряда, этот интеграл равен убыли заряда в единицу времени внутри объема V проводника, т.е.,

. Это выражение называется уравнением непрерывности, по существу это закон сохранения заряда.

Левую часть уравнения можно преобразовать по теореме Остроградского –Гаусса:

, а правую - записать через объемную плотность заряда:

. Частная производная, т.к. зависит не только от времени, но и от координат, в отличие от . Приравнивая левую и правую части, получим:

. Равенство выполняется для произвольного объема, по которому берется интеграл, это значит, что оно выполняется для каждой точки пространства:

- уравнение непрерывности в дифференциальной форме.

Там, где  0, т.е., в точках, которые являются источниками вектора , происходит убывание заряда и наоборот.

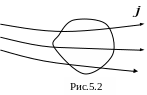
Для стационарного случая, т.е. для постоянного тока, плотность заряда, потенциалы и другие величины в данной точке остаются неизменными. Следовательно, и или . Это значит, линии вектора нигде не начинаются и не заканчиваются, т.е. в этом случае поле вектора не имеет источников в этом объеме. Число линий, входящих в объем V равно числу линий, вышедших из него, рис.5.2.