2.10 Связь между и на границе раздела проводник-диэлектрик.

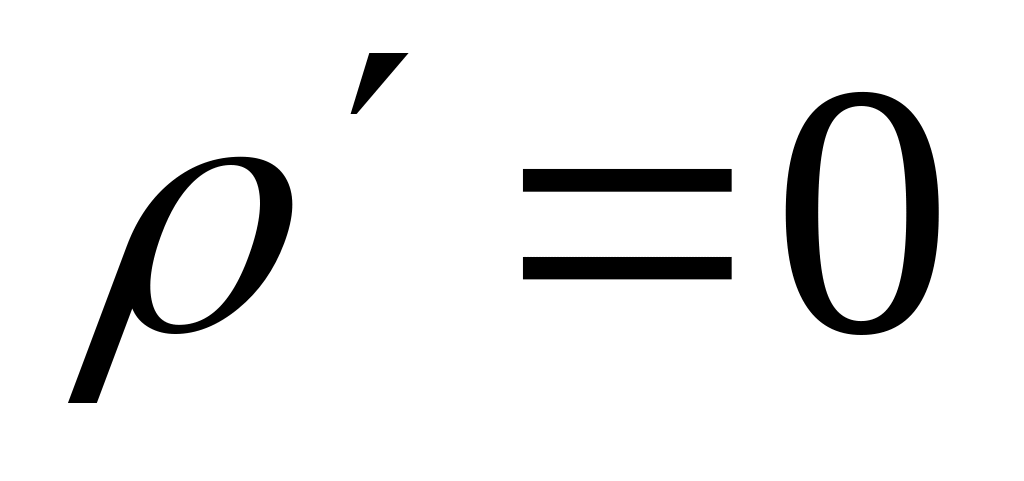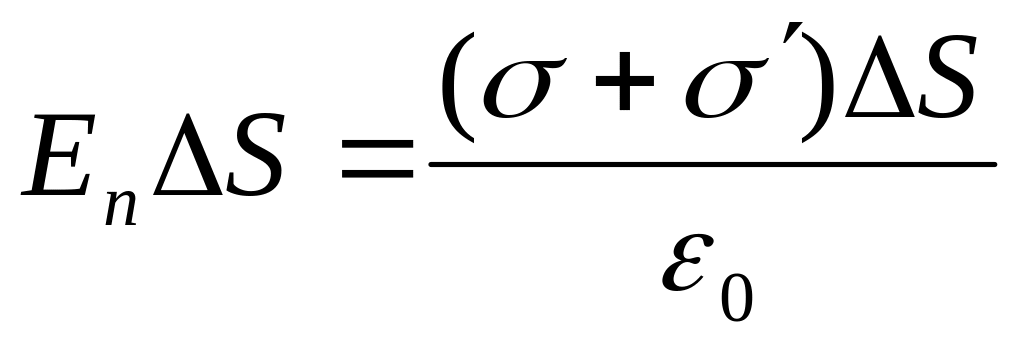Для границы раздела проводника (среда 2) и однородного ( ) диэлектрика (среда 1), рис.2.9, запишем теорему Гаусса: , с другой стороны, 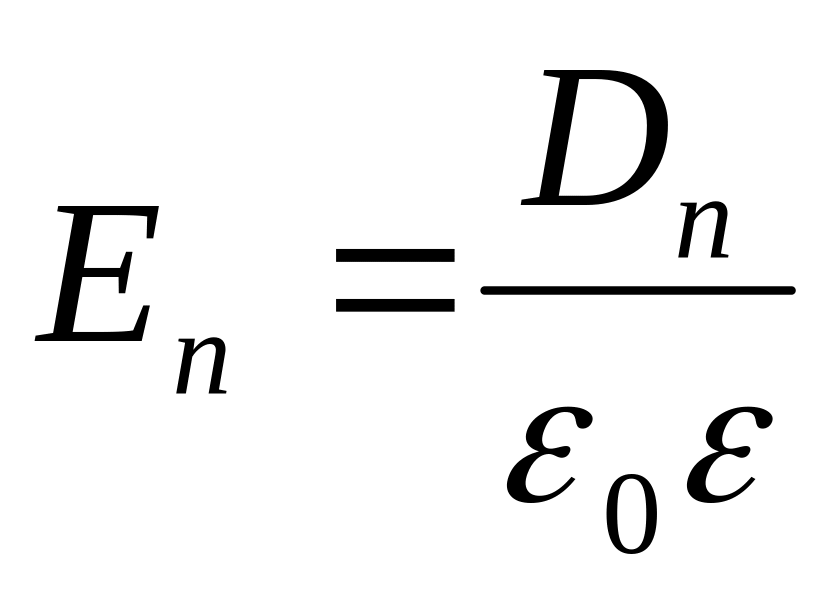, тангенциальная составляющая поля равна нулю в проводнике.

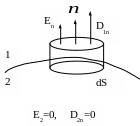
_1n

Рис.2.9

Из теоремы Гаусса для вектора запишем с учетом того, что Е₂=0 и D_2n=0

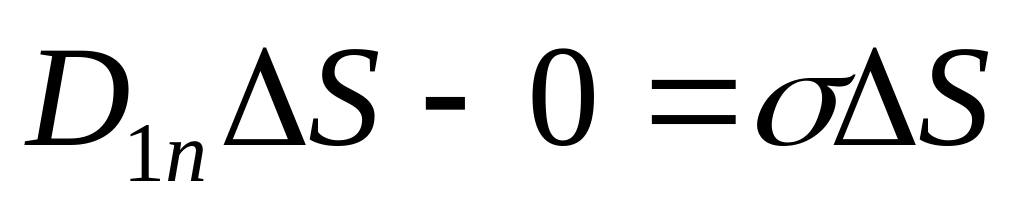, т.е., 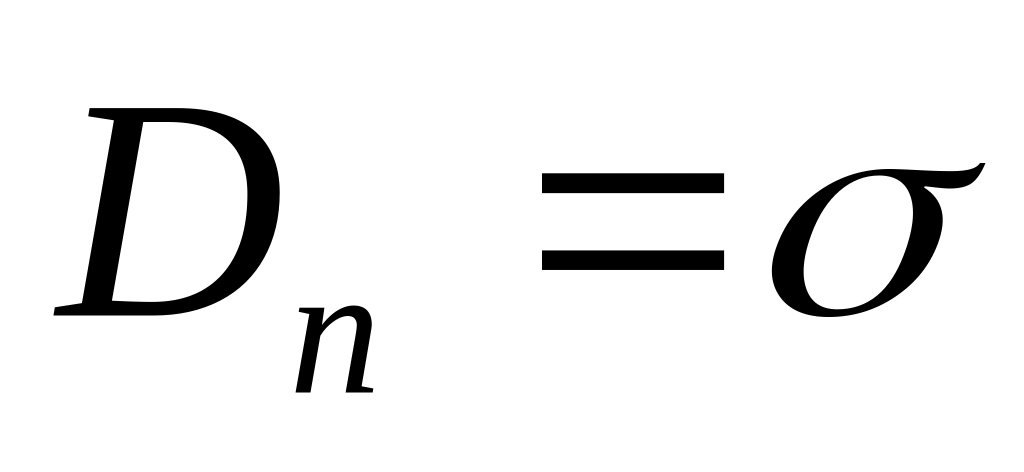. Подставляя это в , получим: .

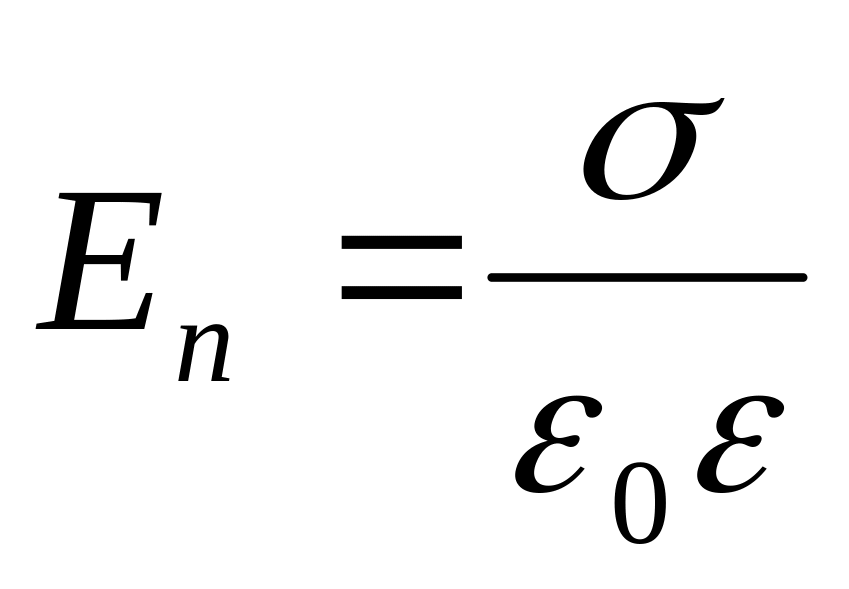А подставляя в и сокращая на /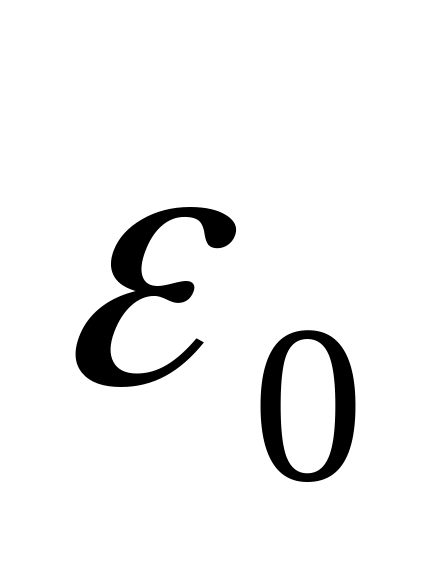 , получим:

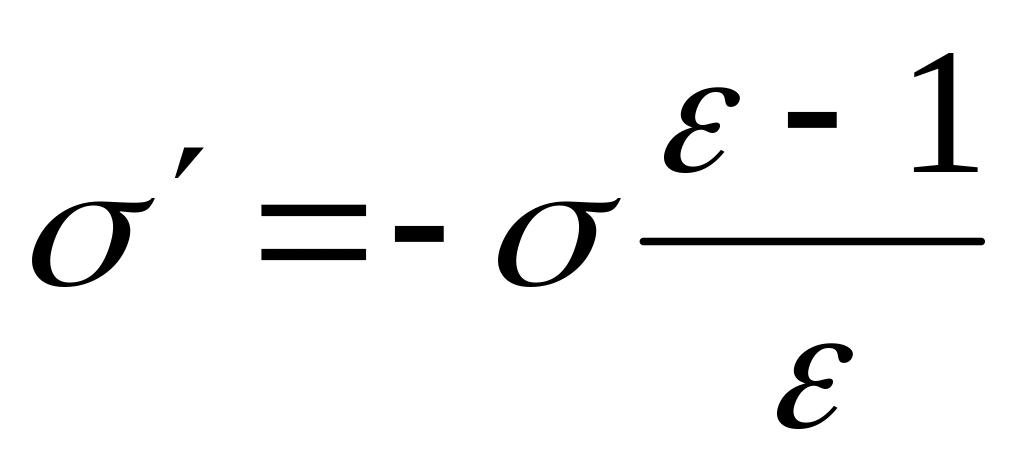, связанный поверхностный заряд, возникающий при поляризации имеет противоположный стороннему заряду знак и меньше его по величине в 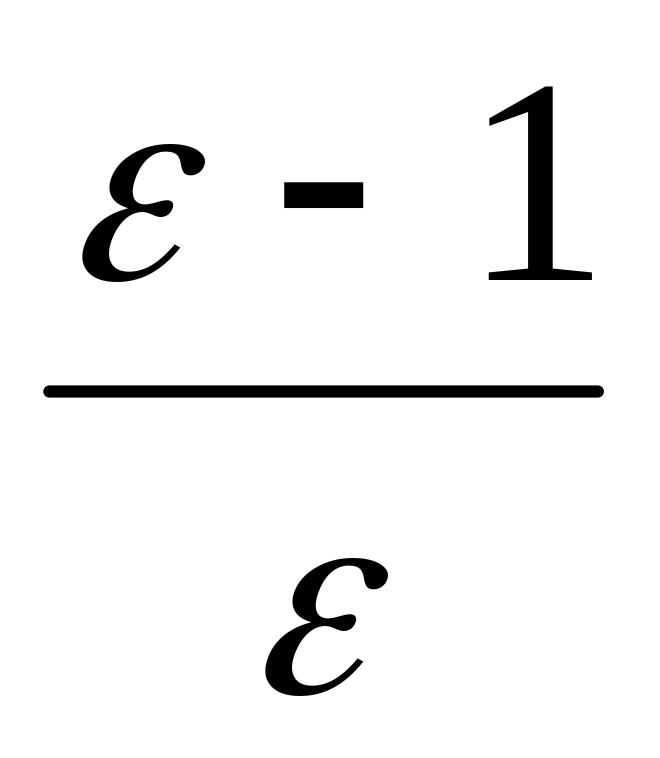раз.

2.11 Связь между объемным связанным зарядом диэлектрика и сторонним зарядом.

Когда 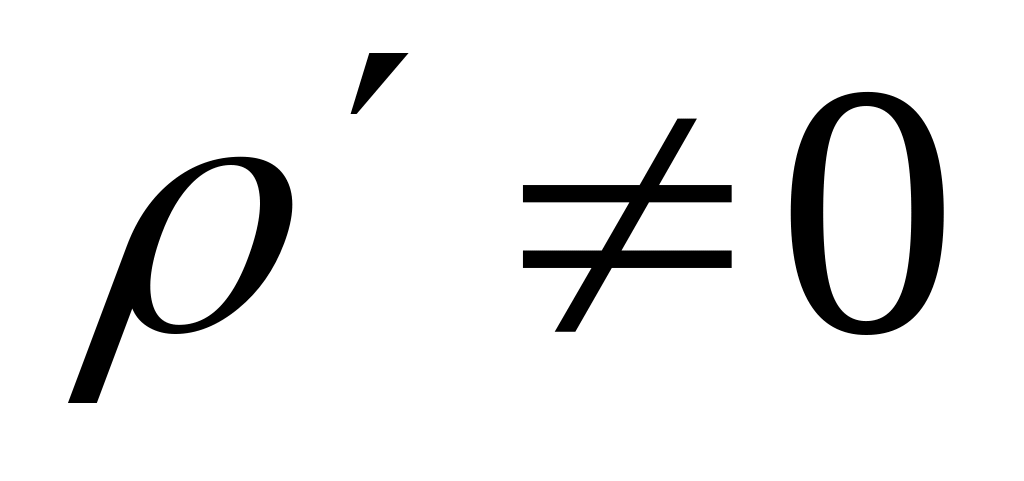формулу для дивергенции поля пишут в виде:

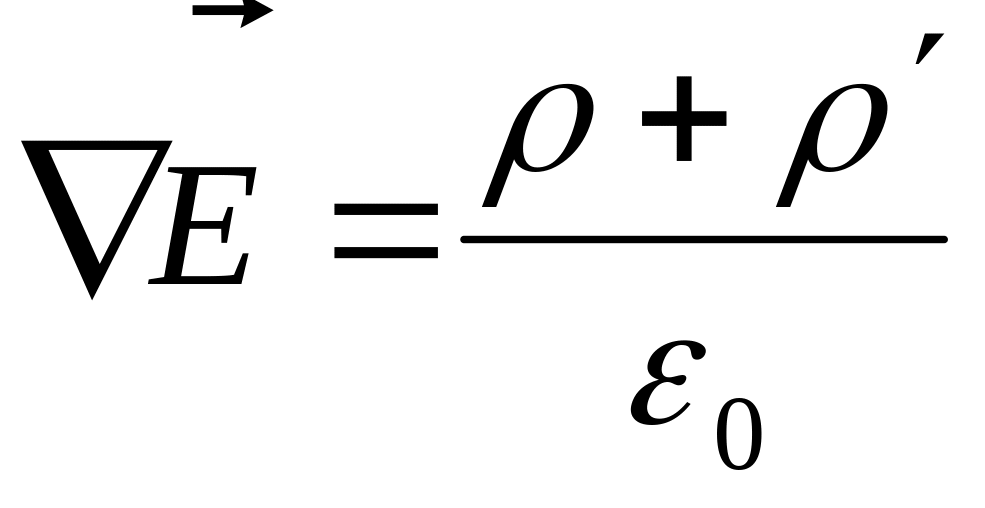
Отсюда можно найти связь между и . Для этого в теореме Гаусса для поляризованности 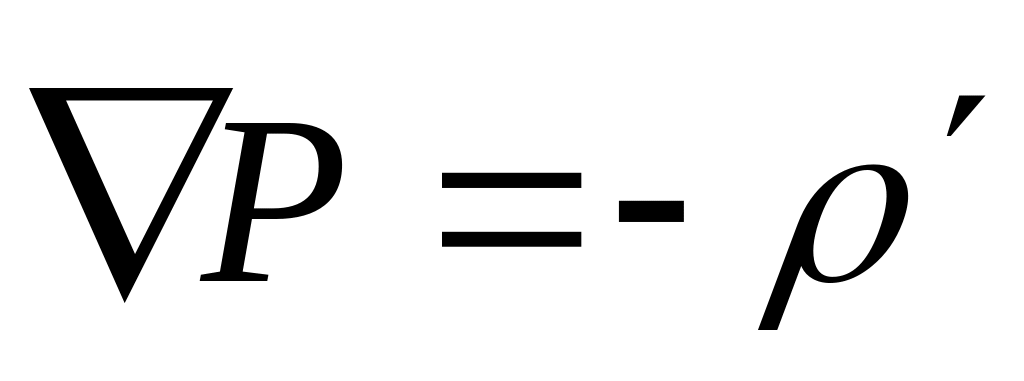заменим через диэлектрическую восприимчивость :

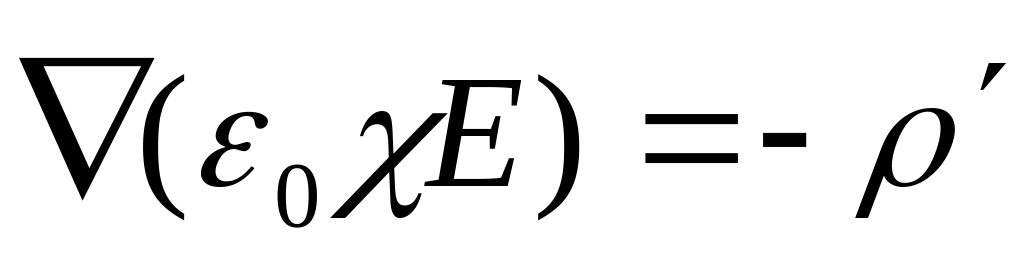, откуда 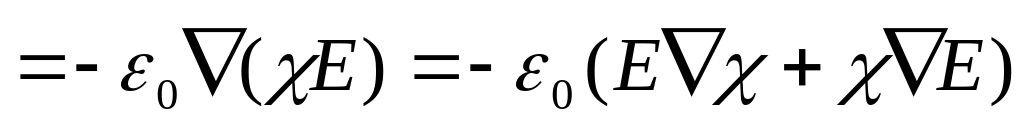. Подставив сюда значение , получим:

.

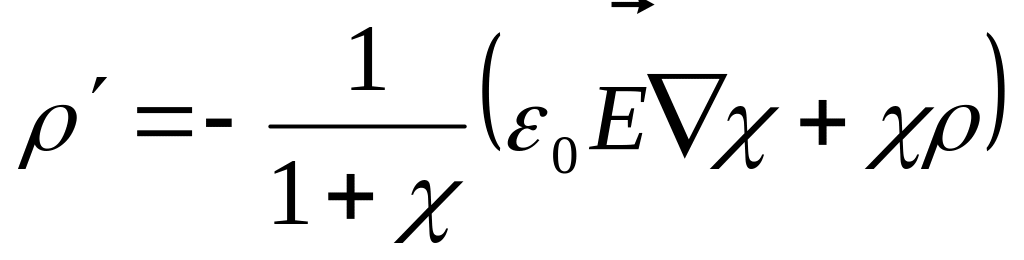Отсюда можно найти условия, при которых объемный заряд в диэлектрике будет отсутствовать, =0.

1. если 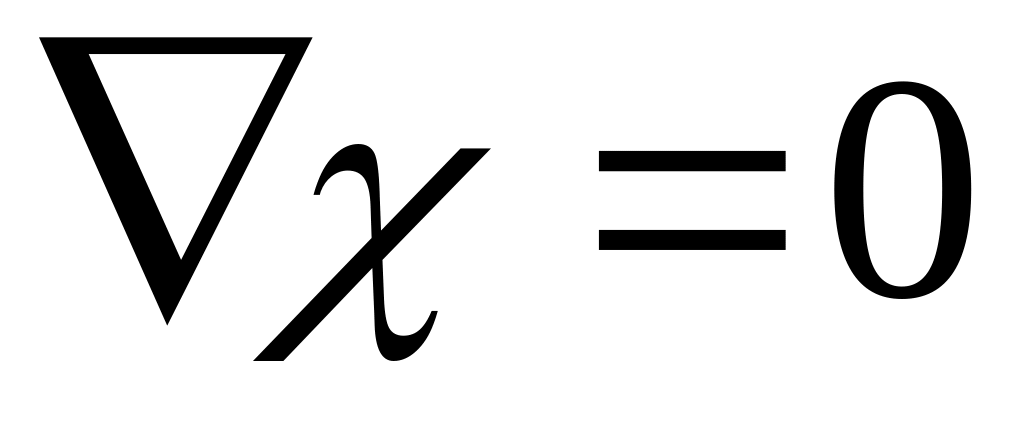, т.е., диэлектрик однородный, т.е., ;

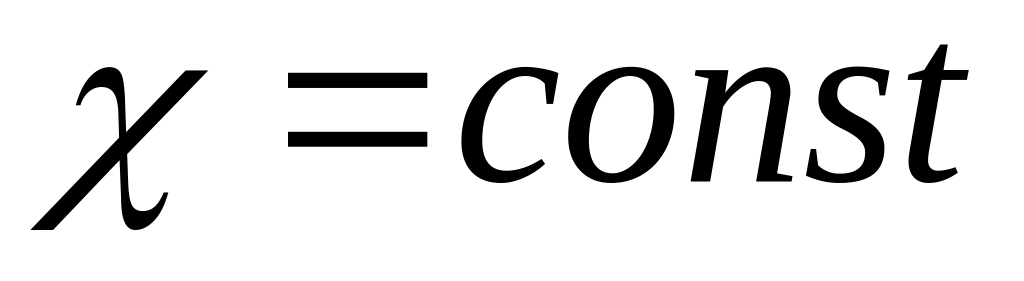2. если в данном месте диэлектрика (внутри) нет стороннего заряда, =0.

Таким образом, в однородном диэлектрике:

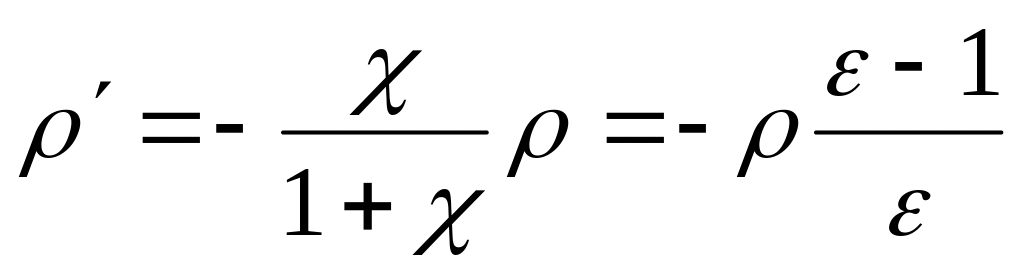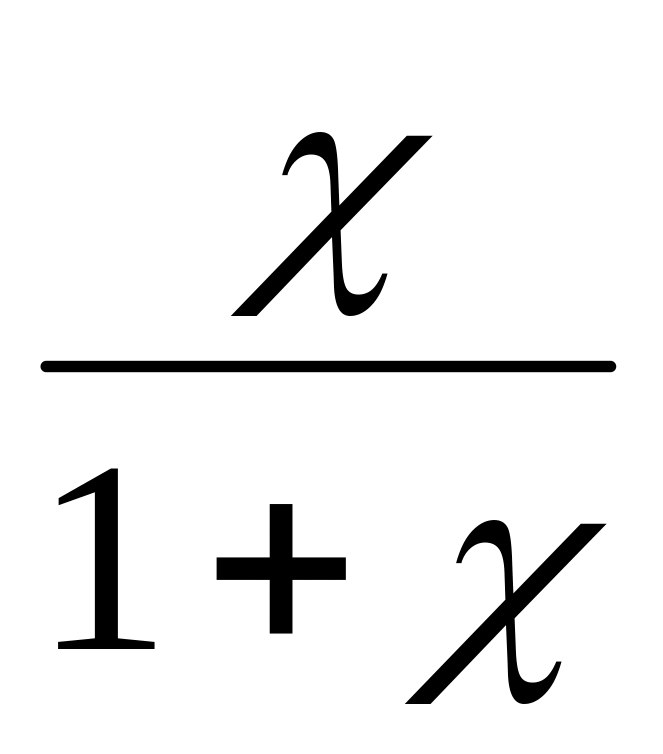, т.е. возникает связанный заряд противоположного знака и меньше стороннего в раз.