2.7 Вектор электрического смещения

Источниками электрического поля могут быть не только сторонние, но и связанные заряды, теорема Гаусса в этом случае имеет вид:

Эта формула мало что дает для нахождения поля в диэлектрике , т.к. в нее входит связанный заряд, который в свою очередь определяется этим же полем. Вычисление полей во многих случаях упрощается, если ввести вспомогательный вектор, поток которого через замкнутую поверхность зависит только от сторонних зарядов. Для этого заменим через вектор поляризованности из формулы , тогда: и далее: ()

Выражение в скобках и есть та величина, которая зависит только от сторонних зарядов . Ее называют электрическим смещением или индукцией электрического поля:

Если заменить вектор поляризованности , то

,

значит для изотропного диэлектрика пропорциональна , в анизотропном, где диэлектрическая проницаемость зависит от направления в веществе, векторы и неколлинеарны.

В соответствии с формулой для электрического смещения поля точечного заряда в вакууме можно записать:

.

Размерность электрического смещения как и поляризованности Кул/м².

Подставляя в выражение (), получим: - теорему Гаусса в дифференциальной форме для вектора .

Переход к интегральной форме осуществляется с помощью теоремы Остроградского-Гаусса и имеет вид:

- поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

Это выражение называют также обобщенной теоремой Гаусса.

В вакууме =0, поэтому и теорема Гаусса для вектора переходит в теорему для вектора :

П оле вектора можно изображать в виде линий электрического смещения, направление и густота которых определяются также как и для вектора . Линии вектора начинаются и заканчиваются на сторонних и связанных зарядах. Источниками поля являются только сторонние заряды, поэтому линии вектора начинаются и заканчиваются только на сторонних зарядах, через области, где есть связанные заряды, линии вектора проходят не прерываясь. На рис.2.4 показаны поля векторов , и для заряженного конденсатора с диэлектриком.

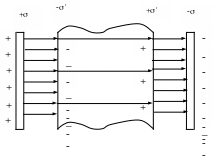
Рис.2.4

2.8 Теорема о циркуляции вектора

Как известно стационарное поле центральных сил консервативно, т.е., работа сил этого поля не зависит от формы пути, а зависит лишь от положения начальной и конечной точек пути. Этим свойством обладает и электростатическое поле – поле неподвижных зарядов. В таком поле элементарная работа по

перемещению единичного положительного заряда на перемещении равна , а вся работа сил на пути от точки 1 до точки 2 поля равна . Интеграл берется по некоторой линии и называется линейным. Из независимости этого интеграла от формы

пути следует, что по произвольному замкнутому пути он равен 0.

Интеграл по замкнутому пути называют циркуляцией вектора по контуру и обозначают как .

Итак, = 0, это утверждение называется теоремой о циркуляции

вектора . Для доказательства разобьем произвольный замкнутый путь на две части: 1а2 и 2в1, рис.2.5.

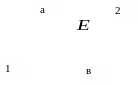
Т.к. работа не зависит от формы пути, то . С другой стороны, из математики известно,что Тогда, работа на всем пути: , значит .

Поле, обладающее свойством , называется потенциальным, значит, любое поле статических зарядов является потенциальным.

2.9 Условия для электростатического поля на границе двух диэлектриков

Вблизи поверхности двух диэлектриков векторы и должны удовлетворять определенным граничным условиям, которые вытекают из теоремы о циркуляции вектора и теоремы Гаусса для вектора :

, .

Пусть поле вблизи границы раздела в диэлектрике 1с ₁ равно , а в диэлектрике 2 с ₂ - . Векторы и лежат в одной плоскости с нормалью к поверхности раздела. Возьмем небольшой прямоугольный контур длины и ширины , который частично проходит в диэлектрике 1 и частично – в 2, рис.2.6. Длина контура выбирается такой, чтобы поле было постоянным в этой части диэлектрика, а ширина стремится к нулю. Тогда циркуляция вектора по замкнутому контуру должна быть по определению равна нулю:

, Здесь среднее значение поля на участках, перпендикулярных границе раздела диэлектрика на ширине , а и -проекции полей и на направление . При 0 последнее слагаемое мало и: или

=

Т.е., тангенциальные составляющие вектора оказываются одинаковыми по обе стороны границы раздела, не претерпевают скачка.

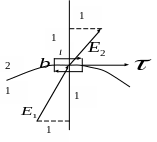
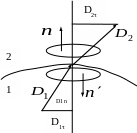
Рис.2.6 Рис.2.7

Условие для вектора получим, если возьмем на границе раздела замкнутую поверхность в виде цилиндра малой высоты с сечением таким, чтобы в его пределах = const, рис.2.7. Тогда, согласно теореме Гаусса, взяв обе проекции вектора на общую нормаль , получим:

Сократив на , получим:

,

т.е., нормальные составляющие вектора , в общем случае, претерпевают скачок, если на границе раздела есть сторонний заряд . При его отсутствии

т.е., нормальные составляющие вектора оказываются одинаковыми по обе стороны границы раздела.

Таким образом, если на границе раздела двух однородных изотропных диэлектриков сторонних зарядов нет, то при переходе этой границы составляющие векторов и изменяются непрерывно, без скачка. Составляющие и претерпевают скачок, это означает, что линии векторов и преломляются на границе, рис.2.8.

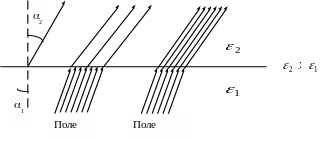
Рис.2.8

Учитывая, что и, соответственно, , а также, что , получим: и .

В диэлектрике с большим значением линии и составляют больший угол с нормалью к границе, на рисунке 2.8  . При переходе в диэлектрик с большей число линий вектора уменьшается, линии электрического смещения при этом сгущаются, а при переходе в диэлектрик с меньшей становятся реже.