1.2.4. Пример работы классического генетического алгоритма
Рассмотрим в качестве примера работы ГА процесс решения диофантова уравнения. Древнегреческий математик Диофант пытался найти ответ на вопрос: дано уравнение с целыми коэффициентами, имеет ли оно целое решение?
Пусть диофантово уравнение имеет вид:
FD(a,b,c,d) = a + 2b + 3c + 4d = 30,
где a, b, c и d - некоторые положительные целые.
Решение этого уравнения может быть найдено путем перебора вариантов значений a, b, c и d. Очевидно, что выполняется условие:
1 <= a,b,c,d <= 30,
Поэтому перебор здесь потребует не более 304=810000 вариантов. Конечно, для компьютера здесь не составляет труда найти решение прямым перебором, но при большем количестве переменных использование ГА помогает значительно сократить время поиска решения.
Хромосома в рассматриваемой задаче состоит из 4-х генов: a, b, c и d. Поскольку ген является целым числом, меньшим 30, для кодирования каждого гена можно использовать 5 битов. Тогда хромосома имеет вид, показанный на рис. 1.10.
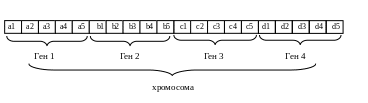Рис.
1.10. Кодирование решения диофантова
уравнения
Пусть для поиска решения используется маленькая популяция из 5 хромосом. Первоначально сгенерируем 5 случайных допустимых вариантов решений:
F(a,b,c,d) = a + 2b + 3c + 4d, a,b,с,d {1, 2, 3…30},
и свяжем с каждым вариантом значение ошибки решения:
= F(a,b,c,d) - FD(a,b,c,d)
В табл. 1.1 показаны варианты решений (в десятичном коде).
Таблица 1.1. Первое поколение хромосом и их пригодность
№ ( i ) |
Вариант (a,b,c,d) |
Ошибка () |
ОП |
1 |
(1,28,15,3) |
|114-30|=84 |
0.012 |
2 |
(14,9,2,4) |
|54-30|=24 |
0.042 |
3 |
(13,5,7,3) |
|56-30|=26 |
0.038 |
4 |
(23,8,16,19) |
|163-30|=133 |
0.0075 |
5 |
(9,13,5,2) |
|58-30|=28 |
0.036 |
Принцип работы ГА заключается в том, чтобы выживали хромосомы, имеющие меньшую ошибку решения. Поэтому относительную пригодность хромосомы можно описать формулой:
ОП = 1/
Для вычисления вероятности отбора хромосомы в будущую популяцию можно использовать формулу:
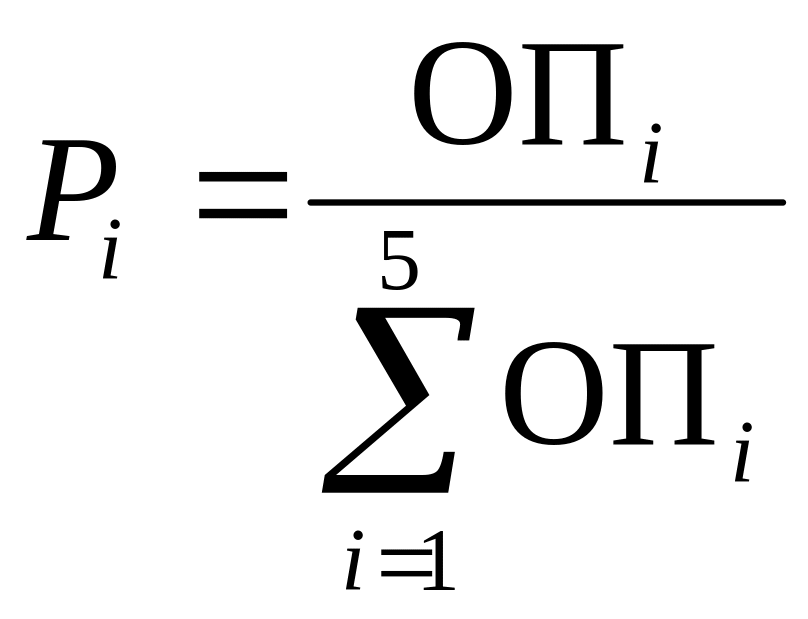
Результаты применения этой формулы представлены в табл.1.2.
Таблица 1.2. Вероятность отбора хромосом
i |
Pi |
Si |
1 |
0.012/0.135 = 0.09 |
9% |
2 |
0.042/0.135 = 0.31 |
31% |
3 |
0.038/0.135 = 0.28 |
28% |
4 |
0.0075/0.135 = 0.06 |
6% |
5 |
0.036/0.135 = 0.26 |
26% |
Для дальнейшего выбора хромосом можно использовать метод колеса рулетки. Каждой хромосоме соответствует сектор колеса Si (рис.1.11)
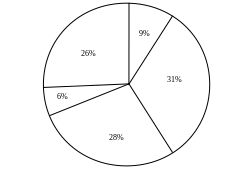
Рис. 1.11. Сектора колеса рулетки
После каждого вращения колеса выбирается какой-то сектор, то есть хромосома. После 10 вращений колеса могут быть отобраны 10 хромосом, из которых случайным образом формируются 5 пар для скрещивания. Пример показан в табл.1.3.
Таблица 1.3. Результаты отбора методом колеса рулетки
№ хромосомы «отца» |
№ хромосомы «матери» |
3 |
1 |
5 |
2 |
3 |
5 |
2 |
5 |
5 |
3 |
В соответствии с табл.1.3, самая плохая хромосома 4 ни разу не была отобрана для скрещивания. Хромосома 1 участвовала в скрещивании всего один раз, а хромосомы 2, 3 и 5 отбирались часто, поскольку имеют высокую OП.
Следующая генетическая операция – скрещивание. В своем классическом варианте операция скрещивания предполагает обмен «хвостов» хромосом после случайно выбранного гена хромосомы (точки скрещивания).
В табл. 1.4 приведен пример выполнения скрещивания.
Табл. 1.4. Скрещивание хромосом
точки скрещивания |
Хромосома - «отец» |
Хромосома - «мать» |
Хромосома-потомок |
1 |
(13 | 5,7,3) |
(1 | 28,15,3) |
(13,28,15,3) |
2 |
(9,13 | 5,2) |
(14,9 | 2,4) |
(9,13,2,4) |
3 |
(13,5,7 | 3) |
(9,13,5 | 2) |
(13,5,7,2) |
1 |
(14 | 9,2,4) |
(9 | 13,5,2) |
(14,13,5,2) |
2 |
(13,5 | 7, 3) |
(9,13 | 5, 2) |
(13,5,5,2) |
Пять хромосом-потомков образуют новую популяцию, для которой опять вычисляется ошибка (табл. 1.5).
Табл. 1.5. Новая популяция
i (№ хромосомы) |
Вариант (a,b,c,d) |
Ошибка () |
1 |
(13,28,15,3) |
|126-30|=96 |
2 |
(9,13,2,4) |
|57-30|=27 |
3 |
(13,5,7,2) |
|57-30|=22 |
4 |
(14,13,5,2) |
|63-30|=33 |
5 |
(13,5,5,2) |
|46-30|=16 |
Средняя ошибка решения в популяции потомков 39, в то время как у первоначальной популяции (табл. 1.1) этот коэффициент равнялся 59.
Последней выполняется генетическая операция мутации. Она может заключаться в замене одного из генов какой-нибудь хромосомы на случайное целое число от 1 до 30. Можно также давать случайное приращение одной из переменных, входящих в решение.
Повторяя генетические операции, можно добиться получения решения, т.е. хромосомы, которой соответствует нулевая ошибка.
Увеличение размера популяции оказывает положительное влияние на работу алгоритма, однако увеличивает вычислительные затраты.
Нужно заметить, что существует множество решений рассмотренной задачи, поэтому можно конкретизировать решение, например:
a + b + c + d → min