
- •Харківська державна академія залізничного транспорту
- •Диференціальне числення функцій однієї змінної та його застосування Методичні вказівки і завдання
- •Загальні рекомендації
- •Теоретичні питання Диференціальне числення функцій однієї змінної
- •Методичні вказівки
- •Завдання Завдання 1.
- •Завдання 2.
- •Завдання 3.
- •Завдання 4.
- •Завдання 5.
- •Список літератуРи
Завдання Завдання 1.
Знайти
похідні
![]() і в пунктах а), б), в) диференціали
dy
для заданих функцій:
і в пунктах а), б), в) диференціали
dy
для заданих функцій:
а)
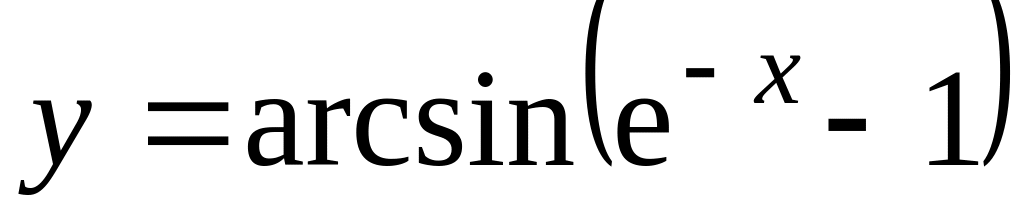 ;
б)
;
б)
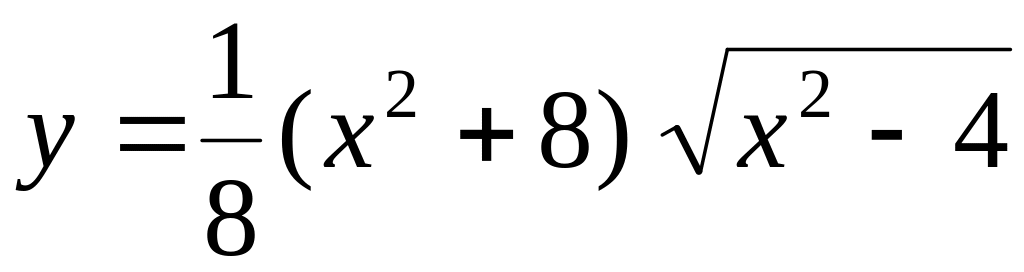 ;
;
в)
![]() ;
г)
y(arctgx)cosx;
д)
xy+ex+yx2–y2;
;
г)
y(arctgx)cosx;
д)
xy+ex+yx2–y2;
а)
 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
y=(sinx)5tgx;
д)
ln(1+y/x)=2x;
;
г)
y=(sinx)5tgx;
д)
ln(1+y/x)=2x;
а) y=5e-3tg(x/3); б)
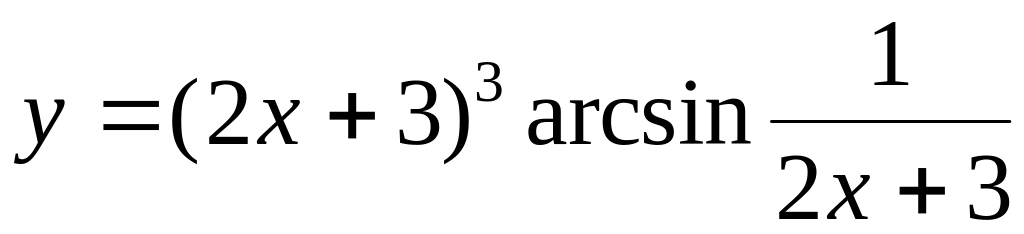 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
x+yxsiny–ysinx;
;
д)
x+yxsiny–ysinx;
а)
 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
tg(xy)=2y;
;
д)
tg(xy)=2y;
а)
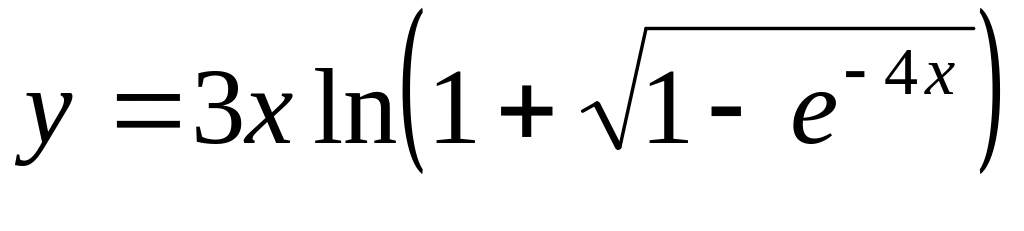 ;
б)
;
б)
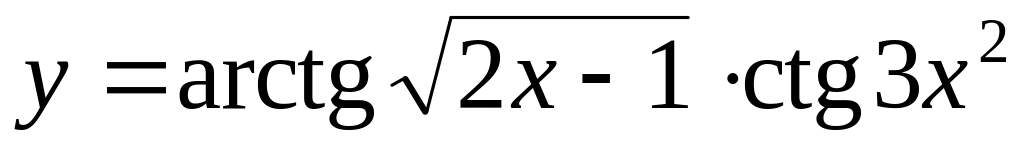 ;
;
в)
![]() ;
г)
y=(x2–1)cosx;
д)
x2+y=ycosx–xcosy;
;
г)
y=(x2–1)cosx;
д)
x2+y=ycosx–xcosy;
а)
 ;
б)
y
sin2x·ctg2
3x;
;
б)
y
sin2x·ctg2
3x;
в)
![]() ;
г) y
(x+2)tgx;
д)
sin(xy–8)
y2+x2;
;
г) y
(x+2)tgx;
д)
sin(xy–8)
y2+x2;
а)
 ;
б)
y=xln(1+ctg2x);
;
б)
y=xln(1+ctg2x);
в)
![]() ;
г) y
= (x2+1)arcsinx;
д) y
= x+3cosy;
;
г) y
= (x2+1)arcsinx;
д) y
= x+3cosy;
а) y=sin(x/3)lnsin(x/3); б)
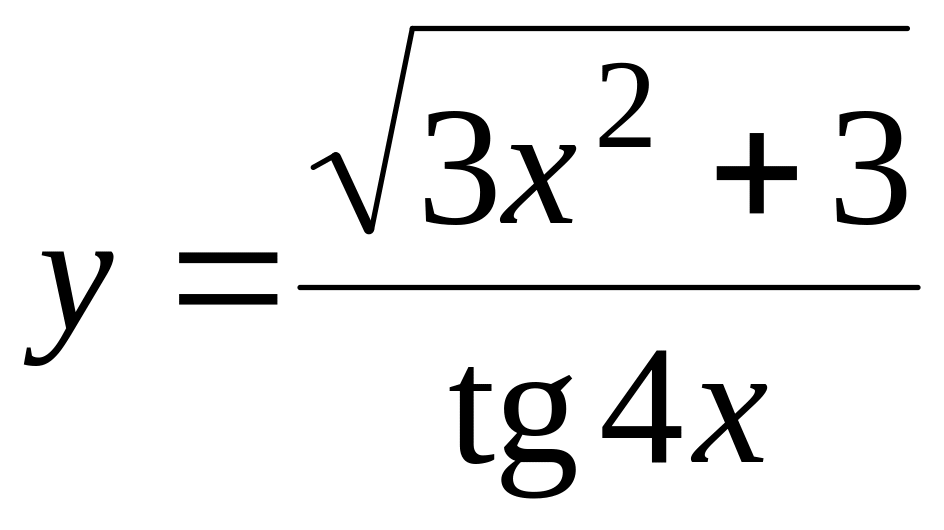 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
y2+tgx+ctgxy
= 0;
;
д)
y2+tgx+ctgxy
= 0;
а)
 ;
б)
;
б)
 ;
;
в) y
= tg(e2x-1);
г)
y =
![]() ;
д)
;
д)
![]() ;
;
а)
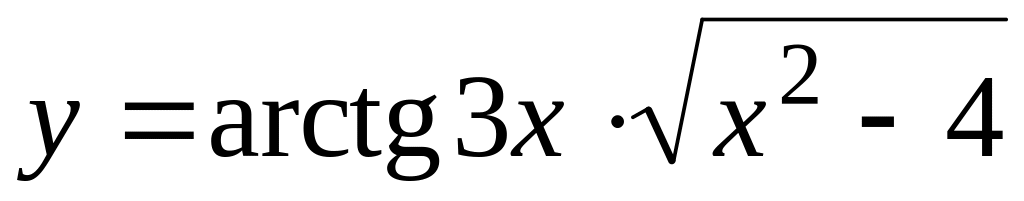 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
y+cosx+sin(x/y)
= 0;
;
д)
y+cosx+sin(x/y)
= 0;
а)
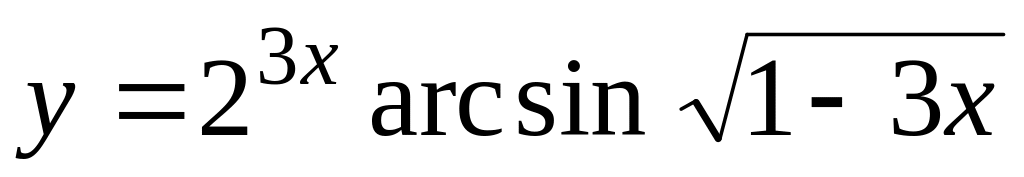 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
xy+sin(x+y)
= 0;
;
д)
xy+sin(x+y)
= 0;
а)
 ;
б)
;
б)
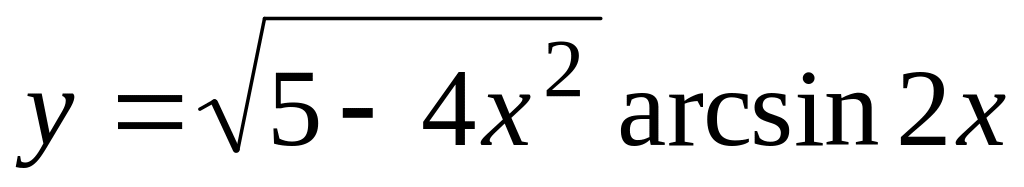 ;
;
в)
![]() ;
г) y
= (tgx2)lnx;
д)
xy+sin(x/y)
= 0;
;
г) y
= (tgx2)lnx;
д)
xy+sin(x/y)
= 0;
а)
 ;
б) y
= (e3x
+7x)4;
;
б) y
= (e3x
+7x)4;
в)
![]() ;
г) y
= (tgx2)sinx;
д)
x+y+cos(y/x)=0;
;
г) y
= (tgx2)sinx;
д)
x+y+cos(y/x)=0;
а) y = ln(3+ctg2x); б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
x+y2+tg(xy)
= 0;
;
д)
x+y2+tg(xy)
= 0;
а)
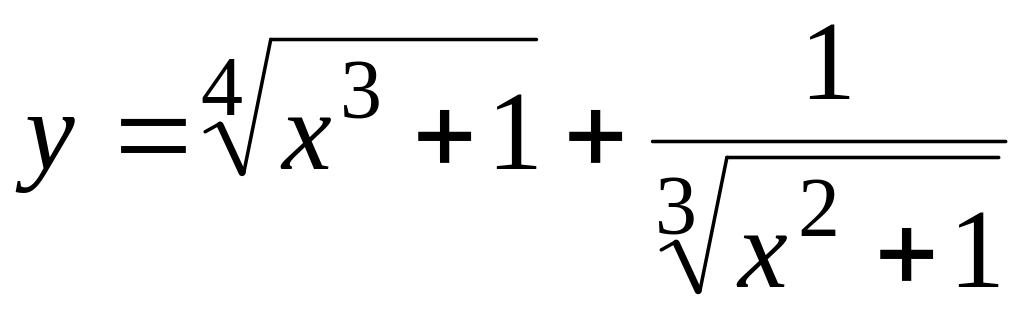 ;
б) y
= (esin2x+4x)4;
;
б) y
= (esin2x+4x)4;
в)
![]() ;
г) y
= (ctg2x)sinx;
д)
x2+y+ctg(xy)
= 0;
;
г) y
= (ctg2x)sinx;
д)
x2+y+ctg(xy)
= 0;
а)
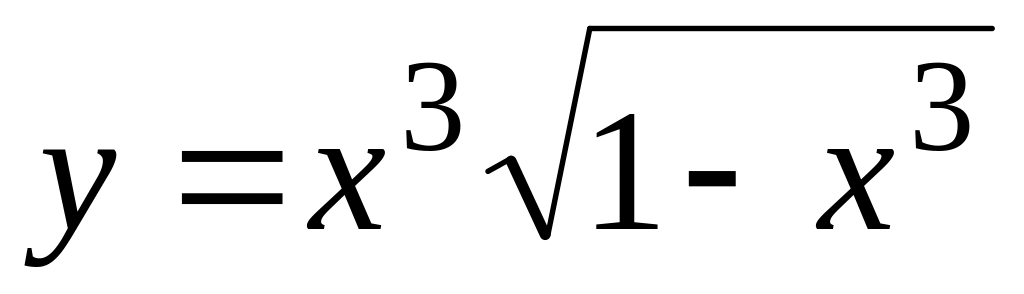 ;
б)
;
б)
 ;
;
в) y
= arctg(e3x);
г)
![]() ;
д) xy
+ ch(xy)
= 0;
;
д) xy
+ ch(xy)
= 0;
а)
 ;
б)
;
б)
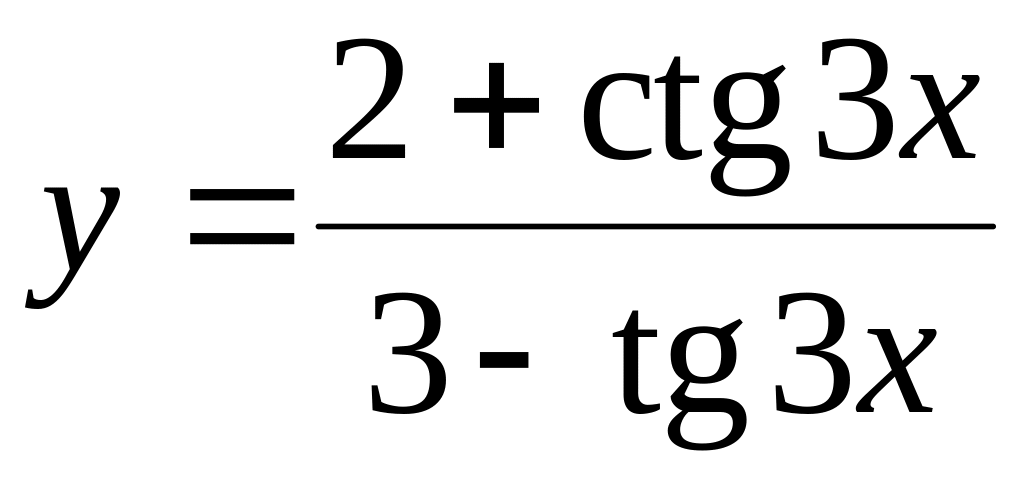 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
th(x/y)=7x;
;
д)
th(x/y)=7x;
а)
 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
2x–y–ch(x/y)=0;
;
д)
2x–y–ch(x/y)=0;
а)
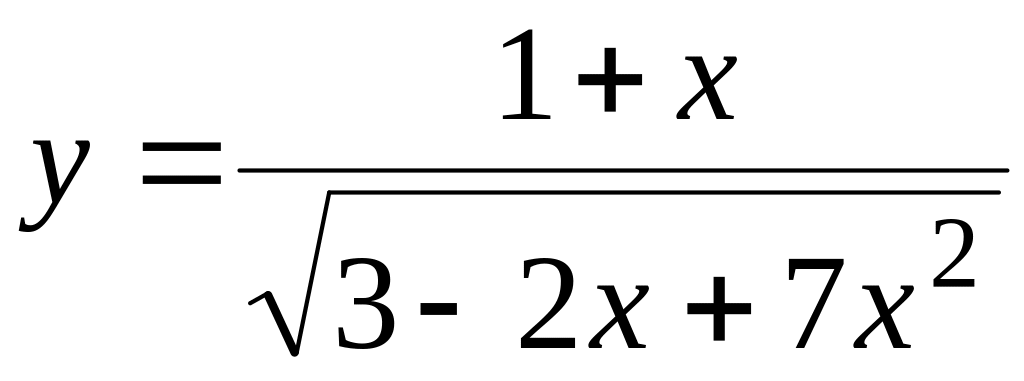 ;
б) y
= cos2x–2xsin2x;
;
б) y
= cos2x–2xsin2x;
в)
![]() ;
г)
;
г)
![]() ;
д) ychx
= sh(xy);
;
д) ychx
= sh(xy);
а) y=2ctg3(x3+5); б)
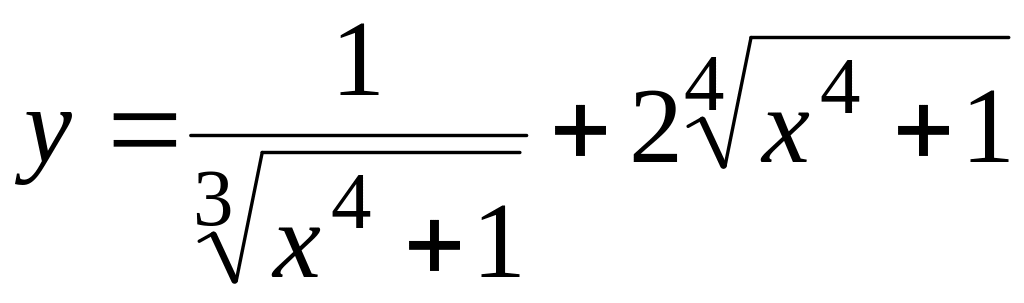 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) y3
– x3
+ 6xy = 0;
;
д) y3
– x3
+ 6xy = 0;
а)
 ;
б)
y=(x3–4x)lncos(3x+7);
;
б)
y=(x3–4x)lncos(3x+7);
в)
![]() ;
г)
y=(shx)chx;
д) 3x/y
= arctg(x2+y2);
;
г)
y=(shx)chx;
д) 3x/y
= arctg(x2+y2);
а)
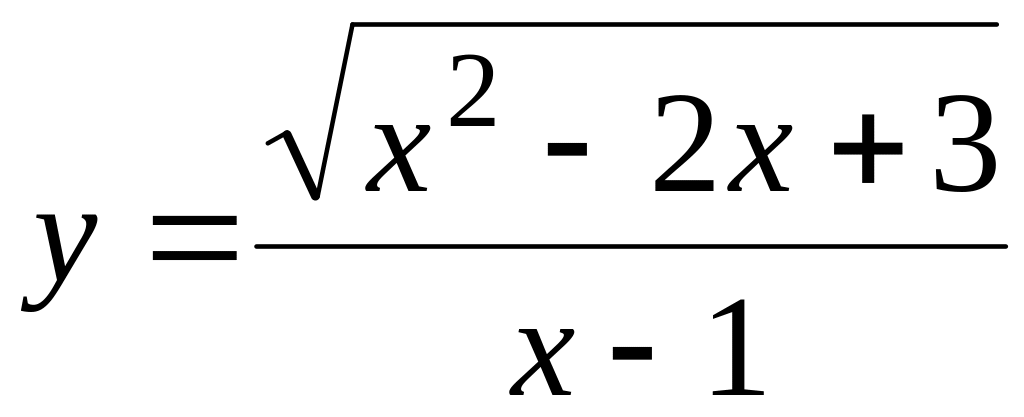 ;
б)
;
б)
 ;
;
в) y=(etg2x+x)4; г) y=(arctg2x)tgx; д) y – x + th(xy) = 0;
а)
 ;
б) y
= (earcsin3x+5)3;
;
б) y
= (earcsin3x+5)3;
в)
y=sin2x2ln(x2+1);
г)
![]() ;
д) (ex
–2)(ey
–3)
=
5;
;
д) (ex
–2)(ey
–3)
=
5;
а)
 ;
б) y
= ctg
ln(3x2+4);
;
б) y
= ctg
ln(3x2+4);
в)
![]() ;
г)
;
г)
![]() ;
д) lny
= arctg(x/y);
;
д) lny
= arctg(x/y);
а)
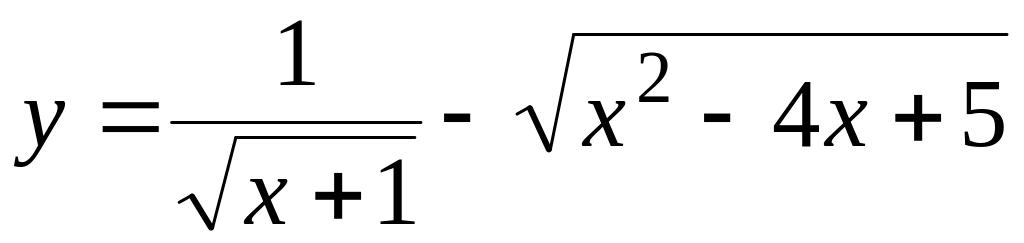 ;
б) y
= (earctg5x+5)4;
;
б) y
= (earctg5x+5)4;
в) y = ln tg(5x+2); г) y = (thx)chy; д) y = xexy;
а) y = (sin2x+tg2x)3; б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) x3
+ y3
= th(xy);
;
д) x3
+ y3
= th(xy);
а) y=(2x–5)3 ln(4x2–25); б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) x2
– y2
= ch(xy);
;
д) x2
– y2
= ch(xy);
а)
 ;
б)
;
б)
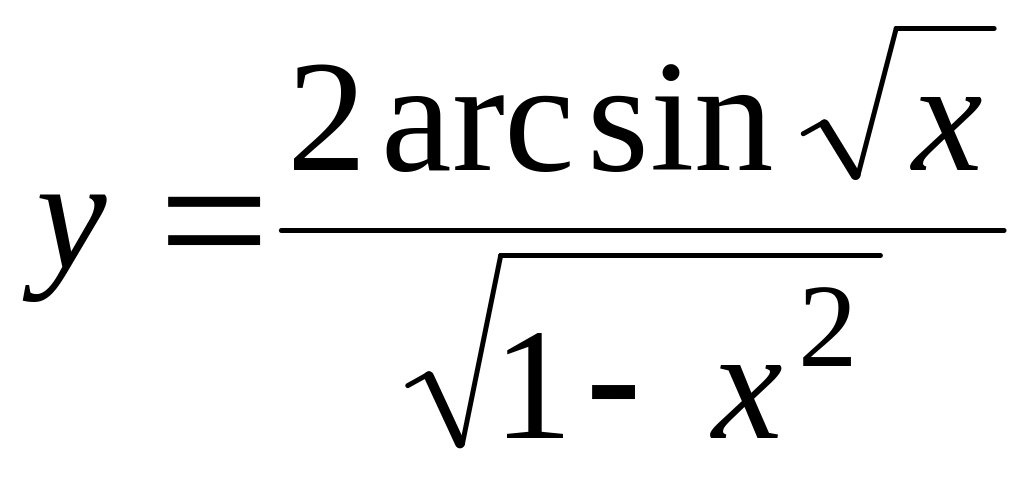 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) xy
= ch(x2
+ y2);
;
д) xy
= ch(x2
+ y2);
а) y=5sin4xtg(x2+4); б)
 ;
в)
;
в)
 ;
;
г)
![]() ;
д) exy
= sh(x+y);
;
д) exy
= sh(x+y);
а)
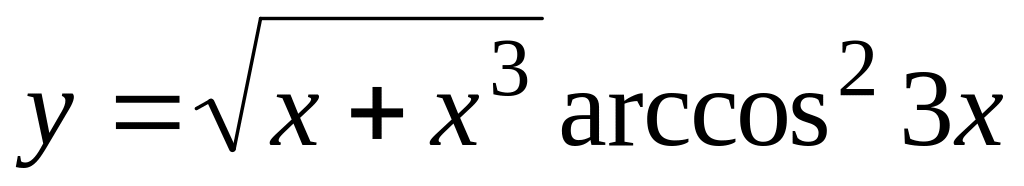 ;
б)
;
б)
 ;
в)
;
в)
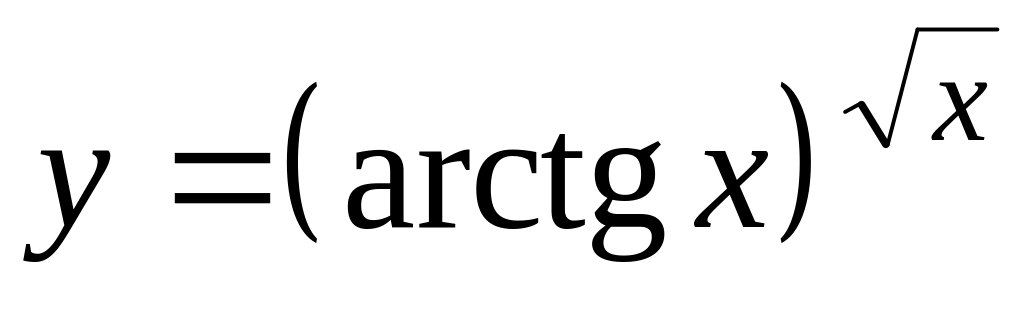 ;
;
г) y = ln cos(5x2–3); д) ch(x2 – y2)= x – y;
а)
 ;
б)
;
б)
 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д) ex–y
= x2
+y2;
;
д) ex–y
= x2
+y2;
а) ; б) ; в) ;
г) ; д) 1-cos (xy)=sin (x+y).
Завдання 2.
Знайти рівняння дотичних прямих і нормалей до графіків функцій, а також їхні кривини в заданих точках:
а) y=(4x–x2)/4, x0=2; б) x=cos(t/2), y=t/–ctgt, t0=/3;
а) y=2x2+3x–1, x0=–2; б) x=cos(t/4), y=t/+tgt, t0=;
а) y=x–x3, x0=–1; б) x=t3 –t2, y=cos2t, t0=1/3;
а) y=x2+8
 –32,
x0=4; б) x=t2
+1,
y=sin4
t,
t0=1/4;
–32,
x0=4; б) x=t2
+1,
y=sin4
t,
t0=1/4;а) y=x+
 ,
x0=1; б) x=arctg
t,
y=t2+4,
t0=1;
,
x0=1; б) x=arctg
t,
y=t2+4,
t0=1;а) y=(1+ )/(1– ), x0=4; б) x=tgt, y=cost, t0=1/4;
а) y=4x2–3x+1, x0=1; б) x=cos2t, y= t2+1, t0=/3;
а) y=x–6
 ,
x0=8; б) x=sin2t,
y=
cos2t,
t0=/4;
,
x0=8; б) x=sin2t,
y=
cos2t,
t0=/4;а) y=
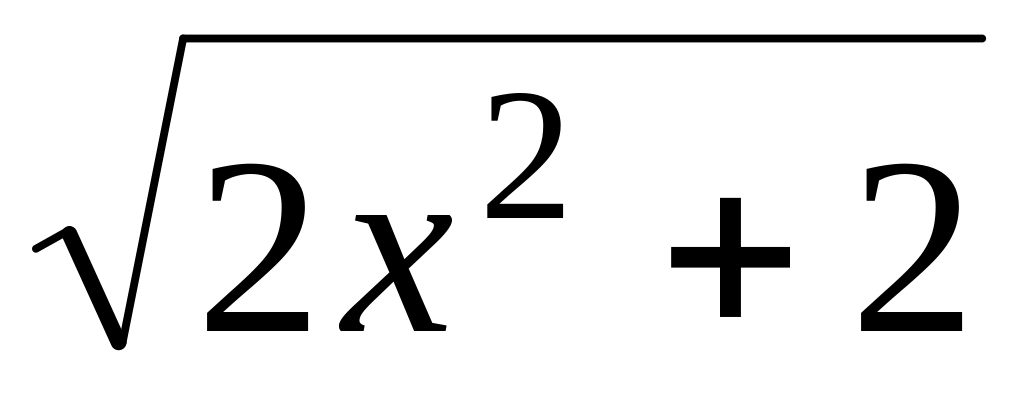 ,
x0=–1; б) x=tg2t,
y=1/t,
t0=1/3;
,
x0=–1; б) x=tg2t,
y=1/t,
t0=1/3;а) y=(x5+1)/(x4+1), x0=1; б) x= ctg2t, y=t-2, t0=1/6;
а) y=3 –6 , x0=1; б) x=1/sint, y=1/t, t0=/4;
а) y=2x/(x2+1), x0=–2; б) x=tg(t/3), y=t3–3, t0=;
а) y=(1+3x2)/(3+x2), x0=–1; б) x=ch t, y=sh t, t0=ln3;
а) y=
 ,
x0=9; б) x=1/cost,
y=2/t2,
t0=/4;
,
x0=9; б) x=1/cost,
y=2/t2,
t0=/4;
а) y=
 ,
x0=8; б) x=t2
+4t,
y=5t4–3t,
t0=2;
,
x0=8; б) x=t2
+4t,
y=5t4–3t,
t0=2;а) y=x2–8 , x0=4; б) x=sh(t/2), y=ch(t/2), t0=ln4;
а) y=9–
 ,
x0=4; б) x=1+
,
x0=4; б) x=1+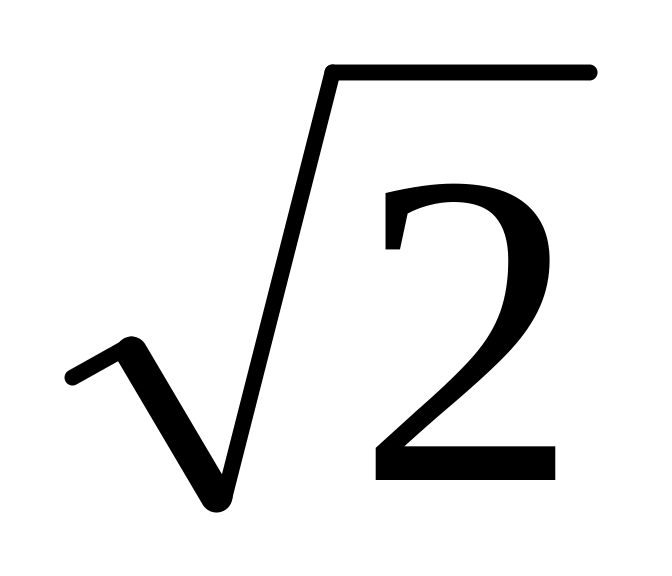 cost,
y=2–
sint,
t0=/4;
cost,
y=2–
sint,
t0=/4;а) y=x2–8x+22, x0=–2; б) x=e-2t, y=e3t, t0=1;
а) y=8 +18, x0=–8; б) x=2cos3 t, y=3sin2 t, t0=/4;
а) y=x2–3x+6, x0=3; б) x=5sin t, y=6cos2 t, t0=/3;
а) y= (x+2)/(x2–2), x0=1; б) x=t2 +3t, y=5t2, t0=2;
а) y= (x2–6)/(x+1), x0=2; б) x=5t – t3, y=3t2, t0=2;
а) y=–2(x8+2), x0=1; б) x=1+ln t3, y=–3+ln t2, t0=e;
а) y= (x2+9)/(1–2x2), x0=1; б) x=cos3 2t, y=sin2 3t, t0=/12;
а) y= 1/(3x+2), x0=2; б) x=3cos2 2t, y=cos2 3t, t0=/6;
а) y=(3x–2x3)/3, x0=2; б) x=cos2 (t/4), y=(t2+2t)/, t0=;
а) y=
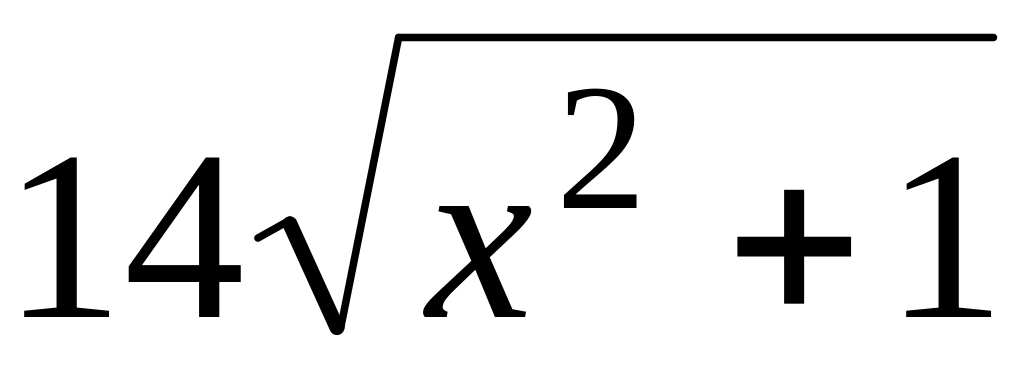 ,
x0=0; б) x=2tg
t,
y=3ctg
t,
t0=/3;
,
x0=0; б) x=2tg
t,
y=3ctg
t,
t0=/3;а) y=3/x+
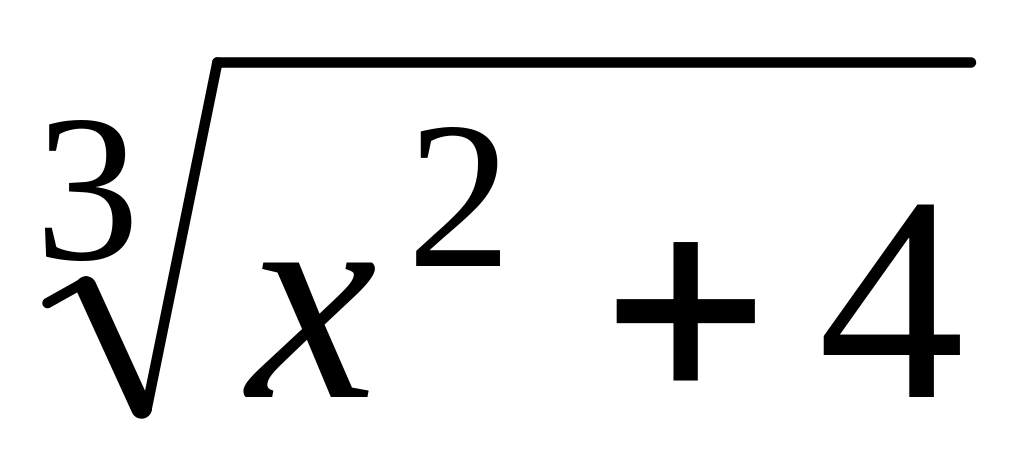 ,
x0=2; б) x=sin2
t,
y=t2+1,
t0=/4;
,
x0=2; б) x=sin2
t,
y=t2+1,
t0=/4;а) y= x2
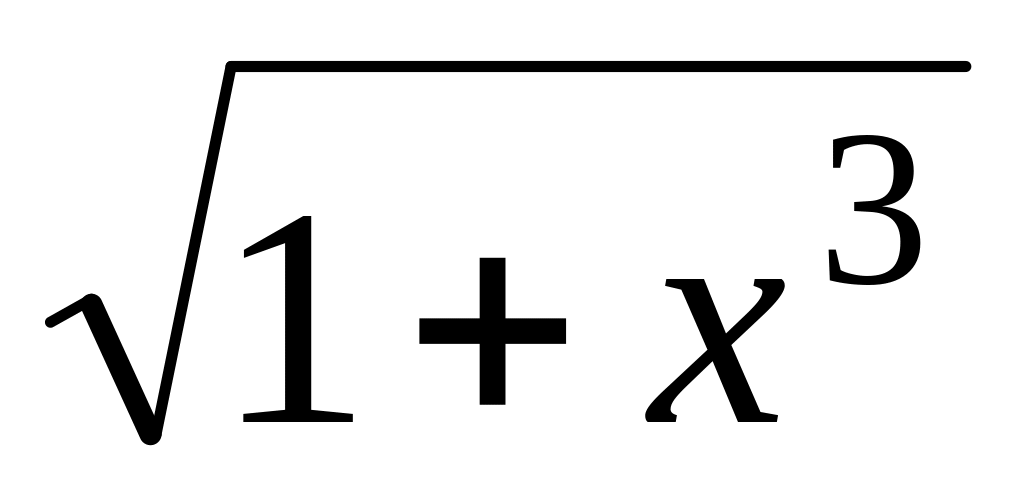 ,
x0=1; б) x=
t2–1,
y=cos3
t,
t0=/4;
,
x0=1; б) x=
t2–1,
y=cos3
t,
t0=/4;а) y=exsinx, x0=0; б) x=3sin2 (t/4), y=2cos2 (t/6), t0=;
а) y=
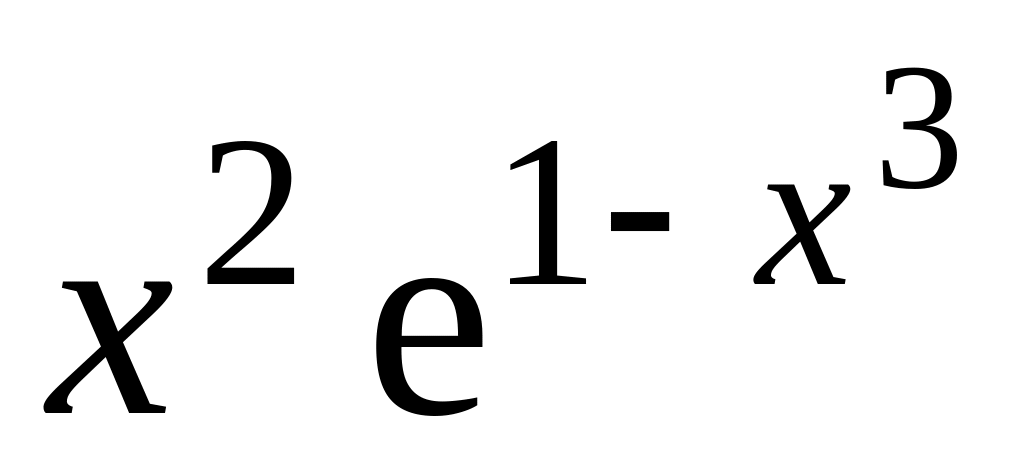 ,
x0=1; б) x=th2
t,
y=cth2
t,
t0=ln2.
,
x0=1; б) x=th2
t,
y=cth2
t,
t0=ln2.
