
- •Основні формули та алгоритми:
- •З апишіть формулу обчислення визначника другого порядку:
- •Запишіть формулу обчислення визначника третього порядку:
- •Роздатковий матеріал №1
- •1. Обчислити визначники:
- •2. Розв’язати системи за правилом Крамера:
- •3. Розв’язати системи методом Гауса:
- •4.Обчислити визначники
- •Основні формули та алгоритми.
- •Роздатковий матеріал №2
- •Основні формули та алгоритми.
- •Роздатковий матеріал №3
- •Основні формули та алгоритми.
- •Роздатковий матеріал №4
- •Основні формули та алгоритми.
- •Роздатковий матеріал №5
- •Основні формули та алгоритми.
- •Роздатковий матеріал №6
- •Основні формули та алгоритми.
- •Роздатковий матеріал №7
- •Основні формули та алгоритми.
- •Роздатковий матеріал №8
- •Основні формули та алгоритми.
- •Роздатковий матеріал №9
- •Основні формули та алгоритми.
- •Роздатковий матеріал №10
- •2. Використати метод підстановки для знаходження невизначених інтегралів:
- •3. Обчислити визначені інтеграли:
- •Основні формули та алгоритми.
- •Запишіть основні властивості визначеного інтегралу:
- •Запишіть формулу Ньютона-Лейбніца: Роздатковий матеріал №11
- •Основні формули та алгоритми.
- •Роздатковий матеріал №12
Основні формули та алгоритми.
Невизначеним інтегралом від функції f (x) називається
Запишіть властивості невизначеного інтегралу:
![]()
![]()
![]()
![]()
Заповніть таблицю інтегралів:

4. Запишіть формулу Ньютона-Лейбніца:
Роздатковий матеріал №10
Знайти невизначені інтеграли методом розкладу.
1.
2.
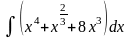
3.
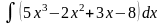
4.

5.
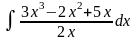
6.
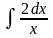
7.

8.

9.
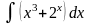
10.
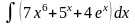
11.

12.
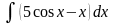
13.
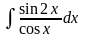
14.
15.

16.
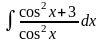
17.
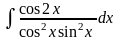
18.
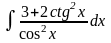
2. Використати метод підстановки для знаходження невизначених інтегралів:
19.
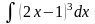
20.
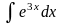
21.
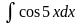
22.

23.

24.
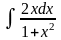
25.
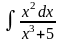
26.
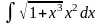
3. Обчислити визначені інтеграли:
27.
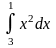
28.

29.

30.
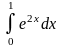
Домашня робота
1.
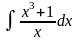 2.
2.
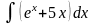 3.
3.
 4.
4.

5.
 6.
6.

Практичне заняття №11
Тема заняття: Застосування визначеного інтегралу.
Мета заняття: Вміти застосовувати визначений інтеграл до обчислення площ плоских фігур.
Література
№ |
Назва підручника |
Автори |
Сторінки до теми |
1 |
Математика |
В.М.Лейфура, Г.І. Городницький, Й.Й.Файст |
с. 491-544 |
2 |
Математика |
В.Т.Лисичкин, И.Л. Соловейчик |
с. 290-355 |
3 |
Математика для техникумов |
И.И. Валуцэ, Г.Д. Дилигул |
с. 247-310 |
Основні формули та алгоритми.
Запишіть основні властивості визначеного інтегралу:
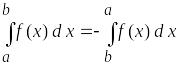
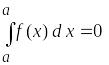
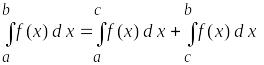
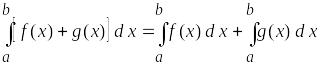
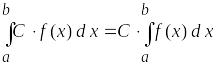
Запишіть формулу Ньютона-Лейбніца: Роздатковий матеріал №11
Обчислити визначені інтеграли:
1.
2.

Обчислити площі фігур, обмежені лініями:
а)
Площа
фігури, що знаходиться над віссю Ох
обчислюють за формулою:

5.
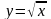 ,
,
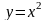
6.
 ,
х=16,
х=25, у=0.
,
х=16,
х=25, у=0.
7. ху=6, х+у-7=0
б)
Площа
фігури, що знаходиться повністю або
частково під віссю Ох обчислюють за
формулою:
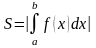
8. у=-2х, у=0, х=3.
9. у=4х-х2, у=0, х=5
в)
Площа
фігури, що прилягає до осі Оу обчислюють
за формулою:
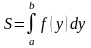
11. у=х2, у= 4, у=9, х=0
г) Якщо плоскі фігури розміщені симетрично, то обчислюють половину площі і подвоюють результат.
12. у=х2+1, х=-2, х=2, у= 0
Домашня робота Обчислити площу фігури обмежену лініями
1.х-2у+4=0, х+у-5=0, у=0 2. у=-х2+5, у= х+3 3. у=х3, у= 8, х=0
Практичне заняття № 12
Тема заняття: Розв’язування диференціальних рівнянь першого порядку. Розв’язування задач, які приводять до диференціальних рівнянь.
Мета заняття: Вміти розв’язувати диференціальні рівняння з відокремленими та відокремлюваними змінними.
Література
№ |
Назва підручника |
Автори |
Сторінки до теми |
1 |
Математика |
В.М.Лейфура, Г.І. Городницький, Й.Й.Файст |
с. 545-563 |
2 |
Математика |
В.Т.Лисичкин, И.Л. Соловейчик |
с. 369-384 |
3 |
Математика для техникумов |
И.И. Валуцэ, Г.Д. Дилигул |
|
