Основні формули та алгоритми.

1. Записати алгоритм графічного розв^/язку системи лінійних нерівностей:

-

-

-

-

2. Якщо нерівність строга (<; >), то область розв^/язків __________________, пряму будуємо______________________лінією.

3. Якщо нерівність не строга (≤; ≥), то область розв^/язків_________________, пряму будуємо______________________лінією.

4. Якщо півплощини не мають спільних точок, то областю розв'язків є _____________________, а система нерівностей називається ______________.

5. Якщо півплощини мають спільні точки, то областю розв'язків є ___________________________________________________________________, а система нерівностей називається _________________.

6. Цільовою називається функція

Роздатковий матеріал №4

Завдання 1. Побудувати області, координати яких задовольняють нерівностям:

а) у<2-x , х>-2, y>-2.

б) y>2-x, x<4, y<0.

_в)

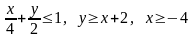
Завдання 2. Побудувати область розв’язків системи лінійних нерівностей:

а) ,

б)

в)

Завдання 3. Знайти невід’ємні значення змінних х₁ та х₂ , які задовольняють систему нерівностей і надають найбільшого (найменшого) значення цільовій функції f=x₁+2x₂.

Домашня робота: Побудувати область розв’язків системи лінійних нерівностей: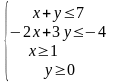

Практичне заняття № 5

Тема заняття: Знаходження границь функцій. Дослідження функцій на неперервність.

Мета заняття: Розширити і вдоконалити навички знаходження границь функцій, розкриття невизначеностей та застосування першої та другої чудової границі.

Література

№	Назва підручника	Автори	Сторінки до теми
1	Математика	В.М.Лейфура, Г.І. Городницький, Й.Й.Файст	c.156-207, 358-383
2	Математика	В.Т.Лисичкин, И.Л. Соловейчик	c. 164-196
3	Математика для техникумов	И.И. Валуцэ, Г.Д. Дилигул	c. 172-204

Основні формули та алгоритми.

1.Запишіть основні властивості функцій:

2. Запишіть елементарні функції:

3. Границею функції f (x) у точці а (при х  а) називають

4. Основні теореми про границі функцій:

- границя суми функцій дорівнює

- границя добутку функцій дорівнює

- границя частки функцій дорівнює

5. Як розкрити невизначеність виду при розв^/ язуванні границі:

6. Як розкрити невизначеність виду при розв^/ язуванні границі:

7. Як розв^/ язуються ірраціональні границі:

8. Запишіть - першу чудову границю

- другу чудову границю

9. Запишіть основні формули скороченого множення a² - b² = a³ - b³ = a³ + b³ = (a + b)² = (a - b)² = (a + b)³ = (a - b)³ =

10. Запишіть формули розкладання квадратного тричлена на лінійні множники:

1. ax² + bx + c =

D =

Корені повного квадратного рівняння знаходять за формулами: