Практичне заняття № 1

Тема заняття: Розв`язування систем лінійних рівнянь

Мета заняття: Вдосконалити навички розв’язування СЛАР за формулами Крамера і методом Гауса.

Література

№	Назва підручника	Автори	Сторінки до теми
1	Математика	В.М.Лейфура, Г.І. Городницький, Й.Й.Файст	с. 272-281, 291-297
2	Математика	В.Т.Лисичкин, И.Л. Соловейчик	с. 71-80
3	Математика для техникумов	И.И. Валуцэ, Г.Д. Дилигул

Основні формули та алгоритми:

1. З апишіть формулу обчислення визначника другого порядку:

2. Запишіть формулу обчислення визначника третього порядку:

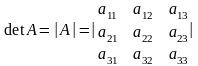
3. Записати алгоритм розв^/язування СЛАР методом Крамера:

4. Запишіть алгоритм розв^/язування СЛАР методом Гауса:

Роздатковий матеріал №1

1. Обчислити визначники:

а)

б)

в)

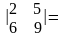
2. Розв’язати системи за правилом Крамера:

а) б)

3. Розв’язати системи методом Гауса:

а) б)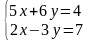

4.Обчислити визначники

а)

б)

в)

Розв’язати системи за правилом Крамера та методом Гауса:

11. 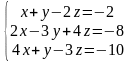12. 13.

Домашня робота: Лекція №1

Обчислити 1.

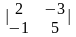
2.

3.

Розв’язати СЛАР за правилом Крамера та методом Гаусса:

4. 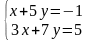5.

Практичне заняття №2

Тема заняття: Розв’язування задач на пряму лінію на площині і в просторі.

Мета заняття: вдосконалити застосування формул задання прямої на площині та вміти знаходити рівняння прямої, яка паралельна або перпендикулярна до даної.

Література

№	Назва підручника	Автори	Сторінки до теми
1	Математика	В.М.Лейфура, Г.І. Городницький, Й.Й.Файст	с. 113-128
2	Математика	В.Т.Лисичкин, И.Л. Соловейчик	с. 141-151
3	Математика для техникумов	И.И. Валуцэ, Г.Д. Дилигул	с. 119-143

Основні формули та алгоритми.

1. Загальне рівняння прямої має вид:

2. Щоб побудувати пряму треба:

3. Рівняння прямої, що проходить через дві точки має вид:

4. Запишіть рівняння прямої, що проходить через точку і має кутовий коефіцієнт:

5. Запишіть умову паралельності прямих:

6. Запишіть умову перпендикулярності прямих:

7. Запишіть косинус кута між прямими:

8. Запишіть формулу відстані від даної точки до прямої:

9. Запишіть рівняння прямої у відрізках:

Роздатковий матеріал №2

ЗАВДАННЯ 1. Пряму задано рівнянням 3х- 5у + 15 = 0.

а) перевірити, які з точок А (- 2, 3), В (0, 3), С (5, 6) належать заданій прямій;

б) знайти її рівняння з кутовим коефіцієнтом;

в) знайти її рівняння у відрізках на осях та побудувати її.

ЗАВДАННЯ 2. Побудувати прямі х+4=0; у-3=0, 3х-4у+12=0.

ЗАВДАННЯ 3. Знайти рівняння сторін трикутника, вершини якого А(1;-1), В(3;5), С(-7;11).

ЗАВДАННЯ 4. Знайти рівняння прямої, що проходить через точку М(2;5), паралельно прямій 3х-4у+15=0.

ЗАВДАННЯ 5. Знайти рівняння прямої, що проходить через точку К(5;-1) і перпендикулярна до прямої 3х-7у+14=0

ЗАВДАННЯ 6. Задано вершини трикутника АВС А(7; -3); В(-1; 6); С(3; 5).

Знайти: а) рівняння сторони ВС трикутника; б) рівняння медіани ВМ;

с) рівняння висоти АD і її довжину.

Домашня робота

Завдання 1. Загальне рівняння прямої 2х-3у+6=0 представити у вигляді

а) з кутовим коефіцієнтом;

б) у відрізках на осях;

в) побудувати пряму;

г) записати рівняння прямих паралельної та перпендикулярної до даної, які проходять через т.М (-1;3).

Завдання 2. Задано вершини трикутника АВС А(4;-2), В(-3;0), С(-6;-5)

Знайти: а) рівняння сторони ВС трикутника; б) рівняння медіани ВМ;

с) рівняння висоти АD і її довжину.

Практичне заняття №3

Тема заняття: Розв’язування задач на криві лінії другого порядку на площині.

Мета заняття: Навчити розв’язувати задачі на лінії другого порядку та вміти визначати тип кривої за даним рівнянням.

Література

№	Назва підручника	Автори	Сторінки до теми
1	Математика	В.М.Лейфура, Г.І. Городницький, Й.Й.Файст	c.133-155
2	Математика	В.Т.Лисичкин, И.Л. Соловейчик	c.152-160
3	Математика для техникумов	И.И. Валуцэ, Г.Д. Дилигул	c.145-170