5. Расчёт фермы
Расчёт усилий в стержнях фермы проводится либо графоаналитическим методом Максвелла-Кремоны, либо аналитическим методом, по выбору студента.
В первом случае строятся две диаграммы Максвелла-Кремоны, отдельно для постоянной и снеговой нагрузки и отдельно от тельферной нагрузки, причём в обоих случаях нагрузка прикладывается только к одной половине фермы. Так как постоянная нагрузка не меняет своего положения, рассматриваются рассматриваются следующие сочетания нагрузок: снег на левой половине -тельфер на левой половине; снег на правой половине -тельфер на левой половине; снег на левой половине -тельфер на правой половине; снег на правой половине -тельфер на правой половине. Это делается из-за того, что усилия в некоторых раскосах и стойках могут поменять знак. Усилия в поясах при любых сочетаниях нагрузок знак не меняют. Так усилия в стержнях верхнего пояса всегда имеют знак "минус" (сжатие), а усилия в стержнях нижнего пояса всегда иеют знак "плюс" (растяжение).
При выборе аналитического метода, расчёт усилий производится от полной нагрузки (постоянная + снеговая + тельферная). Учитывая симметрию самой фермы и нагрузки, расчёт проводится только для половиныфермы.
5.1. Расчёт усилий в стержнях фермы графоаналитическим
методом Максвелла-Кремоны
5.1.1 Правило построения диаграммы Максвелла-Кремоны для постоянной иснеговой нагрузок.
Вычерчиваем схему заданной фермы в масштабе с учётом всех уклонов и заданных размеров. При этом, следует учесть, что фактический пролёт фермы несколько отличается от заднного L. Фактический пролёт Lфакт = L∙cos γ, или, в нашем случае,
Lфакт = 16∙cos 7,125° =15,876 м
где угол ската γ= arc tg i = arc tg 1/8 = 7,125°
Прикладываем к узлам половины верхнего пояса единичные узловые нагрузки, как показано на рис.3. На крайний и центральный узлы - 0,5, на промежуточные - 1,0. Также прикладываем опорные реакции.
Определяем опорые реакции из условий равновесия.
Сумма моментов сил относительно левой опоры должна равнятьс нулю, т.е.
1∙d∙ cos γ + 1∙2d∙ cos γ + 1∙3d∙ cos γ + 0,5∙d∙4 cos γ -В∙8d∙ cos γ = 0, или, после сокращения,
8 = 8В, откуда В=1.
Здесь: d - длина панели верхнего пояса.
Сумма проекций всех сил на вертикальную ось должна равняться нулю, т.е.
А-0,5 -1-1-1-0,5 +В = 0, или А-4+В = 0, откуда А = 4-В = 4 -1 = 3
Обозначим внешние области буквами а, б, в, г, д, е и ж. Внешние области - это области с внешней стороны фермы, расположенные между силами (силы - это единичные узловые нагрузки и опорные реакции). Внутренние области обозначим цифрами, как показано на рис.3.
Назначаем масштаб сил. Так как построения велись в AutoCad, принято 1 = 2000 мм.
При общем масштабе схемы фермы М 1:100, масштаб сил на листе формата А4, 1 = 20 мм
Проводим с правой стороны листа вертикальную прямую и отметим на ней точку "а".
Чтобы перейти из области "а" в область "б", надо "перескочить" через единичную силу 0,5 по напрвлению этой силы, т.е. из т. "а" опуститься на 0,5 = 10 мм. На вертикальной прямой получим т. "б".
Аналогично, чтобы перейти из области "б" в область "в", надо "перескочить" через единичную силу 1,0 по направлению этой силы, т.е. из т. "б" опуститься на 1,0 = 20 мм. На вертикальной прямой получим т. "в".
Аналогично, чтобы перейти из области "в" в область "г", надо "перескочить" через единичную силу 1,0 по направлению этой силы, т.е. из т. "в" опуститься на 1,0 = 20 мм. На вертикальной прямой получим т. "г".
Аналогично, чтобы перейти из области "г" в область "д", надо "перескочить" через единичную силу 1,0 по направлению этой силы, т.е. из т. "г" опуститься на 1,0 = 20 мм. На вертикальной прямой получим т. "д".
Аналогично, чтобы перейти из области "д" в область "е", надо "перескочить" через единичную силу 0,5 по направлению этой силы, т.е. из т. "д" опуститься на 0,5 = 10 мм. На вертикальной прямой получим т. "е".
Аналогично, чтобы перейти из области "е" в область "ж", надо "перескочить" через реакцию В = 1,0 по направлению этой силы, т.е. из т. "е" подняться на 1,0 = 20 мм. На вертикальной прямой получим т. "ж".
Чтобы перейти из области "ж" в область "а", надо "перескочить" через реакцию А = 3,0 по направлению этой силы, т.е. из т. "ж" подняться на 3,0 = 60 мм. На вертикальной прямой получим т. "а", т.е. вернёмся в самое начало.
Через полученные точки на вертикальной прямой проводим прямые, параллельные одноимённым областям. Так из точек "б", "в", "г" и "д" проводим прямые, параллельные левому скату. Из точки "е" проводим прямую, параллельную правому скату.
Из точки "ж" проводим горизонтальную прямую, параллельную нижнему поясу.
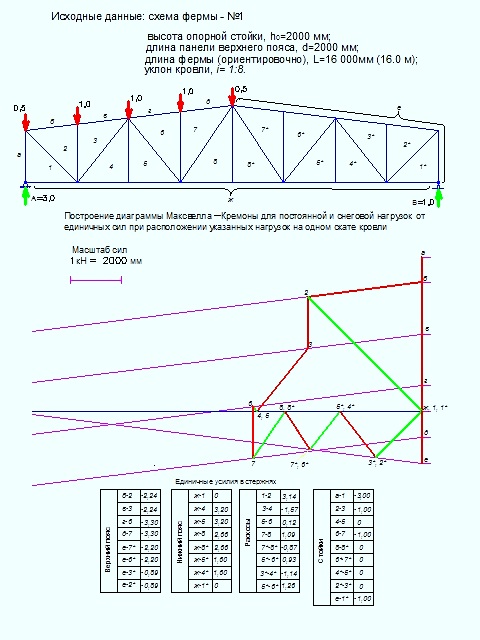
Рис.3
Усилие в стержне "а-1" (здесь и далее, обозначение стержня содержит маркировки областей по обе стороны стержня) направлено по вертикали. Область "1" граничит с
областью "ж".
Поэтому точка "1" находится одновременно и на вертикальной прямой и на горизонтальной прямой, т.е. совпадает с точкой "ж". Усилие в стержне "а-1" соответствует отрезку "а-1" на вертикальной прямой.
Для построения отрезка "1-2" из уже построенной точки "1" проводим прямую, параллельную стержню "1-2" до пересечения с прямой, проходящей через т. "б" , так как область "2" граничит с областью "б". Полученная точка пересечения - точка "2".
Усилие в стержне "1-2" соответствует отрезку "1-2" на диаграмме. Усилие в стержне
"б-2" соответствует отрезку "б-2" на диаграмме.
Строим на диаграмме отрезок "2-3". Точка "2" уже построена. Область "2" граничит с областью "б", в то же время область "3" граничит с областью "в". Усилие в стержне "2-3" направлено по вертикали, поэтому точку "3" строим, опустив перпендикуляр из т. "2" до пересечения с наклонной прямой, проходящей через т. "в". Усилие в стержне "2-3" соответствует отрезку "2-3" на диаграмме. Отрезок "в-3" соответствует усилию в одноимённом стержне.
Строим на диаграмме отрезок "3-4". Точка "3" уже построена. Область "3" граничит с областью "в", в то же время область "4" граничит с областью "ж". Усилие в стержне "3-4" направлено вдоль стержня "3-4", поэтому точку "4" строим, проведя из т. "3" прямую, параллельную стержню"3-4" до пересечения с горзонтальной прямой, проходящей через
точку "ж". Усилие в стержне "3-4" соответствует отрезку "3-4" на диаграмме. Отрезок
"ж-4" соответствует усилию в одноимённом стержне нижнего пояса.
Строим отрезок "4-5" соответствующий усилию в одноимённом стержне. . Область "4" и область "5" граничат одновременно с областью "ж", поэтому точки "4" и "5" совпадают. Поэтому и отрезок "4-5" и, соответственно, усилие в стержне "4-5" равны нулю. Отрезок
"ж-5" соответствует усилию в одноимённом стержне нижнего пояса.
Строим на диаграмме отрезок "5-6". Точка "5" уже построена. Область "5" граничит с областью "ж", в то же время область "6" граничит с областью "г". Усилие в стержне "5-6" направлено вдоль стержня "5-6", поэтому точку "6" строим, проведя из т. "5" прямую, параллельную стержню"5-6" до пересечения с наклонной прямой, проходящей через
точку "г". Усилие в стержне "5-6" соответствует отрезку "5-6" на диаграмме. Отрезок
"г-6" соответствует усилию в одноимённом стержне верхнего пояса.
Строим на диаграмме отрезок "6-7". Точка "6" уже построена. Область "6" граничит с областью "г", в то же время область "7" граничит с областью "д". Усилие в стержне "6-7" направлено по вертикали, поэтому точку "7" строим, опустив перпендикуляр из т. "6" до пересечения с наклонной прямой, проходящей через т. "д". Усилие в стержне "6-7" соответствует отрезку "6-7" на диаграмме. Отрезок "д-7" соответствует усилию в одноимённом стержне верхнего пояса.
Строим на диаграмме отрезок "7-8". Точка "7" уже построена. Область "7" граничит с областью "д", в то же время область "8" граничит с областью "ж". Усилие в стержне "7-8" направлено вдоль стержня "7-8", поэтому точку "8" строим, проведя из т. "7" прямую, параллельную стержню"7-8" до пересечения с горзонтальной прямой, проходящей через
точку "ж". Усилие в стержне "7-8" соответствует отрезку "7-8" на диаграмме. Отрезок
"ж-8" соответствует усилию в одноимённом стержне нижнего пояса.
Строим отрезок "8-8*" соответствующий усилию в одноимённом стержне. . Область "8" и область "8*" граничат одновременно с областью "ж", поэтому точки "8" и "8*" совпадают. Поэтому и отрезок "8-8*" и, соответственно, усилие в стержне "8-8*" равны нулю. Отрезок "ж-8*" соответствует усилию в одноимённом стержне нижнего пояса.
Строим на диаграмме отрезок "7*-8*". Точка "8*" уже построена. Область "8*" граничит с областью "ж", в то же время область "7*" граничит с областью "е". Усилие в стержне "7*-8*" направлено вдоль стержня"7*-8*", поэтому точку "7*" строим, проведя
из т. "8*" прямую, параллельную стержню"7*-8*" до пересечения с наклонной прямой, проходящей через т. "е". Усилие в стержне "7*-8*" соответствует отрезку "7*-8*" на диаграмме. Отрезок "е-7*" соответствует усилию в одноимённом стержне верхнего пояса.
Строим отрезок "6*-7*" соответствующий усилию в одноимённом стержне. . Область "6*" и область "7*" граничат одновременно с областью "е", поэтому точки "6*" и "7*" совпадают. Поэтому и отрезок "6*-7*" и, соответственно, усилие в стержне "6*-7*" равны нулю. Отрезок
"е-6*" соответствует усилию в одноимённом стержне верхнего пояса.
Строим на диаграмме отрезок "5*-6*". Точка "6*" уже построена. Область "5*" граничит с областью "ж", в то же время область "6*" граничит с областью "е". Усилие в стержне "5*-6*" направлено вдоль стержня"5*-6*", поэтому точку "5*" строим, проведя
из т. "6*" прямую, параллельную стержню"5*-6*" до пересечения с горизонтальной прямой, проходящей через т. "ж". Усилие в стержне "5*-6*" соответствует отрезку "5*-6*" на диаграмме. Отрезок "ж-5*" соответствует усилию в одноимённом стержне нижнего пояса.
Строим отрезок "4*-5*" соответствующий усилию в одноимённом стержне. . Область "4*" и область "5*" граничат одновременно с областью "ж", поэтому точки "4*" и "5*" совпадают. Поэтому и отрезок "4*-5*" и, соответственно, усилие в стержне "4*-5*" равны нулю. Отрезок "ж-4*" соответствует усилию в одноимённом стержне нижнего пояса.
Строим на диаграмме отрезок "3*-4*". Точка "4*" уже построена. Область "4*" граничит с областью "ж", в то же время область "3*" граничит с областью "е". Усилие в стержне "3*-4*" направлено вдоль стержня"3*-4*", поэтому точку "3*" строим, проведя
из т. "4*" прямую, параллельную стержню"3*-4*" до пересечения с наклонной прямой, проходящей через т. "е". Усилие в стержне "3*-4*" соответствует отрезку "3*-4*" на диаграмме. Отрезок "е-3*" соответствует усилию в одноимённом стержне верхнего пояса
Строим отрезок "2*-3*" соответствующий усилию в одноимённом стержне. . Область "3*" и область "2*" граничат одновременно с областью "е", поэтому точки "2*" и "3*" совпадают. Поэтому и отрезок "2*-3*" и, соответственно, усилие в стержне "2*-3*" равны нулю. Отрезок
"е-2*" соответствует усилию в одноимённом стержне верхнего пояса.
Строим на диаграмме отрезок "1*-2*". Точка "2*" уже построена. Область "1*" граничит с областью "ж", в то же время область "2*" граничит с областью "е". Усилие в стержне "1*-2*" направлено вдоль стержня"1*-2*", поэтому точку "1*" строим, проведя
из т. "2*" прямую, параллельную стержню"1*-2*" до пересечения с горизонтальной прямой, проходящей через т. "ж". Усилие в стержне "1*-2*" соответствует отрезку "1*-2*" на диаграмме. Отрезок "ж-1*" равен нулю и соответствует усилию в одноимённом стержне нижнего пояса.
Единичные усилия в каждом стержне получаем, измерив длину соответствующего отрезка и разделив её на длину отрезка масштаба сил.
Правило знаков:
Выбирается узел, в который приходит интересующий нас стержень. Считая узел центром вращения, обходим наш стержень по часовой стрелке, например, для стержня "2-1" мы из области "2" переходим в область "1" и смотрим на диаграмме куда мы движемся, идя от точки "2" к точке "1". В данном случае мы движемся от узла, т.е. растягиваем стержень. Соответственно усилие имеет знак "плюс".
Другой пример. Рассмотрим стержень "2-3",находясь в нижнем узле. Обходя этот стержень по часовой стрелке, мы из области "2" переходим в область "3". На диаграмме, идя от точки"2" в точку "3" мы движемся по направлению к узлу, т.е. сжимаем стержень. В этом случае усилие имеет знак "минус".
Плученные значения единичных усилий с учётом знака заносим в таблички на рис.3