В) Описание операций
Операции определяют содержимое базы знаний модели. Объект операций имеет следующий формат:
$Operations
<описание операции> {<описание операции>}
$End
Описание каждой операции имеет следующий формат:
<имя операции>: <имя образца> <значения параметров образца>
Г) Объект описания показателей
Показатели, которые требуется собрать в процессе прогона модели, описываются в отдельном объекте следующего формата:
$Results
<описание показателя> {<описание показателя>}
$End
В свою очередь описание отдельного показателя имеет формат:
<имя показателя>: [trace | no trace] <вид показателя> <описатель>
Виды собираемых показателей с соответствующими описателями:
watch par <имя параметра ресурса> - наблюдать значение параметра ресурса;
watch state <логическое выражение> - наблюдать состояние системы;
watch_quant <имя типа> [NoCheck | <логическое выражение>] - наблюдать количество временных ресурсов;
watch_value <имя типа> [NoCheck | <логическое выражение>] <арифметическое выражение> - наблюдать значение параметра временного ресурса в момент уничтожения ресурса;
get value <арифметическое выражение> - наблюдать значение в момент окончания прогона.
3.5 Поиск решений в продукционных системах а) Введение
Для решения задачи поиска необходимо определить:
глобальную базу данных (ГБД);
набор правил преобразования;
задать стратегию управления, где глобальная БД описывает состояние системы, набор правил преобразования определяет законы изменения ГБД, а стратегия управления определяет каким образом применять правила преобразования.
В языке имитационного моделирования РДО эти компоненты могут быть соответственно представлены в объектах:
типов ресурсов и ресурсов (RTP и RSS);
образцов операций (PAT);
точек принятия решения (DPT).
В качестве примера, будем решать задачу расстановки фишек в игре в 8 (Рис.17).
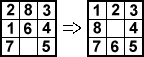
Рис.17. Пример игры в восемь
Множество возможных состояний системы (ГБД) называется пространством состояний (Рис.18). В реальных задачах пространство состояний велико, в этой игре оно равно (3*3)! = 362880. Доказано, что оно распадается на два подпространства, причем из одного нельзя попасть в другое начальными ходами. В нашем случае: 2*181440.
Рис.18. Схема пространства состояний
Решение задачи поиска на графе сводится к нахождению пути от исходной к целевой вершине. При этом на путь могут быть наложены ограничения, например, путь не должен проходить через определенные вершины.
Б) Основная процедура поиска
DATA = (ГБД) - исходное состояние
Until DATA <удовлетворяет терминальному условию> do
begin
Select <некоторое правило П из тех, которые можно применить к DATA>
DATA = П(DATA) - применяем правило П к DATA и формируем новый DATA
end
Алгоритм процедуры прост - на первом шаге мы задаем начальное состояние системы, например, расстановку фишек. Далее, в цикле мы применяем возможные правила к DATA, меняя тем самым состояние системы, до тех пор, пока не достигнем целевой вершины, т.е. пока не удовлетворим терминальное условие поиска.
Самым ответственным моментом является способ выбора правила на шаге 4, т.к. от него зависит стратегия управления (Рис.19).
Рис.19. Выбор правила
Существуют две стратегии управления:
1. безвозвратная - не можем вернуться при неудачном ходе;
2. пробная:
стратегия с возвращением - запоминается текущий путь к точке возврата (там, где было разветвление), но помниться только один путь;
поиск на графе - запоминает все пути, а не один, но большие затраты по ресурсам.
Далее будем рассматривать поиск на графе, т.к. именно он реализован в РДО-имитаторе и РДО-языке.
Эта стратегия запоминает все исследуемые пути. Они сохраняются в графе, вершинами которого являются состояния системы, а дугами – продукционные правила. Это неявно заданный граф, т.к. он задан начальной вершиной и правилами построения. При этом решается задача – найти путь между заданной (начальной) и целевой вершинами.
Достоинство: можно найти оптимальное решение.
Недостаток: метод сложен из-за большой размерности графа.
Рассмотрим эту стратегию поподробнее.
В результате работы поиска мы получаем направленный граф (Рис.20).
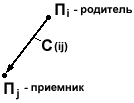
Рис.20. Граф поиска
S - корень графа, имеет глубину, равную нулю.
При применении правила к вершине родителя, порождается вершина-потомок (приемник). Путь – последовательность вершин, в котором каждая последующая является приемником. Стоимость применения правила соответствует стоимости дуги (С) между родителем и приемником.
Таким образом, стоимость пути к вершине равняется сумме стоимости правил, примененных для ее достижения.
Процесс применения всех возможных правил, т.е. получение всех возможных приемников, называется раскрытием.
Рассмотрим общую процедуру поиска на графе (Рис.21).
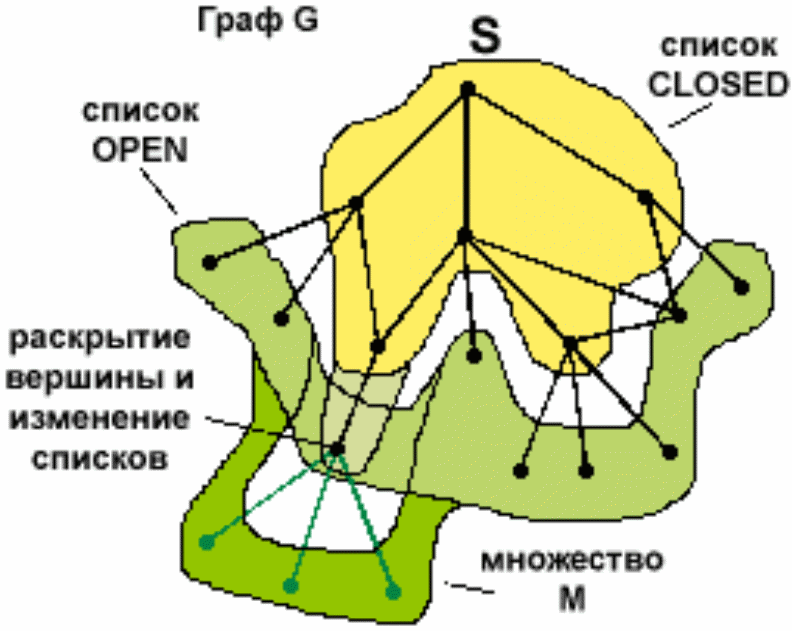
Рис.21. Общая процедура поиска на графе
Создать граф поиска G, состоящий из вершины S, и создать список OPEN, который содержит вершину S
Создать список CLOSED, который пуст
Loop{если OPEN пуст, то неудача
Выбрать первую вершину в OPEN, убрать ее из OPEN и переместить в CLOSED, назвав ее n
Если n - целевая вершина, то решение найдено, успех
Раскрыть вершину n, порождая множество M ее приемников, не являющихся предками, добавить в G
Ввести указатель к n от тех элементов из M, которых еще в графе нет, добавить эти элементы в OPEN. Для каждого элемента из M, который уже есть в OPEN или CLOSED (вместе это граф G), решить, нужно ли переориентировать указатель на n (если путь через новую вершину n короче, то необходимо поменять родителей (Рис.22). Для каждого элемента из M, который находится в CLOSED, принять решение относительно ее потомка и так до полной перестройки графа.
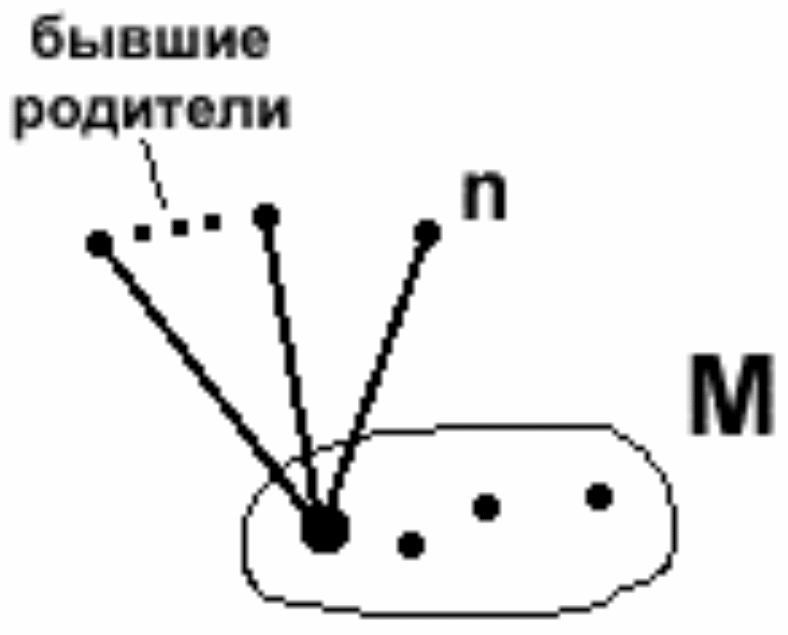
Рис.22. Смена родителя
Переупорядочить список OPEN в соответствии с некоторой процедурой (выбираем новую перспективную вершину)
перейти к метке Loop
Этот алгоритм порождает явно граф G, который является подграфом графа состояний задачи и содержит в себе дерево поиска T (все удачные вершины).
Если граф G – дерево, то каждая новая вершина ни с кем не совпадает. Поэтому вершины упорядочиваются в сбалансированное бинарное дерево. Можно достичь тех же результатов и без использования структуры дерева, но это потребует больших ресурсов вычислительной техники, т.к. будут раскрываться все вершины до конца со своими потомками.
Рассмотрим пример смены родителя (Рис.23)
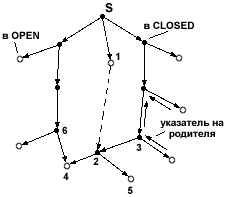
Рис.23. Пример смены родителя
Именно по связям с родителем и строится дерево поиска T (по длине пути). Предположим, что каждая дуга графа имеет вес, равный единице и связь вершины 4 с вершиной S через вершину 2 отсутствует, т.к. длина через нее больше 4 (длина равна 4 через вершину 6). В данный момент времени раскрывается вершина 1, и порождается единственный приемник, совпадающий с вершиной 2. Теперь вершина 2 связана с S путем = 2, а не 4. Так же пересматриваются приемники вершины 2. Выясняется, что вершина 4 теперь имеет до S путь = 3, а вершина 5 - путь = 3. В результате чего, родителем вершины 4 назначается вершина 2 (для вершины 5 все так и остается, потому что она имела только одного родителя).
в) Применение оценочной функции
Вернемся к алгоритму общей процедуры поиска на графе, а именно к шагу 8. На нем принимается решение по выбору следующей раскрываемой вершины, т.к. оценочная функция упорядочивает по возрастанию все вершины в списке OPEN, а первая из итого списка и будет обработана на шаге 4 алгоритма. Таким образом, выбор оценочной функции существенно влияет на количество раскрываемых вершин, т.к. позволяет не обрабатывать заведомо невыгодные вершины.
Рассмотрим две основные не информируемые процедуры поиска (два крайних случая):
поиск в глубину;
поиск в ширину.