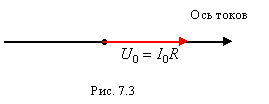- •Содержание
- •7.1.Переменный ток
- •1. Электростатика. Электрическое поле в вакууме
- •1.1. Электрические заряды и их взаимодействие
- •1.2. Электризация тел
- •1.3. Закон Кулона. Системы единиц
- •1.4. Близкодействие и действие на расстоянии. Электрическое поле
- •1.5. Напряженность электрического поля
- •1.6. Электрическое поле диполя
- •1.7. Теорема Гаусса
- •1.8. Потенциал электрического поля
- •1.9. Эквипотенциальные поверхности
- •1.10. Связь между напряженностью и разностью потенциалов
- •2. Электрическое поле в веществе
- •2.1. Проводники в электростатическом поле
- •2.2. Проводники во внешнем электрическом поле
- •2.3. Емкость проводников
- •2.4. Конденсаторы. Емкость конденсаторов
- •2.5. Соединение конденсаторов
- •2.6. Энергия плоского конденсатора
- •2.7. Диэлектрики в электростатическом поле
- •2.8. Молекулярная картина поляризации диэлектриков
- •2.9. Влияние поляризации на электрическое поле
- •3. Постоянный электрический ток
- •3.1. Постоянный электрический ток. Сила тока. Плотность тока
- •3.2. Электродвижущая сила
- •3.3. Закон Ома
- •3.4. Правила Кирхгофа
- •3.5 Последовательное и параллельное соединение проводников
- •3.6 Последовательное и параллельное соединение источников тока
- •3.7. Закон Джоуля–Ленца
- •4. Магнитное поле в вакууме
- •4.1. Магнитное поле
- •4.2. Закон Био–Савара
- •4.3. Теорема о циркуляции
- •4.4. Сила Ампера
- •4.5. Сила Лоренца
- •4.6. Контур с током в магнитном поле
- •4.7. Теорема Гаусса для магнитных полей
- •4.8. Механическая работа в магнитном поле
- •5. Магнитное поле в веществе
- •5.1. Магнитная проницаемость
- •5.2. Виды магнетиков
- •6. Электромагнитная индукция
- •6.1. Явление электромагнитной индукции
- •6.2. Универсальный закон электромагнитной индукции
- •6.3 Явление самоиндукции
- •6.4. Энергия магнитного поля
- •6.5. Взаимная индукция
- •6.6. Примеры на применение явления электромагнитной индукции
- •7. Переменный ток
- •7.1. Переменный ток
- •7.2. Квазистационарные токи
- •7.3. Сопротивление в цепи переменного тока
- •7.4. Индуктивность в цепи переменного тока
- •7.5. Цепь с емкостью
- •7.6. Цепь переменного тока, содержащая активное сопротивление, индуктивность и емкость
- •7.7. Работа и мощность переменного тока
- •7.8. Эффективные значения тока и напряжения
- •7.9. Резонансы в цепи переменного тока
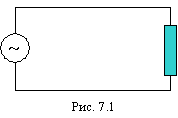
7.3. Сопротивление в цепи переменного тока
|
|
|
|
|
|
|
||
|
|
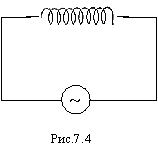
7.4. Индуктивность в цепи переменного тока
|
|
|
|
В рассматриваемом случае
![]() ,
а
,
а
![]() .
Приложенное напряжение в точности
уравновешивается электродвижущей силой
самоиндукции. Если сила тока в цепи
,
то падение напряжения на индуктивности
равно
.
Приложенное напряжение в точности
уравновешивается электродвижущей силой
самоиндукции. Если сила тока в цепи
,
то падение напряжения на индуктивности
равно
![]() ,
где
,
где
![]() .
.
|
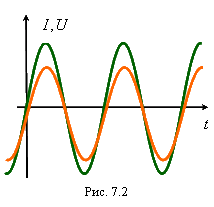
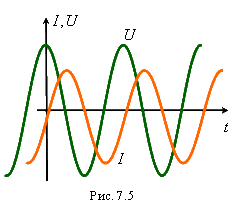
Физическая причина возникновения
разности фаз между током и напряжением
на индуктивности заключается в следующем.
При нарастании тока в катушке индуктивности
возникает индукционный ток, который в
этом случае будет направлен, согласно
правилу Ленца, навстречу основному
току. Поэтому изменение тока будет
отставать по фазе от изменения напряжения.
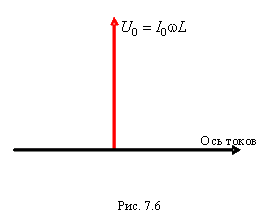
Сравнивая выражение для
![]() c
законом Ома, можно видеть, что величина
c
законом Ома, можно видеть, что величина
![]() играет
роль сопротивления. Его принято называть
индуктивным сопротивлением. Индуктивное
сопротивление зависит от частоты,
поэтому при больших частотах даже малые
индуктивности могут представлять
большие сопротивления для переменных
токов. Для постоянного тока индуктивность
не является сопротивлением.
играет
роль сопротивления. Его принято называть
индуктивным сопротивлением. Индуктивное
сопротивление зависит от частоты,
поэтому при больших частотах даже малые
индуктивности могут представлять
большие сопротивления для переменных
токов. Для постоянного тока индуктивность
не является сопротивлением.
|
Индуктивное сопротивление используется для устройства дросселей, представляющих собой проволочные катушки, вводимые в цепь переменного тока. Введение дросселей позволяет регулировать силу тока, при этом не происходит дополнительных потерь энергии, связанных с выделением тепла согласно закону Джоуля–Ленца.
Пояснение
Если использование элементов высшей математики при изучении этого параграфа вызывает затруднения, можно использовать представления о малых приращениях переменных величин
В рассматриваемом случае
![]() ,
а
,
а
![]() .
Приложенное напряжение в точности
уравновешивается электродвижущей силы
самоиндукции. Если сила тока в цепи
,
то падение напряжения на индуктивности
равно
.
Приложенное напряжение в точности
уравновешивается электродвижущей силы
самоиндукции. Если сила тока в цепи
,
то падение напряжения на индуктивности
равно
![]() .
Изменение силы тока за малый интервал
времени
равно
.
Изменение силы тока за малый интервал
времени
равно
![]() .
.
Так как время
мало,
то
![]() ,
,
![]() ,
следовательно,
,
следовательно,
![]() .
Отсюда получаем, что
.
Отсюда получаем, что
![]() .
Напряжение на индуктивности будет равно
.
Напряжение на индуктивности будет равно
![]() .
.
Таким образом, приходим к тому же результату: напряжение на индуктивности изменяется по периодическому закону с амплитудой , но колебания напряжения на индуктивности опережают колебания тока на .