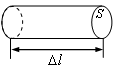
4.5. Сила Лоренца

Рис. 4.12

Так как электрический ток представляет направленное движение заряженных частиц, то, зная силу, действующую на проводник с током, можно определить силу, действующую со стороны магнитного поля на движущийся заряд. Выделим элемент проводника длиной  и поперечным сечением S (рис. 4.12). При силе тока I в единицу времени через сечение проводника пройдут все заряды, которые находятся на расстоянии, равном скорости движения зарядов, от данного сечения. Следовательно, по определению силы тока , где n – концентрация частиц.

Сила, действующая на элемент тока длиной , равна . Эта сила представляет собой сумму сил, действующих на все  зарядов в выделенном элементе проводника. В рассматриваемом случае все эти силы параллельны друг другу, поэтому сила, действующая на один заряд, будет равна

,

где a – угол между направлением скорости заряда  и вектором магнитной индукции . Эта сила называется магнитной составляющей силы Лоренца. Если вектор  перпендикулярен , то магнитная составляющая силы Лоренца равна

.

Направление силы Лоренца определяется для положительных зарядов по правилу левой руки: если магнитные силовые линии входят в ладонь, а четыре выпрямленных пальца показывают направление скорости заряженной частицы, то отогнутый большой палец показывает направление силы Лоренца, действующей на заряд.

Сила Лоренца всегда перпендикулярна к скорости, поэтому работы не совершает, а это означает, что в постоянном магнитном поле энергия движущейся частицы остается неизменной.

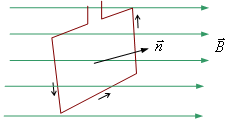
4.6. Контур с током в магнитном поле

Рис. 4.13

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором  и нормалью к площади :

.

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

.

Это выражение также можно использовать для определения индукции магнитного поля:

.

Величину, равную произведению , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

.

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

4.7. Теорема Гаусса для магнитных полей

Подобно тому, как было введено понятие потока вектора напряженности электрического поля, введем понятие потока вектора магнитной индукции, или магнитного потока. Элементарный магнитный поток  через малую элементарную площадку , которую можно считать плоской, и в окрестности которой магнитное поле можно считать однородным, равен произведению вектора индукции на площадь выделенного элемента поверхности и косинус угла между вектором индукции и нормалью к поверхности:

.

Поток может быть как положительным, так и отрицательным в зависимости от направления нормали к поверхности.

За единицу магнитного потока в системе единиц СИ принят вебер (Вб). 1 Вб – это магнитный поток через поверхность площадью , расположенную в однородном магнитном поле перпендикулярно вектору индукции , равному по модулю :

.

В случае неоднородного магнитного поля поток через какую-либо поверхность равен алгебраической сумме потоков через участки поверхности, вблизи которых поле можно считать однородным.

Магнитный поток, как и поток вектора напряженности электрического поля, можно считать равным числу магнитных силовых линий, пересекающих рассматриваемую поверхность. Магнитное поле является вихревым, то есть его линии магнитной индукции замкнуты. Поэтому замкнутая поверхность, помещенная в магнитное поле, пронизывается линиями магнитной индукции так, что любая линия, входящая в эту поверхность, выходит из нее. Следовательно, полный магнитный поток через произвольную замкнутую поверхность равен нулю. Это утверждение носит название теоремы Гаусса для магнитных полей. Равенство нулю магнитного потока через замкнутую поверхность является следствием того, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами.