- •Содержание
- •7.1.Переменный ток
- •1. Электростатика. Электрическое поле в вакууме
- •1.1. Электрические заряды и их взаимодействие
- •1.2. Электризация тел
- •1.3. Закон Кулона. Системы единиц
- •1.4. Близкодействие и действие на расстоянии. Электрическое поле
- •1.5. Напряженность электрического поля
- •1.6. Электрическое поле диполя
- •1.7. Теорема Гаусса
- •1.8. Потенциал электрического поля
- •1.9. Эквипотенциальные поверхности
- •1.10. Связь между напряженностью и разностью потенциалов
- •2. Электрическое поле в веществе
- •2.1. Проводники в электростатическом поле
- •2.2. Проводники во внешнем электрическом поле
- •2.3. Емкость проводников
- •2.4. Конденсаторы. Емкость конденсаторов
- •2.5. Соединение конденсаторов
- •2.6. Энергия плоского конденсатора
- •2.7. Диэлектрики в электростатическом поле
- •2.8. Молекулярная картина поляризации диэлектриков
- •2.9. Влияние поляризации на электрическое поле
- •3. Постоянный электрический ток
- •3.1. Постоянный электрический ток. Сила тока. Плотность тока
- •3.2. Электродвижущая сила
- •3.3. Закон Ома
- •3.4. Правила Кирхгофа
- •3.5 Последовательное и параллельное соединение проводников
- •3.6 Последовательное и параллельное соединение источников тока
- •3.7. Закон Джоуля–Ленца
- •4. Магнитное поле в вакууме
- •4.1. Магнитное поле
- •4.2. Закон Био–Савара
- •4.3. Теорема о циркуляции
- •4.4. Сила Ампера
- •4.5. Сила Лоренца
- •4.6. Контур с током в магнитном поле
- •4.7. Теорема Гаусса для магнитных полей
- •4.8. Механическая работа в магнитном поле
- •5. Магнитное поле в веществе
- •5.1. Магнитная проницаемость
- •5.2. Виды магнетиков
- •6. Электромагнитная индукция
- •6.1. Явление электромагнитной индукции
- •6.2. Универсальный закон электромагнитной индукции
- •6.3 Явление самоиндукции
- •6.4. Энергия магнитного поля
- •6.5. Взаимная индукция
- •6.6. Примеры на применение явления электромагнитной индукции
- •7. Переменный ток
- •7.1. Переменный ток
- •7.2. Квазистационарные токи
- •7.3. Сопротивление в цепи переменного тока
- •7.4. Индуктивность в цепи переменного тока
- •7.5. Цепь с емкостью
- •7.6. Цепь переменного тока, содержащая активное сопротивление, индуктивность и емкость
- •7.7. Работа и мощность переменного тока
- •7.8. Эффективные значения тока и напряжения
- •7.9. Резонансы в цепи переменного тока
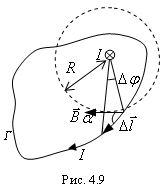
4.3. Теорема о циркуляции
|
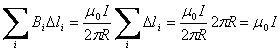 .
.
Из последнего соотношения видно, что циркуляция вектора магнитной индукции не зависит от радиуса контура.
В случае контура произвольной формы
![]() ,
но
,
но
![]() ,
где R – радиус окружности с центром
на проводнике с током, совпадающей на
малом участке с элементом контура
,
где R – радиус окружности с центром
на проводнике с током, совпадающей на
малом участке с элементом контура
![]() .
Так как вклад в циркуляцию от элемента
окружности любого радиуса одинаков, то
.
Так как вклад в циркуляцию от элемента
окружности любого радиуса одинаков, то
![]()
и
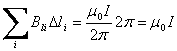 .
.
Таким образом, циркуляция вектора по произвольному контуру равна произведению m0 на силу тока I, пронизывающего контур, по которому берется циркуляция. Если контур не охватывает ток, то циркуляция вектора равна нулю.
Рис. 4.10 |
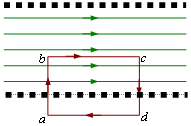
Пусть число витков соленоида на единицу
его длины равно n. Тогда полный ток,
который пронизывает контур, равен
![]() .
Согласно теореме о циркуляции
.
Согласно теореме о циркуляции
![]() ,
отсюда для бесконечно длинного соленоида
получим:
,
отсюда для бесконечно длинного соленоида
получим:
![]() .
.
Заметим, что вблизи краев соленоида поле уже не будет однородным, и его нельзя определить по полученной формуле. Кроме того, если соленоид нельзя считать бесконечно длинным, то индукция магнитного поля вне соленоида не равна нулю.
4.4. Сила Ампера
Магнитное поле, независимо от того,
создается оно проводником с током или
постоянным магнитом, проявляет себя в
том, что действует на проводник с током
или движущиеся заряды с некоторой силой.
Максимальное значение силы, действующей
на элемент проводника длиной
,
равно
![]() .
Оно достигается в том случае, когда угол
a между вектором
,
направление которого совпадает с
направлением тока, и вектором магнитной
индукции равен
.
Оно достигается в том случае, когда угол
a между вектором
,
направление которого совпадает с
направлением тока, и вектором магнитной
индукции равен
![]() .
При других значениях этого угла сила
.
При других значениях этого угла сила
![]() .
.
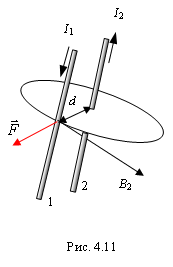
Эта сила называется силой Ампера. Направление силы Ампера определяется по правилу левой руки: если магнитные силовые линии входят в ладонь, а четыре выпрямленных пальца совпадают с направлением тока, то отогнутый большой палец указывает направление силы.
|
![]() ,
,
где d – расстояние между проводниками. Линии этого магнитного поля представляют собой концентрические окружности, перпендикулярные проводнику 1, поэтому сила Ампера
![]() .
.
Если рассмотреть силу, действующую на
элемент тока
![]() проводника
2, то получим такое же выражение. Используя
правило левой руки, легко показать, что
если токи текут в одном направлении, то
проводники притягиваются, если в
противоположных направлениях –
отталкиваются.
проводника
2, то получим такое же выражение. Используя
правило левой руки, легко показать, что
если токи текут в одном направлении, то
проводники притягиваются, если в
противоположных направлениях –
отталкиваются.
Закон взаимодействия токов используется для определения единицы силы тока в системе единиц СИ. По определению единица силы тока в системе единиц СИ – ампер – это сила постоянного тока, который, проходя по двум параллельным проводникам бесконечной длины и ничтожно малого сечения, расположенным в вакууме на расстоянии 1 м один от другого, создал бы между ними силу взаимодействия, равную 2 ? 10–7 Н на каждый метр длины. Отсюда получается значение магнитной постоянной m0:
![]() .
.