2.4. Типы сил

Все многообразие существующих в природе взаимодействий сводится к четырем типам: гравитационное, электромагнитное, сильное и слабое. Сильные и слабые взаимодействия существенны на столь малых расстояниях, когда законы механики Ньютона уже неприменимы. Все макроскопические явления в окружающем нас мире определяются гравитационным и электромагнитным взаимодействиями. Только для этих видов взаимодействий можно использовать понятие силы в смысле механики Ньютона. Гравитационные силы наиболее существенны при взаимодействии больших масс. Проявления электромагнитных сил чрезвычайно многообразны. Хорошо известные силы трения, упругие силы имеют электромагнитную природу. Поскольку второй закон Ньютона определяет ускорение тела независимо от природы сил, сообщающих ускорение, то в дальнейшем будем пользоваться так называемым феноменологическим подходом: опираясь на опыт, установим количественные закономерности для этих сил.

Упругие силы. Упругие силы возникают в теле, испытывающем воздействие других тел или полей, и связаны с деформацией тела. Деформации представляют собой особый вид движения, а именно перемещение частей тела относительно друг друга под действием внешней силы. При деформации тела изменяются его форма и объем. Для твердых тел различают два предельных случая деформации: упругие и пластические. Деформацию называют упругой, если она полностью исчезает после прекращения действия деформирующих сил. При пластических (неупругих) деформациях тела частично сохраняют измененную форму после снятия нагрузки.

Упругие деформации тел разнообразны. Под действием внешней силы тела могут растягиваться и сжиматься, изгибаться, скручиваться и т.д. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации. Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации.

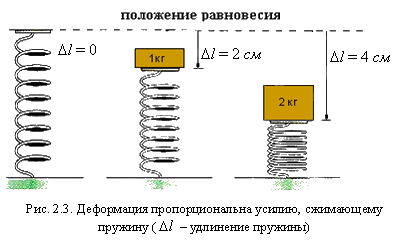
Опыт показывает, что при малых упругих деформациях величина деформации пропорциональна вызывающей ее силе (рис. 2.3). Это утверждение носит название закона Гука.

Роберт Гук (Robert Hooke), 1635–1702

Английский физик. Родился во Фрешуотере на острове Уайт в семье священника, окончил Оксфордский университет. Еще учась в университете, работал ассистентом в лаборатории Роберта Бойля, помогая последнему строить вакуумный насос для установки, на которой был открыт закон Бойля–Мариотта. Будучи современником Исаака Ньютона, вместе с ним активно участвовал в работе Королевского общества, а в 1677 г. занял там пост ученого секретаря. Как и многие другие ученые того времени, Роберт Гук интересовался самыми разными областями естественных наук и внес вклад в развитие многих из них. В своей монографии «Микрография» он опубликовал множество зарисовок микроскопического строения живых тканей и других биологических образцов и впервые ввел современное понятие «живая клетка». В геологии он первым осознал важность геологических пластов и первым в истории занялся научным изучением природных катаклизмов. Он же одним из первых высказал гипотезу, что сила гравитационного притяжения между телами убывает пропорционально квадрату расстояния между ними, и двое соотечественников и современников, Гук и Ньютон, так до конца жизни и оспаривали друг у друга право называться первооткрывателем закона всемирного тяготения. Гук разработал и собственноручно построил целый ряд важных научно-измерительных приборов. Он, в частности, первым предложил помещать перекрестье из двух тонких нитей в окуляр микроскопа, первым предложил принять температуру замерзания воды за ноль температурной шкалы, а также изобрел универсальный шарнир (карданное сочленение).

Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид:

,

где  – сила упругости;  – изменение длины (деформация) тела;  – коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ – ньютон на метр (Н/м). В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела. Сила упругости всегда направлена к положению равновесия. Сила упругости, которая действует на тело со стороны опоры или подвеса, называется силой реакции опоры или силой натяжения подвеса.

Закон Гука можно записать в другом виде. Рассмотрим деформацию растяжения стержня. При действии заданной силы F, абсолютная деформация стержня  зависит от его первоначальной длины , тогда как относительная деформация  уже не зависит от длины стержня, но зависит от площади поперечного сечения S. Если вместо силы ввести напряжение , то при заданном напряжении относительное удлинение будет зависеть только от упругих свойств материала. И тогда закон Гука примет следующий вид:

, или .

(2.3)

Величина Е называется модулем Юнга. Модуль Юнга зависит только от материала. Установим физический смысл модуля Юнга. Как видно из формулы (2.3),  при . В этом случае . Следовательно, модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в два раза (если бы для такой большой деформации выполнялся закон Гука). Из (2.3) видно также, что в системе единиц СИ модуль Юнга измеряется в паскалях ( ). Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, , а для резины приблизительно , то есть на пять порядков меньше.

Конечно, закон Гука даже в усовершенствованной Юнгом форме не описывает всего, что происходит с твердым веществом под воздействием внешних сил. Представьте себе резиновую ленту. Если растянуть ее не слишком сильно, со стороны резиновой ленты возникнет возвращающая сила упругого натяжения, и как только вы ее отпустите, она тут же соберется и примет прежнюю форму. Если растягивать резиновую ленту дальше, то рано или поздно она утратит свою эластичность, и вы почувствуете, что сила сопротивления растяжению уменьшилась. Значит, вы перешли так называемый предел эластичности материала. Если тянуть резину и дальше, через какое-то время она вообще порвется, и сопротивление исчезнет полностью. Это значит, что пройдена так называемая точка разрыва. Иными словами, закон Гука действует только при относительно небольших сжатиях или растяжениях.

Примеры действия упругой силы

Пример 1        

Пример 2

Пример 3

Пример 4

Пример 5

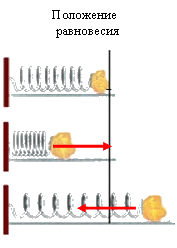
Действующая на тело упругая сила со стороны деформированной пружины заставляет тело совершать колебания около положения равновесия

Прыжок на упругом канате в грот. На человека со сторон каната действует сила упругости каната

Воздушные гимнасты. Сила тяжести, действующая на гимнастов, скомпенсирована упругой силой деформированных канатов

Полет теннисного мяч обусловлен импульсом силы упругости, подействовавшей на него со стороны упруго деформированной сетки ракетки

Прыжок спортсмена вверх обусловлен действием силы упругости со стороны деформированной доски

Гравитационные силы (силы тяготения). Гравитационное взаимодействие описывается законом всемирного тяготения, открытым Ньютоном в 1682 г. Ньютон получил свой закон, основываясь на трех законах Кеплера, установленных на основании астрономических наблюдений Тихо Браге за движением планет Солнечной системы. Согласно этим законам:

 траектории всех планет имеют форму эллипса, в одном из фокусов которого находится Солнце;

 площади, описываемые радиус-вектором планеты за равные промежутки времени, одинаковы;

 для всех планет отношение квадрата периода обращения к кубу большой полуоси эллипса имеют одно и то же значение:

.

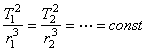Орбиты большинства планет мало отличаются от круговой. Рассмотрим две планеты, движущиеся вокруг Солнца по круговым орбитам. Сила, сообщающая планетам нормальное ускорение, согласно второму закону:

.

Отношение сил, действующих на планеты, 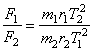. С учетом третьего закона Кеплера,

.

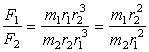Это соотношение, справедливое для любых планет, возможно, если

,

где С – постоянная, одинаковая для всех планет, r – расстояние от планеты до Солнца. Постоянная С не зависит от массы планеты, а может зависеть от параметров, характеризующих Солнце. Но Солнце и планеты выступают во взаимодействии как равноправные тела, поэтому, если сила  пропорциональна массе планеты m, то она должна быть пропорциональна и массе Солнца М. На этом основании можно записать силу тяготения в форме

,

(2.4)

где  – гравитационная постоянная. Так как Солнце и планеты отличаются только массами, то естественно считать, что это выражение применимо к определению силы взаимодействия между любыми телами.

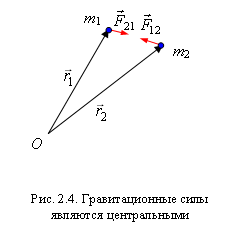
Закон всемирного тяготения формулируется следующим образом: сила тяготения между двумя материальными точками пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Из формулы (2.4) видно, что гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, имеющих массы, равные единице массы, и находящихся друг от друга на расстоянии, равном единице длины. Числовое значение гравитационной постоянной установлено экспериментально. Впервые это сделал английский ученый Кавендиш с помощью крутильного динамометра (крутильных весов). В системе единиц СИ гравитационная постоянная имеет значение . Следовательно, две материальные точки массой 1 кг каждая, находящиеся друг от друга на расстоянии 1 м, взаимно притягиваются гравитационной силой, равной . Изложенные соображения нельзя рассматривать как вывод закона всемирного тяготения, они являются лишь иллюстрациями к соображениям Ньютона.

Гравитационные силы являются силами притяжения: на каждую массу действует сила притяжения со стороны другой массы. Таким образом, это всегда две силы, направленные по прямой, соединяющие их центры, поэтому эти силы являются центральными (рис. 2.4). В векторной форме силу, действующую на тело массой  со стороны тела массой , можно записать в следующем виде:

,

где , .

Закон всемирного тяготения Ньютона справедлив только для точечных масс, то есть для таких тел, размеры которых малы по сравнению с расстоянием между ними. Однако его можно применить и для вычисления сил притяжения тел конечных размеров. Для этого нужно мысленно разбить тело на отдельные элементы, которые можно считать материальными точками, и затем векторно сложить все силы, создаваемые этими элементами. Именно таким способом можно показать, что закон Ньютона можно применить к однородным шарам, считая, что вся масса шара сосредоточена в его центре.

Основное физическое содержание второго закона Ньютона состоит в том, что сила гравитационного притяжения тел пропорциональна их инертным массам, то есть массам, характеризующим инертные свойства тел. Но инерция и способность к гравитационным взаимодействиям представляют разные свойства материи и, следовательно, гравитационное взаимодействие должно определяться гравитационными массами. Однако с высокой степенью точности экспериментально установлено равенство инертных и гравитационных масс.

Сила тяжести. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. По закону всемирного тяготения она равна . Тогда, согласно второму закону Ньютона:

,

где  – масса Земли;  – радиус Земли,  – ускорение тела массой m. Таким образом, сила тяжести . Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Модуль ускорения свободного падения g находят по формуле:

.

(2.5)

Из (2.5) следует, что ускорение свободного падения не зависит от массы  падающего тела, то есть для всех тел в данном месте Земли оно одинаково. Поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. По этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.

Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле:

.

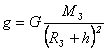Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на . Следовательно, вблизи Земли (до высот порядка нескольких километров) сила тяжести практически не изменяется, а поэтому свободное падение тел вблизи Земли является движением равноускоренным.

Вес тела. Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору (или подвес), неподвижную относительно данного тела. Если сила тяжести является результатом взаимодействия тела с Землей, то вес тела появляется в результате совсем другого взаимодействия – взаимодействия тела и опоры (или подвеса). Поэтому вес обладает особенностями, существенно отличающими его от силы тяжести. В частности, эти силы приложены к разным телам, и, кроме того, вес существенно зависит от ускорения, с которым движутся совместно опора (подвес) и тело.

Гравитационное поле. Закон всемирного тяготения основан на теории дальнодействия, согласно которой действие одного тела на другое передается мгновенно (то есть с бесконечно большой скоростью) без участия среды. Согласно современным представлениям всякое взаимодействие тел на расстоянии осуществляется посредством материальной среды, называемой полем, и передается с конечной скоростью, которая не может быть больше скорости света. Гравитационное взаимодействие между телами, описываемое законом всемирного тяготения, осуществляется посредством гравитационного поля (поля тяготения). В каждой точке поля тяготения на помещенное туда тело действует сила тяготения, пропорциональная массе этого тела. Сила тяготения не зависит от среды, в которой находятся тела.

С этих позиций гравитационное взаимодействие представляется следующим образом. Всякое тело массой М создает вокруг себя гравитационное поле. Если в какую-либо точку поля поместить пробную массу m, то на нее будет действовать сила F, зависящая от свойств поля в этой точке и от величины массы пробного тела m.

Для количественной характеристики поля тяготения вводится физическая величина, называемая напряженностью гравитационного поля g. Напряженность гравитационного поля численно равна силе, действующей на единичную массу, помещенную в данную точку поля:

.

Таким образом, напряженность гравитационного поля зависит только от массы М тела, создающего поле, и от расстояния от этого тела до точки наблюдения, но не зависит от массы пробного тела m. По величине напряженность гравитационного поля совпадает с ускорением свободного падения пробного тела.

Первая космическая скорость. Для того чтобы тело двигалось вокруг Земли по круговой орбите, сила тяготения должна сообщать ему нормальное ускорение :

.

Отсюда . Скорость  называют первой космической скоростью. Приведенное значение получается, если принять g = 9,8 м/с, а радиус Земли R = 6370 км. Такое движение возможно, когда нет сил сопротивления воздуха, то есть на высоте более 100 км.

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики.

Примеры

Это интересно!

Пример 1

Пример 2

Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии . Это расстояние приблизительно в 60 раз превышает радиус Земли R_З. Следовательно, ускорение свободного падения , обусловленное земным притяжением, на орбите Луны составляет 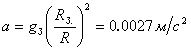, где  – ускорение свободного падения на поверхности Земли. С таким ускорением, направленным к центру Земли, Луна движется по орбите. Период обращения Луны вокруг Земли составляет 27,3 суток. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.

Собственное гравитационное поле Луны определяет ускорение свободного падения  на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение свободного падения на Луне определится выражением:

.

В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.

Факты опубликованы на сайте http://nauka.relis.ru

Г. НИКОЛАЕВ.

По материалам журнала «Bild der Wissenschaft» (Германия).

Факт влияния силы тяготения Луны на многие процессы, идущие на Земле, не вызывает сомнений. С притяжением Луны связаны морские приливы. На суше отливы и приливы проявляют себя на уровне почвенной влаги. Когда наша спутница проходит через небосвод, на материках – в грунте, в скалах – так же, как в океанах, проходит приливная волна. Она невысока – всего до полуметра. Люди не чувствуют, что под ними целый континент «вздувается и опадает», но деревья позволяют измерять этот эффект. Стволы изменяют свой диаметр. Профессор Е. Цурхер из Швейцарии измерял диаметр ствола молодых елей. В зависимости от фазы Луны толщина стволов изменялась, правда, лишь на доли миллиметра. Изменения размеров ствола происходят циклически: два раза в месяц они принимают максимальное значение и два раза – минимальное. Такие колебания исследователи объясняют тем, что в клетки растения поступает то больше соков, то меньше – своеобразный отголосок приливов и отливов.

Попытаемся представить, что случилось бы на Земле, если бы у нашей планеты не оказалось Луны. Соответствующее математическое исследование провел французский астроном Ж. Ласкар. Главный вывод, который сделал ученый, - притяжение Луны стабилизирует климат нашей планеты. Одним только своим присутствием по соседству с Землей Луна ограничивает колебания оси земного шара относительно плоскости эклиптики. В настоящее время ось наклонена к этой плоскости на 23 градуса. Наклон оси, как известно, определяет смену времен года, то есть количество солнечной энергии, приходящей на те или иные широты в северном и южном полушариях.

Расчеты Ж. Ласкара показали, что, не будь Луны, ось земного шара могла бы менять свой наклон по отношению к плоскости эклиптики, причем в значительных пределах – от 0 до 85 градусов. Тогда, например, при угле наклона 85 градусов Солнце было бы почти в зените над Северным полюсом, южное же полушарие надолго оставалось бы погруженным во тьму. Разность температур в полушариях вызвала бы чудовищные по силе ураганы и дожди, наверное, куда более сильные, чем библейский потоп.

Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. Если из пушки, стоящей на высокой башне выстрелить, то ядро, описав дугу, может упасть на Землю. При увеличении начальной скорости ядра дальность полета увеличивается. Наконец, можно выстрелить так, что ядро никогда не упадет, то есть превратится в искусственный спутник Земли.

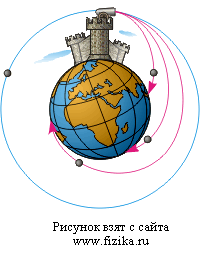
Движение спутника можно рассматривать как свободное падение. При этом скорость спутника (первая космическая скорость) настолько велика, что он движется по круговой траектории вокруг Земли.

Силы трения. Первые исследования трения, о которых мы знаем, были проведены Леонардо да Винчи примерно 500 лет назад. Он измерял силу трения, действующую на деревянные параллелепипеды, скользящие по доске, причём, ставя бруски на разные грани, определял зависимость силы трения от площади опоры. Но работы Леонардо да Винчи стали известны уже после того, как классические законы трения были вновь открыты французскими учёными Амонтоном и Кулоном в XVII–XVIII вв.

Леонардо да Винчи, 1452–1519

Великий итальянский художник и скульптор, исследователь, инженер-изобретатель, архитектор и механик, химик, ботаник и анатом, философ, поэт и музыкант.

Талантливый человек во всем талантлив, но лишь немногие гении были гениальны во всем, что бы они ни делали, и, пожалуй, за всю историю человечества только один человек – Леонардо да Винчи – заслуживает звания абсолютно универсального гения. Как художник, скульптор и инженер он превосходил своих современников. Как ученый он обогнал свою эпоху на века. Среди бесчисленных научных достижений и первая формулировка законов трения. Леонардо (1519) утверждал, что сила трения, возникающая при контакте тела с поверхностью другого тела, пропорциональна нагрузке, направлена против направления движения и не зависит от площади контакта. Модель Леонардо была переоткрыта через 180 лет Г. Амонтоном и получила окончательную формулировку в работах Ш.О. Кулона (1781).

Силы трения возникают на поверхностях соприкасающихся тел и всегда направлены вдоль поверхности соприкосновения. Одна из причин возникновения этой силы – шероховатость поверхности соприкасающихся тел. Сила трения покоя удерживает вбитый гвоздь, не дает развязаться банту и даже помогает нам ходить. Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиною с каменную глыбу или малы, как песчинки, никогда не удержатся одно на другом: всё будет скользить и катиться, пока не окажется на одном уровне. Не будь трения, Земля представляла бы шар без неровностей.

Поверхность твёрдого тела обычно обладает неровностями. Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны «горы» и «впадины» размером в  м. При сжатии тел соприкосновение происходит только в самых высоких местах и площадь реального контакта значительно меньше общей площади соприкасающихся поверхностей. Как образно выразился один из основоположников трибологии (науки о трении), Ф. Боуден, «наложение двух твердых тел одного на другое подобно наложению швейцарских Альп на перевернутые австрийские Альпы – площадь контакта оказывается очень малой». Однако при сжатии остроконечные «горные пики» пластически деформируются и подлинная площадь контакта увеличивается пропорционально приложенной нагрузке. Именно сопротивление относительному сдвигу этих контактных зон и является основным источником трения движения. Само сопротивление сдвигу при идеальном контакте определяется межмолекулярным взаимодействием, зависящим от природы контактирующих материалов. Давление в местах соприкосновения может быть очень большим, и там возникает пластическая деформация. При этом площадь контакта увеличивается, а давление падает. Так продолжается до тех пор, пока давление не достигнет определённого значения, при котором деформация прекращается. Поэтому площадь фактического контакта оказывается пропорциональной сжимающей силе.

Различают три вида трения: трение покоя, трение скольжения и трение качения. Если тела неподвижны друг относительно друга, то говорят о трении покоя, при относительном перемещении – о трении скольжения. Если одно из тел катится по поверхности другого без проскальзывания, возникает трение качения.

Строго говоря, сила , с которой одно тело действует на другое, направлена под некоторым углом к поверхности. Эту силу можно разложить на две составляющие: силу, направленную по касательной к поверхности соприкосновения , и силу реакции опоры , направленную по нормали к поверхности соприкосновения. Экспериментально установлено (закон Кулона–Амонтона), что эти составляющие связаны между собой: . Коэффициент пропорциональности зависит от рода соприкасающихся поверхностей, их обработки и не зависит от площади трущихся поверхностей. В случаях трения покоя и трения скольжения коэффициент m имеет разные значения.

Сила трения покоя не является однозначной величиной. Будем пытаться сдвинуть с места тело, потянув за трос с пружинным динамометром. При малом натяжении троса тело остается на месте: силы, развиваемой пружиной динамометра, недостаточно. Говорят, что вдоль контактирующих поверхностей действует сила трения покоя, уравновешивающая приложенную силу. Постепенно увеличиваем упругую силу, приложенную к телу. В какой-то момент она оказывается достаточной для того, чтобы сдвинуть тело с места. В этот момент сила трения покоя достигает своего максимального значения, то есть сила трения покоя всегда меньше или равна этому максимальному значению:

.

При нагружении тела различными гирями изменяется сила нормального давления, а следовательно, и равная ей сила реакции опоры N. Можно показать, что . Величина  называется коэффициентом трения покоя.

Если тело под действием приложенной силы движется равномерно, то это говорит о том, что эта сила уравновешивается силой трения скольжения. Исследовав величину силы трения скольжения  при различных условиях, можно показать, что она, как и сила трения покоя, зависит от силы реакции опоры и качества трущихся поверхностей. Кроме того, она зависит от площади соприкосновения и мало зависит от скорости относительного движения трущихся тел. Поэтому сила трения скольжения можно вычислить по формуле:

.

m – коэффициент трения скольжения, он несколько меньше коэффициента трения покоя. Сила трения покоя у шлифованных поверхностей меньше, чем у грубо обработанных. По-видимому, основную роль в возникновении силы трения покоя при грубой обработке играют зацепления выступов, тогда как трение скольжения возникает в результате пластических деформаций микровыступов и их частичного разрушения. Уменьшение зацепления и прилипания поверхностей уменьшает силу трения. В технике для уменьшения трения используется смазка. Трение скольжения также заменяют трением качения, устанавливая шариковые или роликовые подшипники.

Трение качения. Если по поверхности катится цилиндр или колесо, то возникает сила трения качения. Сила трения качения значительно меньше силы трения скольжения. Как показывает опыт, сила трения качения пропорциональна силе нормального давления и обратно пропорциональна радиусу цилиндра (или колеса):

,

где k – коэффициент трения качения. Это выражение справедливо, когда нет проскальзывания при качении.

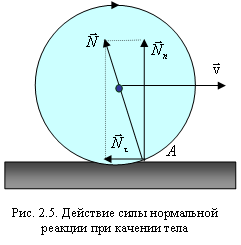
Причина появления трения качения заключается в следующем. Под действием силы тяжести круглое твердое тело (например, шар или колесо), находящееся на плоской поверхности, деформируется, вследствие чего оно опирается не на одну точку, а на площадку больших или меньших размеров. Это приводит к тому, что, когда тело начинает катиться, точка А приложения силы реакции опоры смещается немного вперед от вертикали, проходящей через центр тяжести тела, а линия действия силы реакции опоры N отклоняется немного назад от этой вертикали (рис. 2.5). При этом нормальная составляющая  силы реакции опоры компенсирует силу тяжести, а нескомпенсированная тангенциальная составляющая  направлена против движения тела и играет роль силы трения качения .

Трением сопровождается любое движение. В большинстве случаев трение приводит к износу машин и механизмов, вынуждая бороться с ним всеми доступными способами. Однако далеко не всегда оно оказывается вредным. Трение играет как полезную, так и вредную роль.

Примеры

Пример 1         

Пример 2

Пример 3

Пример 4

Пример 5

Пример 6

Трение между подошвой и землей позволяет человеку ходить. При одном и том же весе человека сцепление стертой кожаной подошвы с асфальтом будет слабее, чем подошвы из пористой резины. Значит, во втором случае сила трения и, соответственно, коэффициент трения больше. При ходьбе по асфальту в обуви на мягкой резиновой подошве коэффициент трения составляет примерно 0,5. Это означает, что человека весом, скажем, 500 Ньютонов (то есть массой около 50 килограммов) можно сдвинуть с места горизонтальной силой 250 Ньютонов. В гололед коэффициент трения может уменьшиться раз в 25, достигая величины 0,02. Каждый, вероятно, может припомнить случай, когда на скользком месте при попытке сделать очередной шаг вынесенная вперед нога неожиданно скользит вперед, а человек начинает падать назад или вбок. Чтобы понять, почему это происходит, рассмотрим с точки зрения механики в деталях, как производится отдельный шаг. Человек наклоняется и почти одновременно приподнимает одну ногу, перемещая вперед свой центр масс. Возникающий при этом момент силы тяжести его тела относительно точки опоры – точки соприкосновения оставшейся сзади ноги с землей – вызывает как бы падение человека вперед. Успев в начальной стадии этого падения пяткой «передней» ноги коснуться земли, человек выполняет шаг. Пятка воспринимает составляющую силы реакции опоры, направленную вдоль вытянутой ноги. Эта составляющая, в свою очередь, раскладывается на две: перпендикулярную к поверхности, по которой вы идете (нормальную), и параллельную этой поверхности (тангенциальную). Нормальная составляющая, умноженная на коэффициент трения, как раз и создает силу трения между ногой и поверхностью. Тангенциальная составляющая стремится сдвинуть ногу вперед, а сделать это ей мешает сила трения.

Чем длиннее шаг делает человек, тем сильнее он наклоняется вперед. С ростом угла наклона туловища перпендикулярная земле составляющая уменьшается, а параллельная увеличивается. Соответственно уменьшается сила трения, и увеличивается сила, сдвигающая ногу вперед. При некоторой ширине шага эта сдвигающая сила может превысить силу трения: нога проскользнет вперед, а туловище человека начнет опрокидываться назад. Это же происходит, когда носок оставшейся сзади ноги начинает скользить назад из-за того, что сила трения уже не может противодействовать параллельной (сдвигающей) силе.

Проскальзывание каблука в зоне контакта с опорой, то есть скольжение, как и всякое трение, приводит к выделению тепла, нагреву подошвы обуви и поверхности опоры. Этого тепла достаточно, чтобы в гололед началось оплавление ледяной поверхности, резко уменьшающее и без того малый коэффициент трения. Если поверхность льда прикрыта снегом, нагрузка передается на лед через прослойку снежинок – кристалликов замерзшей воды с относительно большой суммарной поверхностью. На спрессованной массе снежинок появляется пленка воды, играющая роль смазки. Трение из сухого превращается в жидкое, уменьшаясь при этом в десятки раз. Возникает опасность падения.

По заявлению членов экипажа «Апполон – 12» Ч. Конрода и А. Бина, по Луне легко ходить, но они часто теряли равновесие, так как даже при легком наклоне вперед можно упасть. Это можно объяснить следующим образом. Устойчивость ходьбы человека определяется силой трения между подошвой обуви и почвой. Поскольку сила тяжести на Луне в 6 раз меньше, чем на Земле, то там при ходьбе возникала и малая сила трения.

Не надо думать, что трение всегда препятствует движению – часто оно ему способствует. При прокручивании колёс автомобиля сила трения шин о поверхность земли, препятствуя их проскальзыванию, действует со стороны дороги и направлена вперёд, обеспечивая движение автомобиля. Чем сильнее трение, тем больше соответствующая сила, поэтому его стараются не уменьшать, а увеличивать: покрытие дороги делают шероховатым, наносят на поверхность шины рельефные рисунки (протекторы)

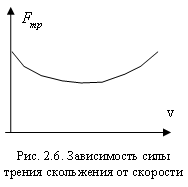
При движении тела по окружности с постоянной скоростью сила трения покоя сообщает ему нормальное ускорение. Само тело остается неподвижным относительно вращающегося диска. При увеличении скорости вращения до критического значения тело соскользнет с диска

Трение скольжения возникает при скольжении одного тела по поверхности другого. На рисунке показано движение лыжника на трассе слалома. Наличие силы трения замедляет скорость его движения и способствует успешному прохождению трассы

Почему звучит скрипичная струна, когда по ней ведут смычком? Ведь смычок движется поступательно, а колебания струны периодические. Хорошо известно, что сила трения скольжения практически не зависит от скорости. Однако именно благодаря очень слабой зависимости силы трения от скорости звучит скрипичная струна. Качественный вид зависимости силы трения смычка о струну показан на рис. 2.6. Благодаря силе трения покоя струна захватывается смычком и смещается из положения равновесия. Когда сила упругости превысит силу трения, струна оторвется от смычка и устремится к положению равновесия со все возрастающей скоростью. Скорость струны относительно движущегося смычка будет возрастать, сила трения увеличится и в определенный момент станет достаточной для захвата струны. Затем процесс повторится вновь. Таким образом, движущийся с постоянной скоростью смычок вызовет незатухающие колебания струны. Подобные, но уже вредные колебания могут возникнуть при обработке металла на токарном станке вследствие трения между снимаемой стружкой и резцом. И если смычок натирают канифолью, чтобы сделать зависимость силы трения от скорости более резкой, то при обработке металла приходится действовать наоборот (выбирать специальную форму резца, смазку и т.п.). Так что важно знать законы трения и уметь ими пользоваться.

Тефлоновое покрытие имеет низкий коэффициент трения с пищевыми продуктами, что обеспечивает отсутствие их пригорания. На обычной сковороде взаимодействие с поверхностью более сильное и продукты пригорают