2.3. Второй закон ньютона

Из опыта следует, что в инерциальных системах отсчета ускорение тела пропорционально векторной сумме всех действующих на него сил и обратно пропорционально массе тела:

.

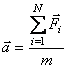Второй закон Ньютона выражает связь между равнодействующей всех сил и вызываемым ей ускорением:

.

(2.1)

Уравнение (2.1) называется уравнением движения материальной точки.

Масса тел может изменяться при движении, например, при полете ракеты выгорает топливо. В этом случае второй закон Ньютона можно записать в более общей форме: . Произведение массы на скорость  называется импульсом. Следовательно, уравнение движения принимает вид:

.

(2.2)

Здесь  – изменение импульса материальной точки за время . Устремим промежуток времени  к нулю:

,

тогда получим

.

Среди экстремальных видов развлечений особое место занимают прыжки с «тарзанки», или «банджи-джампинг». В местечке Джеффри Бей находится самая большая из зарегистрированных «тарзанок» – 221 м. Она даже занесена в Книгу рекордов Гиннеса. Длина веревки рассчитывается так, чтобы человек прыгая вниз, останавливался у самой кромки воды или только касался ее. Прыгающего человека удерживает упругая сила деформированного каната. Обычно тросом служат множество сплетенных вместе резиновых жил. Так что при падении трос пружинит, не давая ногам прыгуна оторваться и добавляя прыжку дополнительные ощущения. В полном соответствии со вторым законом Ньютона  увеличение времени взаимодействия прыгуна с канатом приводит к ослаблению силы, действующей со стороны каната на человека. Фотография взята с сайта www.zambezi.ru

Для того, чтобы при игре в волейбол принять мяч, летящий с большой скоростью, необходимо перемещать руки по направлению движения мяча. При этом увеличивается время взаимодействия с мячом, а, следовательно, в полном соответствии со вторым законом Ньютона уменьшается величина силы, действующей на руки.

Представленный в такой форме второй закон Ньютона содержит новую физическую величину – импульс. При скоростях, близких к скорости света в вакууме, импульс становится основной величиной, измеряемой в экспериментах. Поэтому уравнение (2.2) является обобщением уравнения движения на релятивистские скорости.

Как видно из уравнения (2.2), если 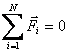, то  постоянная величина, отсюда следует, что  постоянна, то есть импульс, а с ним и скорость свободно движущейся материальной точки постоянны. Таким образом, формально первый закон Ньютона является следствием второго закона. Почему же тогда он выделяется в самостоятельный закон? Дело в том, что уравнение, выражающее второй закон Ньютона, только тогда имеет смысл, когда указана система отсчета, в которой оно справедливо. Выделить же такую систему отсчета позволяет первый закон Ньютона. Он утверждает, что существует система отсчета, в которой свободная материальная точка движется без ускорения. В такой системе отсчета движение всякой материальной точки подчиняется уравнению движения Ньютона. Таким образом, по существу, первый закон нельзя рассматривать как простое логическое следствие второго. Связь между этими законами более глубокая.

Из уравнения (2.2) следует, что , то есть бесконечно малое изменение импульса за бесконечно малый промежуток времени  равно произведению , называемому импульсом силы. Чем больше импульс силы, тем больше изменение импульса.

Примеры

Пример 1             

Пример 2