- •Содержание
- •5.1. Неинерциальные системы отсчета
- •Введение
- •1. Кинематика материальной точки
- •1.1. Системы отсчета
- •1.2. Материальная точка
- •1.3. Описание движения
- •1.4. Относительность перемещений и скоростей
- •1.5. Кинематика движения точки по окружности
- •2. Динамика материальной точки и системы материальных точек
- •2.1. Первый закон ньютона. Инерциальные системы отсчета
- •2.2. Сила. Масса тела
- •2.3. Второй закон ньютона
- •2.4. Типы сил
- •2.5. Роль начальных условий
- •2.6. Третий закон ньютона
- •2.6. Третий закон ньютона
- •2.7. Второй закон ньютона для системы материальных точек. Закон сохранения импульса
- •2.8. Теорема о движении центра масс системы материальных точек
- •2.9. Принцип относительности галилея. Преобразования галилея
- •3. Законы сохранения
- •3.1. Закон сохранения импульса
- •3.2. Движение тел с переменной массой
- •3.3. Работа и энергия
- •3.4. Энергия
- •3.5. Кинетическая энергия
- •3.6. Примеры на вычисление работы
- •3.7. Потенциальные и непотенциальные силы
- •3.8. Потенциальная энергия частицы в поле
- •3.9. Закон сохранения полной механической энергии частицы
- •3.10. Силы и потенциальная энергия
- •3.11. Одномерное движение частицы
- •4. Динамика твердого тела
- •4.1. Вращательное движение твердого тела
- •4.2. Закон сохранения момента импульса
- •4.3. Механическое равновесие
- •4.4. Кинетическая энергия вращательного движения твердого тела
- •5. Неинерциальные системы отсчета
- •5.1. Неинерциальные системы отсчета
- •5.2. Силы инерции
- •5.3. Нахождение сил инерции
- •5.4. Вращающиеся системы отсчета
- •5.5. Сила кариолиса
- •6. Гидродинамика
- •6.1. Кинематическое описание движения жидкости
- •6.2. Уравнение неразрывности
- •6.3. Стационарное движение идеальной жидкости. Уравнение бернулли
- •6.4. Формула торричелли
- •6.5. Реакция вытекающей струи
- •6.6. Движение тел в жидкостях и газах
- •6.7. Эффект магнуса
- •7. Гармонические, затухающие, вынужденные колебания. Резонанс
- •7.1. Колебательное движение
- •7.2. Гармонические колебания
- •7.3. Энергия гармонического осциллятора
- •7.4. Векторная диаграмма и сложение колебаний
- •7.5. Затухающие колебания
- •7.6. Вынужденные колебания
- •7.7. Резонанс
- •7.8. Автоколебания
- •8. Упругие волны
- •8.1. Образование волн
- •8.2. Уравнение плоской упругой волны
- •8.3. Энергия, переносимая упругой волной
- •8.4. Эффекты сложения волн. Стоячие упругие волны
- •8.5. Звуковые волны
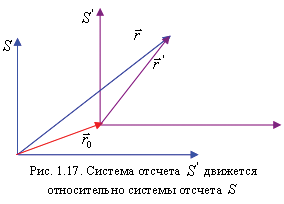
1.4. Относительность перемещений и скоростей
|
![]() ,
,
где
–
скорость материальной точки в системе
отсчета S,
![]() –
скорость материальной точки в системе
отсчета
,
–
скорость движения системы отсчета
относительно
системы отсчета S.
–
скорость материальной точки в системе
отсчета
,
–
скорость движения системы отсчета
относительно
системы отсчета S.
Взяв производную от обеих частей последнего выражения по времени, найдем формулу преобразования ускорения:
![]() .
.
Отсюда видно, в частности, что при
![]()
![]() ,
то есть при движении
-системы
отсчета без ускорения относительно
S-системы отсчета ускорения точки
в обеих системах отсчета будут одинаковы.
,
то есть при движении
-системы
отсчета без ускорения относительно
S-системы отсчета ускорения точки
в обеих системах отсчета будут одинаковы.
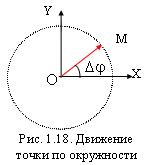
1.5. Кинематика движения точки по окружности
Положение частицы, движущейся по
окружности, можно задать углом
![]() ,
который образует радиус-вектор с
каким-либо неизменным направлением,
например, осью X.
,
который образует радиус-вектор с
каким-либо неизменным направлением,
например, осью X.
|
![]() .
.
Направление вектора угловой скорости определяется по правилу правого винта. Если рукоятку винта поворачивать по направлению движения точки, то его поступательное движение покажет направление вектора угловой скорости.
При вращении частицы с постоянной по
модулю скоростью угловую скорость
называют также угловой частотой вращения.
Она показывает, на какой угол поворачивается
радиус-вектор, определяющий положение
материальной точки, за единицу времени.
Величина
![]() дает
число оборотов в единицу времени и
называется частотой. Время, за которое
частица совершает полный оборот,
называется периодом вращения
дает
число оборотов в единицу времени и
называется частотой. Время, за которое
частица совершает полный оборот,
называется периодом вращения
![]() .
.
Вектор угловой скорости
![]() может
изменяться как за счет изменения скорости
вращения тела, так и за счет поворота
оси вращения в пространстве. Изменение
вектора угловой скорости со временем
характеризуется угловым ускорением.
Пусть за время
вектор
получает
приращение
может
изменяться как за счет изменения скорости
вращения тела, так и за счет поворота
оси вращения в пространстве. Изменение
вектора угловой скорости со временем
характеризуется угловым ускорением.
Пусть за время
вектор
получает
приращение
![]() .
Тогда угловое ускорение определится
как
.
Тогда угловое ускорение определится
как
![]() .
.
Вектор углового ускорения частицы при неизменной ориентации оси вращения параллелен этой оси и направлен вдоль вектора или против него в зависимости от того, увеличивается или уменьшается угловая скорость.
Отдельные точки вращающегося тела имеют
различные линейные скорости
,
при этом скорость каждой из точек
непрерывно изменяет свое направление.
Можно показать, что модуль линейной
скорости точки зависит от угловой
скорости и от расстояния от этой точки
до оси вращения. Пусть за малый промежуток
времени
тело
повернулось на угол
.
Точка, находящаяся на расстоянии
![]() от
оси вращения, проходит при этом путь
от
оси вращения, проходит при этом путь
![]() .
Модуль линейной скорости точки равен
.
Модуль линейной скорости точки равен
![]() .
.
Таким образом, модули линейной и угловой скорости связаны соотношением
![]() .
.