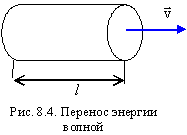
8.3. Энергия, переносимая упругой волной

Волновое движение сопровождается переносом энергии от источника колебаний в различные точки среды. Эта энергия складывается из кинетической энергии колеблющихся частиц и потенциальной энергии деформированных участков среды. Энергия, переносимая

волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Плотностью потока энергии или интенсивностью волны называется количество энергии, переносимое волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Пусть участок волнового фронта площадью  за время  переместился на расстояние , вследствие чего частицы среды в объеме цилиндра высотой  и основанием  приводятся в колебательное движение (рис.8.4). Обозначим через  среднюю энергию частиц, содержащихся в единичном объеме (плотность энергии). Если считать, что плотность энергии везде одинакова, то за время  через площадку  пройдет энергия . Тогда интенсивность волны равна

(8.3)

или, в векторной форме,

.

Вектор  называется вектором Умова. Он перпендикулярен фронту волны, указывает направление распространения энергии и по модулю равен плотности потока энергии. Объемную плотность энергии  можно выразить через энергию каждой частицы и количество частиц  в единице объема:

,

(8.4)

где  – плотность среды. Подставив это выражение в (8.3), получим:

.

Таким образом, интенсивность упругой волны пропорциональна квадрату амплитуды и квадрату собственной частоты колебаний частиц, плотности среды и скорости распространения волны.

8.4. Эффекты сложения волн. Стоячие упругие волны

Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн. Принцип суперпозиции утверждает, что движение, вызванное распространением сразу нескольких волн, есть снова некоторый волновой процесс. Таким процессом, например, является звучание оркестра. Оно возникает от одновременного возбуждения звуковых колебаний воздуха отдельными музыкальными инструментами. Замечательно, что при наложении волн могут возникать особые явления. Их называют эффектами сложения или, как еще говорят, суперпозиции волн. Среди этих эффектов наиболее важными являются интерференция и дифракция.

Интерференция – явление устойчивого во времени перераспределения энергии колебаний в пространстве, в результате которого в одних местах колебания усиливаются, а в других ослабляются. Это явление возникает при сложении волн с сохраняющейся во времени разностью фаз, так называемых когерентных волн. Интерференцию большого числа волн принято называть дифракцией. Принципиального различия между интерференцией и дифракцией нет. Природа этих явлений одна и та же. Мы ограничимся обсуждением только одного очень важного интерференционного эффекта, который заключается в образовании стоячих волн.

Необходимым условием образования стоячих волн является наличие границ, отражающих падающие на них волны. Стоячие волны образуются в результате сложения падающих и отраженных волн. Явления такого рода встречаются довольно часто. Так, каждый тон звучания любого музыкального инструмента возбуждается стоячей волной. Эта волна образуется либо в струне (струнные инструменты), либо в столбе воздуха (духовые инструменты). Отражающими границами в этих случаях являются точки закрепления струны и поверхности внутренних полостей духовых инструментов.

Каждая стоячая волна обладает следующими свойствами. Вся область пространства, в которой возбуждена волна, может быть разбита на ячейки таким образом, что на границах ячеек колебания полностью отсутствуют. Точки, расположенные на этих границах, называются узлами стоячей волны. Фазы колебаний во внутренних точках каждой ячейки одинаковы. Колебания в соседних ячейках совершаются навстречу друг другу, то есть в противофазе. В пределах одной ячейки амплитуда колебаний изменяется в пространстве и в каком-то месте достигает максимального значения. Точки, в которых это наблюдается, называются пучностями стоячей волны. Наконец, характерным свойством стоячих волн является дискретность спектра их частот. В стоячей волне колебания могут совершаться только со строго определенными частотами, и переход от одной из них к другой происходит скачком.

Рассмотрим простой пример стоячей волны. Предположим, что струна ограниченной длины  натянута вдоль оси ; концы ее жестко закреплены, причем левый конец находится в начале координат. Тогда координата правого конца будет . Возбудим в струне волну

,

распространяющуюся вдоль  слева направо. От правого конца струны волна отразится. Предположим, что это произойдет без потери энергии. В этом случае отраженная волна будет иметь ту же амплитуду и ту же частоту, что и падающая. Поэтому отраженная волна должна иметь вид:

.

Ее фаза содержит постоянную , определяющую изменение фазы при отражении. Поскольку отражение происходит на обоих концах струны и без потерь энергии, то в струне будут одновременно распространяться волны одинаковых частот. Поэтому при сложении  и  должна возникнуть интерференция. Найдем результирующую волну.

.

Это и есть уравнение стоячей волны. Из него следует, что в каждой точке струны происходят колебания с частотой . При этом амплитуда колебаний в точке  равна

.

Так как концы струны закреплены, то там колебания отсутствуют. Из условия  следует, что . Поэтому окончательно получим:

.

Теперь ясно, что в точках, в которых , колебания отсутствуют вовсе. Эти точки и являются узлами стоячей волны. Там же, где , амплитуда колебаний максимальна, она равна удвоенному значению амплитуды складываемых колебаний. Эти точки являются пучностями стоячей волны. В появлении пучностей и узлов как раз и заключается интерференция: в одних местах колебания усиливаются, а в других исчезают. Расстояние  между соседними узлом и пучностью находится из очевидного условия: . Поскольку , то . Следовательно, расстояние между соседними узлами .

Из уравнения стоячей волны видно, что множитель  при переходе через нулевое значение меняет знак. В соответствии с этим фаза колебаний по разные стороны от узла отличается на . Это означает, что точки, лежащие по разные стороны от узла, колеблются в противофазе. Все точки, заключенные между двумя соседними узлами, колеблются в одинаковой фазе.

Таким образом, при сложении падающей и отраженной волн действительно можно получить картину волнового движения, которая была охарактеризована ранее. При этом ячейки, о которых шла речь, в одномерном случае представляют собой отрезки, заключенные между соседними узлами и имеющие длину .

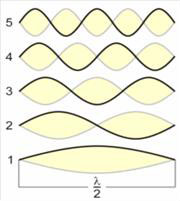
Рис. 8.5. Возможные колебания струны или столба воздуха в музыкальных инструментах

Убедимся, наконец, в том, что рассмотренная нами волна может существовать только при строго определенных частотах колебаний. Воспользуемся тем, что колебания на правом конце струны отсутствуют, то есть . Отсюда получается, что . Это равенство возможно, если , где  – целое произвольное положительное число.

Итак, оказывается, что , а, следовательно, и частота , связанная с  соотношением , могут принимать только следующие строго определенные значения: ; , где . Набор частот возможных колебаний называется спектром частот. Дискретность спектра частот является типичным свойством всех стоячих волн, резко выделяющимся в классической физике, в которой, казалось бы, все обречено изменяться непрерывным образом.

На рис. 8.5 приведены возможные колебания струны. Реальные колебания составляются из всех возможных, отвечающих разным значениям n. Каждая из составляющих даёт свой обертон. Обертонами называются высшие гармонические тоны, сопровождающие основной тон, соответствующий , и обусловливающие собою так называемый оттенок или тембр звука.