7.3. Энергия гармонического осциллятора

Во время колебательных процессов происходит периодическое превращение потенциальной энергии системы в кинетическую. Например, отклонив математический маятник в сторону и, следовательно, подняв его на высоту h, ему сообщают потенциальную энергию . Она полностью переходит в кинетическую энергию движения , когда груз проходит положение равновесия и скорость его максимальна. При колебаниях пружинного маятника кинетическая энергия движения груза переходит в потенциальную энергию деформированной системы. Величина полной энергии колеблющейся системы в любой момент времени равна сумме ее кинетической и потенциальной энергии:

или

	.		(7.2)

Поскольку скорость – это первая производная от координаты по времени, то

.

Учитывая, что  и подставив выражения для  и , получим:

.

То есть полная энергия системы, совершающей колебания, пропорциональна ее массе, квадрату амплитуды и квадрату собственной частоты. Так как силы, действующие на колеблющуюся частицу, являются консервативными, то ее механическая энергия остается постоянной. В процессе же колебаний происходит превращение кинетической энергии в потенциальную и обратно.

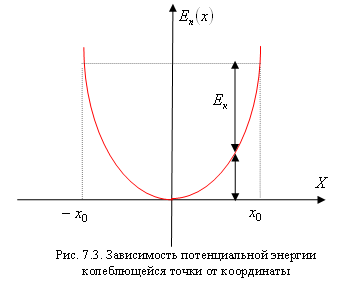
На рис. 7.3 приведен график зависимости потенциальной энергии от координаты частицы. С ростом x уменьшается кинетическая энергия и увеличивается потенциальная. Максимального значение потенциальная энергия достигает в поворотных точках , при этом кинетическая энергия равна нулю. Среднее за период значение кинетической энергии равно среднему за период значению потенциальной энергии.

7.4. Векторная диаграмма и сложение колебаний

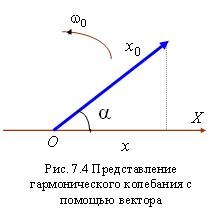
Существует очень наглядный геометрический способ представления гармонических колебаний, заключающийся в изображении колебаний в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой (рис. 7.4).

Выберем ось . Из точки О, взятой на этой оси, отложим вектор длины , образующий с осью угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца вектора на ось  будет меняться со временем по закону . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.

Векторная диаграмма дает возможность свести сложение колебаний к геометрическому суммированию векторов. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:

, .

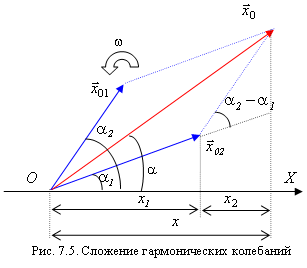
Представим оба колебания с помощью векторов  и  (рис. 7.5). Построим по правилу сложения векторов результирующий вектор . Легко увидеть, что проекция этого вектора на ось  равна сумме проекций слагаемых векторов . Следовательно, вектор  представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , что и векторы , , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой  и начальной фазой . По теореме косинусов квадрат амплитуды результирующего колебания будет равен

.

(7.3)

Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна

.

(7.4)

Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Формулы (7.3) и (7.4) можно, конечно, получить, сложив выражения для  и  аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.