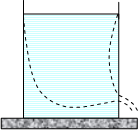
6.4. Формула торричелли

Рис. 6.3. К выводу формулы Торричелли

Применим уравнение Бернулли к истечению жидкости из небольшого отверстия в широком сосуде. Выделим трубку тока (рис. 6.3). В каждом сечении скорость и высоту над некоторым исходным уровнем можно считать постоянной. Давление в обоих сечениях равно атмосферному. Скорость перемещения открытой поверхности много меньше скорости истечения жидкости из отверстия , поэтому можно положить ее равной нулю. Тогда  

.

Отсюда , где . Эта формула называется формулой Торричелли и определяет скорость истечения жидкости из отверстия. Она получена для идеальной жидкости.

Из формулы Торричелли следует, что скорость истечения жидкости из отверстия одинакова для всех жидкостей и зависит лишь от высоты, с которой жидкость опустилась. Она оказывается равной скорости свободного падения тела с той же высоты. Для реальных жидкостей скорость будет меньше, она зависит от формы, размера отверстия и от вязкости жидкости

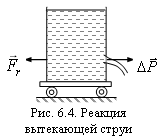
6.5. Реакция вытекающей струи

Струя жидкости, вытекающая из сосуда, уносит импульс:

,

где  – скорость истечения струи,  – масса жидкости, вытекшей за время . По третьему закону Ньютона сосуд получает от вытекающей жидкости за время Dt импульс , то есть испытывает действие силы (рис. 6.4).

.

Эта сила называется силой реакции вытекающей струи. Если сосуд стоит на тележке, то он будет двигаться в противоположном направлении под действием силы, модуль которой с учетом формулы Торричелли равен

.

Сила гидростатического давления на такой глубине равна , то есть меньше силы реакции вытекающей струи. Это объясняется тем, что при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.

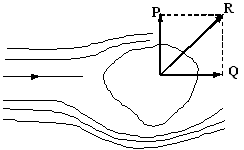
6.6. Движение тел в жидкостях и газах

Рис. 6.5. При движении тела в жидкости на него действуют силы

Идеальная жидкость является физической моделью, позволяющей понять суть явления в некотором приближении. Всем реальным жидкостям присуща вязкость или внутреннее трение, что приводит к появлению у них принципиально новых свойств. В частности, возникшее в жидкости движение после прекращения действия причин, его вызвавших, постепенно замедляется. Следовательно, жидкость при своем движении в трубе испытывает сопротивление. Такого рода сопротивление называют вязким, подчеркивая тем самым отличие от сопротивления в твердых телах. При движении тела в такой жидкости на него действуют силы. Равнодействующую этих сил обозначим через . Силу  можно разложить на две составляющих (рис. 6.5): . Силу  называют лобовым сопротивлением, а  – подъемной силой.

Если жидкость обладает вязкостью, то очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за трения последующие слои. По мере удаления от тела скорость уменьшается, то есть тело оказывается окруженным пограничным слоем жидкости, в котором скорость изменяется в направлении, перпендикулярном скорости. В нем действуют силы трения, которые в конечном итоге оказываются приложенными к телу и приводят к лобовому сопротивлению. Кроме того, из-за сил трения поток отрывается от поверхности тела, в результате чего позади тела возникают вихри. Вихри уносятся потоком и постепенно затухают вследствие трения. Давление в образующейся за потоком вихревой области оказывается пониженным, поэтому результирующая сил давления будет отлична от нуля, что в свою очередь обусловливает лобовое сопротивление. 

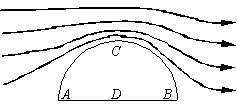
Рис. 6.6. Обтекание жидкостью полуцилиндра

Таким образом, лобовое сопротивление складывается из сопротивления трения и сопротивления давления. При этом сопротивление давления зависит от формы тела. Соотношение между сопротивлением трения и сопротивлением давления определяется свойствами жидкости. Лобовое сопротивление в идеальной жидкости отсутствует, в то время как подъемная сила может быть не равна нулю. Для возникновения подъемной силы вязкость жидкости не имеет существенного значения. Пусть идеальной жидкостью обтекается полуцилиндр (рис. 6.6). Вследствие полного обтекания линии тока будут симметричны относительно СД. Однако относительно прямой АВ картина будет несимметричной. Линии тока сгущаются вблизи точки С, поэтому давление там будет меньше, чем вблизи точки Д, благодаря чему и возникает подъемная сила. Аналогично подъемная сила возникает и в вязкой жидкости. Благодаря подъемной силе летают птицы и самолеты. Разрез крыла у них практически одинаковый: за счет сложной формы крыла создается разница обтекающих его сверху и снизу воздушных потоков, что позволяет телу подниматься вверх (рис. 6.7). Крыло в разрезе представляет собой сочетание двух выпуклых линий, причем кривизна верхнего контура больше, чем кривизна нижнего, в результате чего площадь верхней поверхности крыла больше площади его нижней поверхности. Именно эта малозаметная деталь конструкции и позволяет самолету весом в несколько сот тонн, разогнавшись, оторваться от взлетной полосы. Чтобы двум потокам сомкнуться за задней кромкой крыла, не образуя вакуума, воздух, обтекающий верхнюю поверхность крыла, должен двигаться быстрее относительно самолета, чем воздух, обтекающий нижнюю поверхность, поскольку ему нужно преодолеть большее расстояние. В результате, по мере набора самолетом скорости, возрастает направленная вверх разность давлений, и на крылья самолета действует нарастающая по мере разгона подъемная сила. Как только она начинает превышать силу гравитационного притяжения самолета к земле, самолет поднимается в воздух. Эта же сила удерживает самолет в горизонтальном полете: на крейсерской скорости подъемная сила уравновешивает силу тяжести.

Силой, поддерживающей самолет в воздухе, является подъемная сила. Лобовое сопротивление играет при этом вредную роль. Поэтому крыльям самолета и фюзеляжу придают обтекаемую форму. Такую же обтекаемую форму имеет тело летящей птицы, дельфина, дельтаплана, движущегося с огромной скоростью спортивного автомобиля.

Примеры

Пример 1        

Пример 2

Пример 3

Пример 4

Пример 5

Пример 6

Представьте себе небольшой реактивный самолет без крыльев, но с четырьмя колесами. Примерно так выглядит необычный автомобильчик Jetcar, производство которого налаживает немецкая фирма Jetcar Zukunftsfahrzeug GmbH

Тело дельфина имеет обтекаемую форму. Кривизна верхней части туловища больше, чем нижней

Так выглядит Citation X – самый быстрый реактивный самолет из числа «легких» бизнес-джетов. Он летит со скоростью чуть ниже скорости звука – свыше 960 км/ч

На рисунке изображены розовые фламинго в полете. Форма тела и крыльев птицы обеспечивают им подъемную силу и малое лобовое сопротивление в полете

Дельтаплан повторяет форму крыла самолета

Если пронаблюдать за взлетом самолетов в аэропорту вашего города, то можно заметить, что в разные дни самолеты разгоняются по взлетно-посадочной полосе в противоположных направлениях и садятся на нее также то в одном, то в другом направлении. Выбор направления зависит от направления ветра. При движении навстречу ветру, скорость самолета относительно Земли складывается со скоростью ветра относительно Земли. Поэтому при движении навстречу ветру скорость отрыва от земли, при которой подъемная сила начинает превышать силу тяжести, оказывается ниже, и самолету требуется меньшая длина разбега или торможения после посадки, то есть часть подъемной силы создается за счет энергии встречного ветра. Это снижает риск выхода за пределы взлетно-посадочной полосы и позволяет экономить горючее