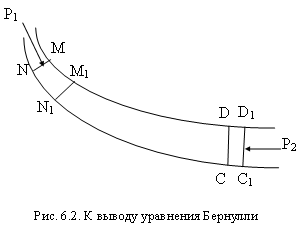
6.3. Стационарное движение идеальной жидкости. Уравнение бернулли

Рассмотрим идеальную жидкость. Идеальная жидкость – жидкость, плотность которой не зависит от давления и постоянна в любой пространственной области, а вязкость (внутреннее трение) отсутствует. При движении идеальной жидкости не происходит превращения механической энергии в тепловую, то есть механическая энергия жидкости сохраняется.

Рассмотрим стационарное течение идеальной жидкости в каком-либо потенциальном силовом поле, например в поле силы тяжести. Применим к этому течению закон сохранения энергии. Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объем MNDC. Пусть эта часть переместилась в бесконечно близкое положение  (рис. 6.2). При малом перемещении можно пренебречь различием площадей сечений MN и , CD и .

Вычислим работу А, совершаемую при этом силами давления. Силы давления, действующие на боковую поверхность трубки тока перпендикулярно к перемещению, работы не совершают. При перемещении границы MN в положение  силами давления совершается работа , где  – величина перемещения. Эту работу можно представить в виде  или , где  – масса жидкости в объеме , . При перемещении границы CD в положение  жидкость совершает работу против сил давления . Рассуждая аналогично, найдем , где  – масса жидкости в объеме .

Даниил Бернулли (Daniel Bernoulli), 1700–1782

Даниил Бернулли – один из наиболее выдающихся физиков и математиков своего времени. С 1725 г. по 1733 г. работал в Петербурге. Руководил работой кафедры чистой математики. Член Берлинской, Парижской, Петербургской и других академий наук, член Лондонского Королевского общества. Даниил Бернулли является одним из представителей настоящей потомственной династии научных гениев родом из Швейцарии. Отец Даниила – Иоганн Бернулли – был видным профессором математики в университете г. Гронинген.

Книга Даниила «Гидродинамика» (Hydrodynamica) была опубликована в 1738 г., практически одновременно с книгой Иоганна Бернулли «Гидравлика» (Hydraulica).

Если движение стационарно, то масса жидкости в объеме  не изменится, а потому из закона сохранения массы получим . Тогда для работы, совершаемой внешним давлением, получим:

.

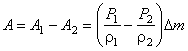Эта работа должна быть равна приращению  полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме  не изменилась. Поэтому приращение полной энергии равно разности энергий массы жидкости  в объемах  и . Обозначим через  энергию, приходящуюся на единицу массы жидкости, тогда . Приравнивая эту величину к работе А и сокращая на , получаем:

.

Отсюда следует, что вдоль одной и той же линии тока при стационарном течении идеальной жидкости величина  остается постоянной:

.

Это соотношение называется уравнением Бернулли. Оно было впервые опубликовано в 1738 году.

Энергия  складывается из кинетической энергии единицы массы жидкости  и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид:

Пусть жидкость течет по горизонтальной трубе. Тогда уравнение Бернулли примет вид:

(6.2)

Из выражения (6.2) следует, что в областях трубки с большей скоростью течения жидкости давление меньше. Согласно уравнению неразрывности струи (6.1) скорость течения жидкости больше в местах с меньшим сечением трубы, следовательно, давление по мере перехода к более узким ее участкам уменьшается. Образующийся при этом перепад давлений заставляет жидкость двигаться вдоль трубы с ускорением.

Пример

Эффект Бернулли можно наблюдать, сидя ненастным вечером дома у камина. Во время особенно сильных порывов ветра языки пламени взмывают вверх, в дымоход. Объяснить это можно так: когда скорость ветра у выходного отверстия трубы возрастает, давление в этом месте падает. Более высокое давление внутри дома и «выталкивает» пламя из камина в дымоход.