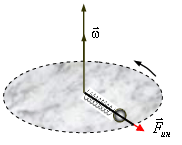
5.4. Вращающиеся системы отсчета

Рассмотрим более сложный пример неинерциальной системы отсчета. Пусть система отсчета вращается с постоянной угловой скоростью w вокруг неподвижной оси, то есть движется с ускорением относительно инерциальной системы отсчета.

Рассмотрим случай, когда тело покоится относительно вращающейся системы координат. Тогда его относительная скорость  и относительное ускорение . Переносное ускорение равно абсолютному ускорению , где R – расстояние от тела до оси вращения, знак «минус» означает, что  и  имеют противоположные направления. Используя определение силы инерции, получим следующее выражение для силы инерции, действующей на тело, которое покоится во вращающейся системе координат:

.

Эта сила инерции называется центробежной силой инерции. Она различна в разных точках вращающейся системы отсчета.

Рис. 5.5

Для примера рассмотрим диск, вращающийся с угловой скоростью w вокруг перпендикулярной к нему оси. Пусть вместе с диском вращается надетый на стержень шарик, прикрепленный к центру диска пружиной (рис. 5.5). Шарик занимает на диске такое положение, при котором сила упругости пружины сообщает ему нормальное ускорение: . Относительно системы отсчета, связанной с диском, шарик покоится, так как кроме силы упругости со стороны пружины на шарик действует центробежная сила инерции , направленная вдоль радиуса от центра диска.

Рис. 5.6

Из-за вращения Земли система отсчета, связанная с Землей, не является инерциальной. Если рассматривать движения тел в этой системе, то нужно вводить центробежную силу инерции во всех точках поверхности Земли кроме полюсов, , где r – расстояние от поверхности Земли до оси вращения, а w – угловая скорость вращения Земли вокруг ее оси. Эта сила перпендикулярна к оси вращения и составляет с силой тяжести некоторый угол, зависящий от географической широты местности (рис. 5.6). Действие сил инерции приводит к тому, что вес тела всюду, кроме полюсов, несколько меньше силы тяжести.

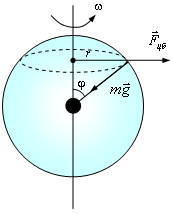
Неинерциальность земной системы отсчета проявляется и в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения. Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно .

Пример

Рисунок взят с сайта http://www.sppclub.ru

В аттракционе «Гигантские шаги» на каждого участника в системе отсчета, связанной с самим участником, действуют сила тяжести, сила натяжения каната и центробежная сила инерции. Эти силы уравновешивают друг друга. Система отсчета, связанная с Землей, является инерциальной для данного движения. В этой системе отсчета каждый участник движется по окружности под действием равнодействующей сил тяжести и натяжения каната