4.4. Кинетическая энергия вращательного движения твердого тела

Рассмотрим твердое тело, вращающееся с угловой скоростью  вокруг неподвижной оси. Будем рассматривать это тело как совокупность материальных точек с массами , через  обозначим расстояние от i-й материальной точки до оси вращения, тогда линейная скорость этой точки будет . Кинетическая энергия этой точки равна

.

Кинетическая энергия вращающегося тела складывается из кинетических энергий отдельных материальных точек, составляющих это тело:

.

Сумма в правой части этого соотношения  представляет собой момент инерции тела относительно оси вращения. Таким образом, кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна

.

5. Неинерциальные системы отсчета

5.1. Неинерциальные системы отсчета

Хотя существует бесконечное множество инерциальных систем отсчета, есть принципиально иной класс систем отсчета, называемых неинерциальными. В них скорость частицы изменяется без воздействия на нее других тел или частиц. Например, пронаблюдаем с помощью видеокамеры за камнем, движущимся по льду равномерно и прямолинейно. Если изображение формируется камерой, движущейся вдоль ледяного поля с ускорением, то, глядя на экран, мы увидим, что камень движется с ускорением.

Основные положения классической механики, сформулированные Ньютоном, выполняются только для описания движения в инерциальных системах отсчета. Как проверить, является ли данная система инерциальной? Для этого нужно рассмотреть простейший вид движения относительно этой системы и проверить, выполняется ли второй закон Ньютона.

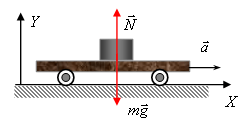
Рис. 5.1. Тело, лежащее на гладкой поверхности тележки, движущейся с ускорением, будет скользить в направлении, противоположном движению тележки

Рассмотрим для примера систему отсчета, связанную с тележкой, движущейся с ускорением . Пусть на абсолютно гладкой поверхности тележки стоят какие-либо предметы, которые могут скользить по ней без трения. В этом случае предметы не остаются неподвижными, а движутся в сторону, противоположную движению тележки с ускорением . Применим к описанию их движения второй закон Ньютона (рис. 5.1). Направим ось X по движению тележки, а ось Y перпендикулярно к ее поверхности. Рассмотрим силы, действующие на предмет. Вдоль оси Y действует сила притяжения к Земле  и сила реакции  со стороны тележки, которые равны по величине и противоположны по направлению. Следовательно,  и . Вдоль оси X силы также не действуют, то есть , и , и ускорение предмета . Это противоречит наблюдению. Таким образом, второй закон Ньютона в системе отсчета, связанной с движущейся тележкой, не выполняется.

Системы отсчета, связанные с телами, движущимися с ускорением по отношению к инерциальным системам, называют неинерциальными. Простейшими неинерциальными системами отсчета являются системы, движущиеся ускоренно прямолинейно, и вращающиеся системы.

5.2. Силы инерции

В инерциальных системах координат причиной ускорения являются силы. Сила является количественной мерой действия одного тела на другое, то есть сила всегда является результатом взаимодействия материальных тел. Кроме того, согласно третьему закону Ньютона силы взаимодействия тел равны по величине и противоположны по направлению. Сохранить оба эти положения невозможно при рассмотрении движения тел относительно неинерциальных систем.

При построении теории движения в неинерциальных системах можно было бы принять, что ускорения вызываются не только силами, но и некоторыми другими факторами, которые ничего общего с силами не имеют. Однако исторически был принят другой путь. Чтобы сохранить второй закон Ньютона для неинерциальных систем, было принято эти другие факторы считать силами, которые находятся с ускорениями в таких же соотношениях, как и обычные силы. Эти силы были названы силами инерции. Появление сил инерции не обусловлено действием каких-либо определенных тел. Таким образом, предполагается, что в неинерциальных системах ускорения вызываются только силами, но наряду с «обычными» силами взаимодействия существуют еще силы инерции. Необходимость введения сил инерции обусловлена только ускорением движения неинерциальной системы отсчета относительно инерциальной системы отсчета и не связана с действием каких-либо определенных тел. Поэтому для сил инерции несправедлив третий закон Ньютона.

С учетом сил инерции второй закон Ньютона принимает вид , где . В этом выражении  – ускорение тела относительно неинерциальной системы отсчета, его называют относительным ускорением;  – ускорение тела относительно инерциальной системы, часто его называют абсолютным ускорением;  – силы, обусловленные действием других тел,  – силы инерции.