4.2. Закон сохранения момента импульса

Из уравнения вращательного движения тела вытекает закон сохранения момента импульса. Если при вращении твердого тела вокруг неподвижной оси момент внешних сил относительно этой оси равен нулю, то

.

Следовательно, в этом случае момент импульса остается постоянным: .

В общем случае закон сохранения момента импульса формулируется следующим образом: если момент внешних сил относительно неподвижной оси вращения равен нулю, то момент импульса относительно этой оси остается постоянным и в том случае, когда момент инерции изменяется. Однако при этом неизбежно изменение угловой скорости вращения, так как произведение момента инерции на угловую скорость должно оставаться неизменным. В частном случае полный момент импульса остается постоянным в замкнутой системе тел.

Пример

Пример 1        

Пример 2

Примером проявления закона сохранения момента импульса при вращении тела относительно неподвижной оси является изменение скорости вращения балерины или фигуриста при изменении положения рук. При этом используется свойство угловой скорости изменяться за счет действия внутренних сил.На балерину действуют сила тяжести и сила реакции опоры, которые компенсируют друг друга. Момент силы трения относительно оси вращения очень мал, так как мала площадь опоры, а следовательно, малым будет и плечо силы трения. Таким образом, результирующий момент внешних сил относительно оси вращения можно положить равным нулю, а значит, должен сохраняться момент импульса относительно оси вращения, то есть Iω=const. Прижимая руки к телу или разводя их в стороны, балерина меняет момент инерции своего тела, что приводит к изменению угловой скорости

Чтобы увеличить количество оборотов, спортсменка группирует тело так, чтобы уменьшился момент инерции относительно оси вращения. Это приводит к увеличению угловой скорости вращения

4.3. Механическое равновесие

Раздел механики, в котором изучаются условия равновесия тел, называется статикой. Из второго закона Ньютона следует, что, если векторная сумма всех сил, приложенных к телу, равна нулю, то тело сохраняет свою скорость неизменной. В частности, если начальная скорость равна нулю, тело остается в покое. Условие неизменности скорости тела можно записать в виде:

,

или в проекциях на оси координат:

.

Очевидно, что тело может покоиться только по отношению к одной определенной системе координат. В статике изучают условия равновесия тел именно в такой системе. Необходимое условие равновесия можно получить также, рассмотрев движение центра масс системы материальных точек. Внутренние силы не влияют на движение центра масс. Ускорение центра масс определяется векторной суммой внешних сил. Но если эта сумма равна нулю, то ускорение центра масс , а, следовательно, скорость центра масс . Если в начальный момент , то центр масс тела остается в покое.

Таким образом, первое условие равновесия тел формулируется следующим образом: скорость тела не изменяется, если сумма внешних сил, приложенных в каждой точке, равна нулю. Полученное условие покоя центра масс является необходимым (но недостаточным) условием равновесия твердого тела.

Пример

Плавающий айсберг находится в состоянии равновесия, так как действующие на него силы тяжести и сила Архимеда равны по величине и противоположны по направлению, то есть выполняется условие

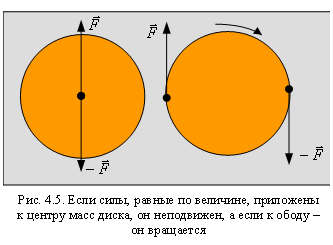
Может быть так, что все силы, действующие на тело, уравновешены, тем не менее, тело будет ускоряться. Например, если приложить две равных и противоположно направленных силы (их называют парой сил) к центру масс колеса, то колесо будет покоиться, если его начальная скорость была равна нулю. Если же эти силы приложить к разным точкам, то колесо начнет вращаться (рис. 4.5). Это объясняется тем, что тело находится в равновесии, когда сумма всех сил равна нулю в каждой точке тела. Но если сумма внешних сил равна нулю, а сумма всех сил, приложенных к каждому элементу тела, не равна нулю, то тело не будет находиться в равновесии, возможно (как в рассмотренном примере) вращательное движение. Таким образом, если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.

Чтобы получить второе условие равновесия, воспользуемся уравнением вращательного движения , где  – сумма моментов внешних сил относительно оси вращения. Когда , то и b = 0, а значит, угловая скорость тела не меняется . Если в начальный момент w = 0, то тело и в дальнейшем не будет вращаться. Следовательно, вторым условием механического равновесия является требование равенства нулю алгебраической суммы моментов всех внешних сил относительно оси вращения:

.

В общем случае произвольного числа внешних сил условия равновесия можно представить в следующем виде:

,

.

Эти условия необходимы и достаточны.

Пример

Кабина с туристами находится в равновесии, то есть не совершает ни поступательного, ни вращательного движения, так выполняются два условия равновесия:

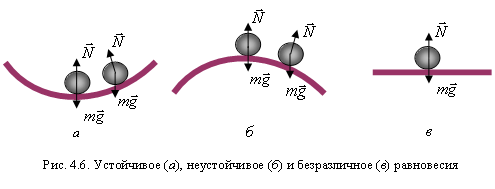
Равновесие бывает устойчивым, неустойчивым и безразличным. Равновесие является устойчивым, если при малых смещениях тела из положения равновесия действующие на него силы и моменты сил стремятся вернуть тело в положение равновесия (рис. 4.6а). Равновесие неустойчиво, если действующие силы при этом уводят тело еще дальше от положения равновесия (рис. 4.6б). Если при малых смещениях тела действующие силы по-прежнему уравновешиваются, то равновесие безразличное (рис. 4.6в). Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия. Шар, находящийся в верхней точке сферического выступа, – пример неустойчивого равновесия. Наконец, шар на дне сферического углубления находится в состоянии устойчивого равновесия.

Интересным примером равновесия тела на опоре является падающая башня в итальянском городе Пиза, которую по преданию использовал Галилей при изучении законов свободного падения тел. Башня имеет форму цилиндра радиусом 7 м. Вершина башни отклонена от вертикали на 4,5 м.

Пизанская башня получила известность благодаря тому, что она сильно наклонена. Башня «падает». Высота башни составляет 55,86 метров от земли на самой низкой стороне и 56,70 метров на самой высокой стороне. Её вес оценивается в 14700 тонн. Текущий наклон составляет около 5,5°. Вертикальная линия, проведенная через центр масс башни, пересекает основание приблизительно в 2,3 м от его центра. Таким образом, башня находится в состоянии равновесия. Равновесие нарушится и башня упадет, когда отклонение ее вершины от вертикали достигнет 14 м. По-видимому, это произойдет очень нескоро.

Полагали, что кривизна башни задумана зодчими изначально – ради демонстрации своего незаурядного умения. Но куда более вероятно другое: архитекторы знали, что строят на крайне ненадежном фундаменте, и потому заложили в конструкцию возможность легкого отклонения.

Когда возникла реальная угроза обрушения башни, за нее взялись современные инженеры. Ее затянули в стальной корсет из 18 тросов, фундамент утяжелили свинцовыми блоками и параллельно укрепили грунт, закачивая под землю бетон. С помощью всех этих мер удалось уменьшить угол наклона падающей башни на полградуса. Специалисты говорят, что теперь она сможет простоять еще как минимум 300 лет. С точки зрения физики принятые меры означают, что условия равновесия башни стали более надежными.

Для тела, имеющего неподвижную ось вращения, возможны все три вида равновесия. Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым (рис. 4.7а). Если же центр масс расположен выше оси – состояние равновесия неустойчиво (рис. 4.7б).

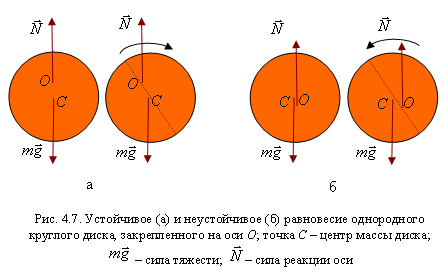
Особым случаем равновесия является равновесие тела на опоре. В этом случае упругая сила опоры приложена не к одной точке, а распределена по основанию тела. Тело находится в равновесии, если вертикальная линия, проведенная через центр масс тела, проходит через площадь опоры, то есть внутри контура, образованного линиями, соединяющими точки опоры. Если же эта линия не пересекает площадь опоры, то тело опрокидывается.

Пример