3.8. Потенциальная энергия частицы в поле

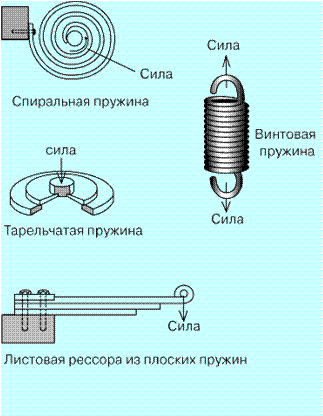
Различные виды механических пружин

Пружина – это устройство для временного накопления энергии за счет упругой деформации под действием нагрузки. С точки зрения классической физики, пружину можно рассматривать как устройство, накапливающее потенциальную энергию путём изменения расстояния между атомами эластичного материала. Накопленная энергия может использоваться для передачи движения, для осуществления контроля за движением или для поддержания определенного расстояния между деталями. Материалом пружины могут служить газ (воздух в автомобильных шинах), жидкость (масло в гидравлических амортизаторах), металл (стальные рессоры). Однако под «механическими пружинами» обычно понимают пружины из твердых материалов. Чаще всего пружины делают из стали, латуни и бронзы, но применяются также резина, пластики и специальные сплавы металлов.

Наиболее распространены витые, или винтовые, пружины. Бывают также спиральные, плоские, или пластинчатые, и тарельчатые пружины. Спиральная пружина в виде металлической ленты, свернутой в плоскую спираль, чаще всего применяется в часах в качестве заводной или волоска. Из плоских пружин, скрепленных на одном или обоих концах, состоит листовая рессора, часто применяемая в автомобильных подвесках. Тарельчатая пружина представляет собой металлический диск или набор дисков. Одна сила прикладывается по окружности наибольшей тарелки, а другая, противоположная, – в центре.

Пружина внутри безмена, на котором биолог взвешивает морского осетра, деформируется в соответствии с законом Гука. Потенциальная энергия упруго деформированной пружины при этом возрастает по закону , где  – изменение длины пружины.  В конструкции бельевой прищепки использована оригинальная пружина, изготовленная из полоски металла. Запасенная при сжатии пружины потенциальная энергия упругой деформации после освобождения пружины переходит в кинетическую энергию движения зажимающих концов прищепки. 

Материалы взяты с сайта http://www.krugosvet.ru

То обстоятельство, что работа потенциальных сил в случае стационарного поля сил зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии. Представим себе стационарное поле потенциальных сил, в котором мы перемещаем частицу из разных точек  в некоторую фиксированную точку О. Так как работа сил поля не зависит от формы траектории, то остается зависимость ее только от положения точки  (при фиксированной точке О). А это значит, что данная работа будет зависеть только от радиус-вектора точки .

.

(3.9)

Функцию  называют потенциальной энергией частицы в данном поле.

Рис. 3.11

Найдем работу сил поля при перемещении частицы из точки 1 в точку 2 (рис.3.11). Так как работа не зависит от формы траектории, то выберем траекторию, проходящую через точку О. Тогда работа на пути 1О2 может быть представлена как . Учитывая соотношение (3.9), эту работу можно записать в следующем виде:

.

(3.10)

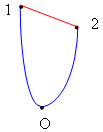
Выражение, стоящее справа, – убыль потенциальной энергии, то есть разность потенциальной энергии частицы в начальном и конечном положении. Таким образом, работа потенциальных сил поля при перемещении частицы из положения 1 в положение 2 равна убыли потенциальной энергии частицы в данном поле. Следует отметить: потенциальную энергию следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, создающих силовое поле. При данном характере взаимодействия частицы с окружающими телами потенциальная энергия частицы зависит только от ее положения относительно этих тел.

Таким образом, физический смысл имеет не само значение потенциальной энергии, а разность потенциальных энергий в двух положениях частицы, поэтому можно положить потенциальную энергию в некоторой точке пространства равной любому заданному значению, например, нулю. Тогда во всех остальных точках ее значение будет определяться однозначно, то есть потенциальная энергия определяется с точностью до произвольной постоянной. Это обстоятельство, однако, совершенно несущественно, так как ни одно явление в природе или технике не определяется значением самой потенциальной энергии, во все формулы входит только разность значений энергии в двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает.

Соотношение (3.10) дает возможность найти выражение для  для любого стационарного поля потенциальных сил. Для этого нужно вычислить работу, совершаемую силами поля на любом пути между двумя точками и представить ее в виде убыли некоторой функции, которая и есть потенциальная энергия. Именно так и было сделано при вычислении работы в поле упругих сил и в поле силы тяжести. Из (3.7) видно, что потенциальная энергия в поле упругих сил , если принять потенциальную энергию недеформированной пружины равной нулю. Потенциальная энергия в поле силы тяжести , где  отсчитывается от уровня, на котором потенциальная энергия полагается равной нулю. Таким образом, значение потенциальной энергии зависит от характера действующих сил.

Подчеркнем еще раз, что понятие потенциальной энергии имеет смысл для таких систем, в которых силы взаимодействия потенциальны, то есть зависят от расстояния между телами или между частями одного тела. Соответственно и потенциальная энергия зависит от расстояния между телами, или их частями, например, от высоты тела над поверхностью Земли, от длины пружины. Так как расстояния между двумя точками не зависят от выбора системы отсчета, то потенциальная энергия одинакова во всех системах отсчета.

Пример