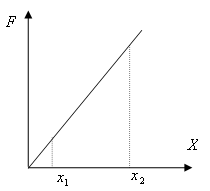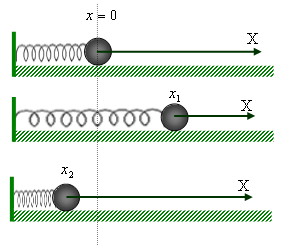
3.6. Примеры на вычисление работы
Рассмотрим несколько примеров на вычисление работы. При этом будем использовать явное выражение для сил взаимодействия между телами.
Работа упругой силы. Пусть тело
движется вдоль оси x под действием
упругой силы
.
Знак минус означает, что сила упругости
направлена к положению равновесия тела.
Пусть тело под действием этой силы
переместилось из точки с координатой
в
точку с координатой
(рис. 3.7).
Найдем работу силы
.
Как было показано ранее, работу можно
определить графическим методом: численно
она равна площади под кривой, описывающей
зависимость силы от координаты. В
рассматриваемом случае это площадь
трапеции, с основаниями, равными
и
,
и высотой, равной
(рис. 3.8).
Следовательно,
|
|
(3.7) |
.
Рис. 3.7 |
Рис. 3.8 |
Таким образом, работа силы упругости зависит только от величины деформации пружины, определяемой начальной и конечной длиной пружины. От формы траектории, по которой движется тело, работа не зависит. Действительно, при перемещении тела перпендикулярно оси пружины, когда ее длина не меняется, работа равна нулю, так как при этом сила перпендикулярна перемещению.
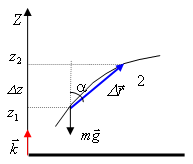
Рис. 3.9 |
,
где
–
орт вертикальной оси
,
положительное направление которой
выбрано вверх. Элементарная работа силы
тяжести на перемещении
будет
равна
.
Так как
,
то
.
Работа же этой силы на всем перемещении
от точки 1 до точки 2 равна
|
|
(3.8) |
.
При движении тела вверх сила тяжести совершает отрицательную работу. Если тело движется вниз, работа положительная. Работой силы, действующей на Землю со стороны тела, можно пренебречь, так как перемещение Земли ничтожно мало из-за ее огромной массы.
Итак, работу силы тяжести можно представить в виде разности двух значений величины, зависящей от взаимного расположения тела и Земли. Из (3.8) видно, что работа силы тяжести зависит только от изменения координаты тела относительно поверхности Земли, но не зависит от перемещения его в горизонтальном направлении.
Рассмотренные нами силы интересны в том отношении, что их работа, как видно из соотношений (3.7) – (3.8), не зависит от формы траектории между точками 1 и 2, а зависит только от положения этих точек. Этот результат оказывается справедливым не только для рассмотренных сил тяжести и упругости, но и для любых других сил, зависящих от расстояний между взаимодействующими телами, но не зависящих от их скоростей. Это весьма важная особенность данных сил присуща, однако, не всем силам. Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы траектории между ними.
3.7. Потенциальные и непотенциальные силы
Если в каждой точке пространства на помещенную туда частицу действует сила, то говорят, что частица находится в поле сил. Так, например, частица может находиться в поле сил тяжести, в поле упругих сил, в поле сил сопротивления (в потоке жидкости, газе).
Поле сил, остающееся постоянным во времени, называется стационарным. В стационарном силовом поле сила, действующая на частицу, зависит только от ее положения. Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от траектории, по которой перемещается частица из начального положения в конечное. Вместе с тем, имеются стационарные силовые поля, в которых работа, совершаемая над частицами силами поля, не зависит от формы траектории между точками 1 и 2. Силы, обладающие таким свойством, называются потенциальными или консервативными, а соответствующее поле сил – потенциальным полем. Примером потенциальных сил являются упругие силы, сила тяжести.
Рис. 3.10 |
и
(рис. 3.10).
Тогда работа на замкнутом контуре
.
Нетрудно сообразить, что
.
А так как в нашем случае работа не зависит
от формы траектории, то в результате и
оказывается, что работа сил при движении
частицы на произвольной замкнутой
траектории действительно равна нулю.
На этом основании можно утверждать, что потенциальным называется поле, в котором работа сил по замкнутому контуру равна нулю. С другой стороны, очевидно, – чтобы поле было потенциальным, нужно, чтобы работа сил поля на любом замкнутом контуре была равна нулю.
Все силы, не являющиеся потенциальными, называются непотенциальными или диссипативными. К числу непотенциальных сил относятся, например, силы трения и сопротивления. Работа этих сил зависит от формы траектории между начальным и конечным положениями частицы (и не равна нулю при перемещении вдоль замкнутого контура).