3.4. Энергия

Наблюдения показывают, что при определенных условиях любым телом может быть совершена работа. Например, сила упругости, действующая со стороны сжатой или растянутой пружины на прикрепленное к ней тело, перемещает его и при этом совершает механическую работу. Может совершать работу и любое движущееся тело. Сталкиваясь с другим телом, оно действует на него силой и может вызвать перемещение этого тела или его деформацию. При этом тоже совершается механическая работа. Про тела, которые могут совершать работу, говорят, что они обладают энергией.

Совершая механическую работу, тело или система тел переходят из одного состояния в другое. При этом их энергия уменьшается. Деформированная пружина распрямляется, движущийся груз останавливается, то есть при совершении работы энергия постепенно расходуется. Для того чтобы тело или система тел вновь приобрели способность совершать энергию, необходимо изменить их состояние: деформировать пружину, поднять тело вверх, то есть совершить над системой положительную работу.

Таким образом, энергия в механике – это величина, определяемая состоянием системы, то есть положением тел и их скоростями.

3.5. Кинетическая энергия

Определим, как энергия тела или системы тел зависит от их скоростей. Используя уравнение движения , можно от величины, характеризующей действие силы, перейти к некоторой величине, характеризующей состояние материальной точки или системы материальных точек. Элементарная работа:

,

(3.5)

где  – приращение вектора скорости на перемещении . Так как точка совершает малое перемещение, то можно положить . Тогда (3.5) можно записать следующим образом:

.

Полная работа силы  при перемещении материальной точки из начального положения 1 в конечное положение 2 будет равна

,

(3.6)

где  – начальная, а  – конечная скорости частицы на перемещении . Поскольку конечная скорость частицы на каждом элементарном участке совпадает с начальной скоростью на следующем элементарном участке, то (3.6) запишется следующим образом:

,

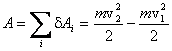где  – начальная, а  – конечная скорости частицы.

Следовательно, работа силы, действующей на материальную точку, идет на приращение некоторой величины, характеризующей состояние точки. Величина

называется кинетической энергией материальной точки. С помощью этого понятия полученный результат может быть записан в виде:

,

то есть работа всех сил при перемещении материальной точки равна приращению кинетической энергии этой точки. Энергия измеряется в тех же единицах, что и работа.

Рис. 3.4. Энергия, переданная кеглям шаром, зависит от его массы Рис.3.5. Разрушения, производимые ураганом, зависят от скорости ветра Рис. 3.6. Кинетическая энергия тела зависит от выбора системы отсчета

Таким образом, кинетическая энергия зависит от массы тела и скорости его движения. Например, чем больше будет масса шара при игре в боулинг, тем больше энергии он передаст кеглям при ударе, тем дальше они разлетятся (рис. 3.4). Чем больше скорость ветра при урагане, тем большие разрушения он может произвести (рис. 3.5).

Полученный результат без труда обобщается на систему материальных точек. Для i-й материальной точки системы приращение кинетической энергии равно работе всех сил, действующих на нее: . Поэтому работу А, которую совершают все силы, действующие на все точки системы при изменении ее состояния, можно записать:

или

,

где  – суммарная кинетическая энергия всей системы, то есть кинетическая энергия – величина аддитивная: кинетическая энергия системы частиц равна сумме кинетических энергий отдельных частей системы, независимо от того, взаимодействуют они между собой или нет.

Итак, приращение кинетической энергии системы материальных точек равно работе, которую совершают все силы, действующие на все частицы системы. Если работа положительна, кинетическая энергия увеличивается, а при отрицательной работе – уменьшается. При этом никаких предположений о характере сил взаимодействия частей системы между собой и с внешними телами не делалось. Это могут быть силы тяготения, силы упругости, силы трения и т.д.

Значение кинетической энергии, как и значение скорости, зависит от системы отсчета. С точки зрения различных наблюдателей кинетическая энергия одного и того же тела может быть различной. Например, с точки зрения наблюдателя, стоящего на горе, мотоциклист движется и, следовательно, обладает кинетической энергией, а кинетическая энергия горы равна нулю (рис. 3.6). Однако по отношению к мотоциклисту гора обладает кинетической энергией, так как стремительно движется мимо мотоциклиста.

Движущееся тело способно оказывать силовое воздействие на другие тела, и вы такие явления, бесспорно, наблюдали. Движущийся с большой скоростью мотоциклист, столкнувшись с препятствием, может его деформировать или разрушить, летящая стрела, врезаясь в мишень, оказывает силовое воздействие на ее волокна и раздвигает их.
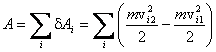