2.7. Второй закон ньютона для системы материальных точек. Закон сохранения импульса
Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно разделить на внутренние и внешние. Внутренними называются силы, с которыми на данное тело воздействуют остальные тела системы; внешними – силы, обусловленные воздействием тел, не принадлежащих системе. В случае если внешние силы отсутствуют, система называется замкнутой или изолированной.
Во Вселенной не может быть полностью изолированных систем, поскольку все тела взаимодействуют между собой. Однако при определенных условиях можно тело считать в достаточной степени изолированным. Например, материальное тело в некоторой области космического пространства, достаточно удаленной от массивных космических тел, ведет себя как изолированная система. В других случаях движение системы в определенных направлениях можно рассматривать как движение замкнутой системы, хотя в целом система таковой не является.
Третий закон Ньютона мы сформулировали
для замкнутой системы, состоящей из
двух материальных точек. Постулируем
теперь его справедливость для системы
из произвольного числа материальных
точек. Пусть
–
сила, с которой k-я точка системы действует
на i-ю, а
–
сила, с которой i-я точка действует на
k-ю. Третий закон Ньютона утверждает,
что обе эти силы направлены вдоль прямой,
соединяющей взаимодействующие точки,
причем
.
Это соотношение позволяет выполнить переход от механики отдельной материальной точки к механике системы материальных точек.
Пусть в системе из N взаимодействующих
частиц кроме внутренних сил
на
-ю
частицу действуют внешние силы,
результирующая которых равна
.
Запишем уравнение движение для каждой
из N частиц, входящих в систему:
Сложим правые и левые части этих
уравнений. Так как
,
то
.
Заметим, что импульс системы материальных точек является величиной аддитивной, то есть импульс системы материальных точек равен сумме импульсов отдельных точек, входящих в систему, независимо от того, взаимодействуют они между собой или нет:
,
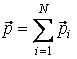где
–
импульс
-й
частицы. Тогда
|
. |
(2.9) |
Согласно полученному уравнению, импульс системы материальных точек может меняться только под действием внешних сил. Внутренние силы исключаются третьим законом Ньютона, поэтому внутренние силы не могут изменить импульс системы. Уравнение (2.9) является обобщением уравнения движения для одной материальной точки.
Таким образом, производная по времени от импульса системы материальных точек равна геометрической сумме всех внешних сил, действующих на систему.
2.8. Теорема о движении центра масс системы материальных точек
В любой системе частиц имеется одна
замечательная точка, называемая центром
масс, которая обладает рядом интересных
и важных свойств. Ее положение относительно
начала данной системы координат
характеризуется радиус-вектором
,
определяемым как
|
|
(2.10) |
,
где
–
масса и радиус-вектор
-й
частицы,
–
масса всей системы,
–
полное число частиц в системе. Если
взять производную по времени от обеих
частей уравнения и умножить обе части
на
,
то получится:
или
,
где
–
скорость движения центра масс системы.
Таким образом, импульс системы материальных
точек равен произведению массы системы
на скорость ее центра масс:
.
Подставив это выражение в (2.9), получим:
|
|
(2.11) |
.Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Этот результат называется теоремой о движении центра масс системы материальных точек. Уравнение (2.11) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на систему материальных точек: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы.
Если система замкнута, то
и
уравнение (2.11) переходит в
,
следовательно,
.
Таким образом, центр масс замкнутой
системы движется прямолинейно и
равномерно или покоится.
Примеры
Пример 1
Пример 2
В безвоздушном пространстве снаряд, выпущенный из пушки под некоторым углом к горизонту, будет двигаться по параболе под действием силы тяжести. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки под действием внутренних сил будут разлетаться в разные стороны. Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было. Действительно, результирующая внешняя сила, действующая на продукты распада, равна силе тяжести, действовавшей на неразорвавшийся снаряд.
|
При взрыве праздничной ракеты центр масс продуктов распада в течение некоторого времени продолжает двигаться по траектории, по которой двигалась бы ракета, если бы взрыва не произошло |
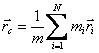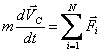