1) , Тогда и ;

2) , Тогда и .

В первом случае интерференция отсутствует, то есть суммарная интенсивность равна сумме интенсивностей волн, испускаемых каждым источником. Во втором имеет место интерференция, поскольку суммарная интенсивность не равна сумме интенсивностей волн, испускаемых каждым источником. Таким образом, необходимым условием интерференции является неравенство нулю интерференционного члена, .

Заметим, что если векторы  и  взаимно перпендикулярны, то , и интерференция не наблюдается. Поэтому можно утверждать, что интерференция наблюдается только для волн, в которых векторы напряженности электрического поля параллельны друг другу.

Можно показать, что интерференционный член равен нулю, если разность фаз складываемых колебаний хаотически изменяется за время наблюдения. Следовательно, необходимое условие интерференции можно сформулировать так: для возникновения интерференции необходимо, чтобы разность фаз складываемых колебаний сохраняла свое значение за время усреднения. Очевидно, что два любых гармонических колебания одинаковой частоты являются когерентными. Они порождают монохроматические волны, бесконечные в пространстве и во времени.

Таким образом, для наблюдения интерференции необходимо постоянство во времени разности фаз складываемых колебаний, равенство частот интерферирующих волн, параллельность векторов  и  и независимость от времени амплитуд световых волн.

В действительности идеально гармонические колебания неосуществимы, так как в реальных колебательных процессах амплитуда, частота и фаза колебаний непрерывно хаотически изменяются во времени. Если разность фаз двух колебаний изменяется очень медленно, то говорят, что колебания остаются когерентными в течение некоторого времени , пока их разность фаз не успела измениться на величину, сравнимую с . За это время волна распространится на расстояние , и колебания напряженности электрического поля волны в точках, удалённых друг от друга на расстояние  вдоль направления распространения волны, оказываются некогерентными. Расстояние, равное  вдоль направления распространения плоской волны, на котором случайные изменения фазы колебаний достигают величины, сравнимой с , называют длиной когерентности.

В оптике наиболее распространённым способом получения двух когерентных волн является расщепление волны, излучаемой одним источником, на две волны, распространяющиеся по разным путям, но, в конце концов, встречающиеся в одной точке, где и происходит их сложение. Если запаздывание одной волны по отношению к другой, связанное с разностью пройденных ими путей, меньше длины когерентности, то колебания в точке сложения будут когерентными, и будет наблюдаться явление интерференции. Когда разность оптических путей двух волн приближается к длине когерентности, интерференционная картина исчезает, и интенсивность в каждой точке пространства становится равной сумме интенсивностей двух волн.

2.2. Интерференция двух монохроматических волн

Рассмотрим идеализированный случай сложения двух монохроматических волн одинаковой частоты. Уравнение плоской монохроматической волны, распространяющейся в положительном направлении оси X, имеет вид:

.

Если амплитуда  и начальная фаза  одинаковы во все моменты времени во всем пространстве, то волна называется однородной. Строго монохроматические волны никогда не могут быть точно реализованы в действительности и представляют идеализацию реальных волновых процессов. Условия применимости этой идеализации в каждой конкретной задаче требуют специального рассмотрения.

П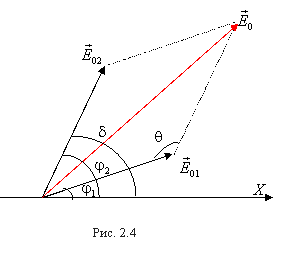 усть две плоские монохроматические волны одной частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:  и , где , .

Для сложения колебаний воспользуемся методом векторной диаграммы. Как видно из рис. 2.4, согласно теореме косинусов амплитуда результирующего колебания будет равна

.

Так как угол , то амплитуда результирующего колебания в данной точке определится выражением: , а интенсивность:

,

(2.4)

где   .

Если , , то интенсивность максимальна: , если , то интенсивность минимальна: .

Таким образом, при наложении двух монохроматических волн происходит устойчивое во времени перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. В тех точках пространства, для которых , результирующая интенсивность ; в точках, где , результирующая интенсивность .

Особенно отчетливо проявляется интерференция в том случае, когда интенсивности обеих интерферирующих волн одинаковы: . Тогда в максимумах , в минимумах же . Для некогерентных волн при том же условии получается всюду одинаковая интенсивность .

Определим положения максимумов и минимумов интерференционной картины в пространстве, рассмотрев два одинаковых синфазных монохроматических точечных источника  и , находящихся на расстоянии  друг от друга (рис. 2.5). Каждый из источников излучает сферическую волну, при этом, если , то можно считать амплитуды обеих волн в точке  одинаковыми и суммарная напряженность поля в этой точке  запишется:

,

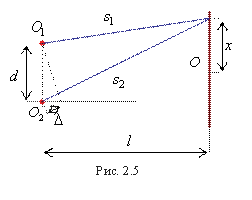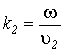г де , , и  в случае распространения волн в разных средах. Интенсивность результирующего колебания имеет вид

,

(2.5)

где .

В оптике вводится понятие оптического пути. Для среды с постоянным показателем преломления оптический путь равен . Величина  называется оптической разностью хода. Следовательно, разность фаз  может быть выражена через оптическую разность хода :

,

(2.6)

где ;  – длина волны в вакууме.

Таким образом, условия максимума и минимума определяются следующим образом:

, ,

(2.7)

, .

(2.8)

Если волны распространяются в средах с одинаковым показателем преломления, то поверхность равных фаз, соответствующих постоянной интенсивности складывающихся волн, определяется уравнением . На экране, параллельном линии источников , интерференционные полосы будут гиперболами. При этом в небольшой центральной части экрана интерференционная картина состоит из равноотстоящих почти параллельных светлых и темных полос. Найдем положение этих полос относительно точки  на экране. Из рис. 2.5 видно, что

, , .

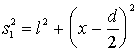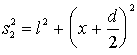Для получения различимой интерференционной картины расстояние между источниками  должно быть значительно меньше расстояния до экрана , . Расстояние , в пределах которого наблюдаются интерференционные полосы, также должно быть значительно меньше , . При этих условиях можно положить . Тогда . Если оба луча распространяются в одной среде, то, умножив  на показатель преломления этой среды , получим оптическую разность хода:

.

(2.9)

Подставляя это значение в условие для максимума интенсивности (2.7), получим, что максимумы интенсивности будут наблюдаться при значениях , равных

,

(2.10)

где  – длина волны в среде, заполняющей пространство между источниками и экраном. Подставив значение (2.9) в (2.8), получим координаты минимумов интенсивности

.

(2.11)

Расстояние между двумя соседними минимумами или двумя соседними максимумами будут одинаковыми и равными

.

(2.12)

Величина  называется шириной интерференционной полосы. Из формулы (2.12) видно, что ширина полосы растет с уменьшением расстояния между источниками. При расстоянии между источниками , сравнимом с , ширина полосы будет порядка l, и отдельные интерференционные полосы для электромагнитных волн оптического диапазона совершенно неразличимы. Поэтому для того, чтобы интерференционная картина была достаточно отчетливой, необходимо соблюдение условия .

Т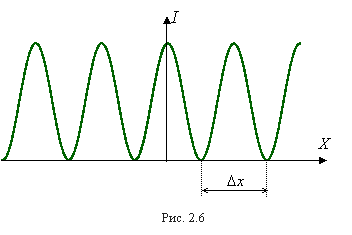 ак как разность фаз d пропорциональна оптической разности хода D, то в соответствии с (2.6) d растет пропорционально . Следовательно, как видно из (2.5), интенсивность изменяется вдоль экрана по закону квадрата косинуса. Для монохроматического света зависимость I от х имеет вид, представленный на рис. 2.6.

Отметим, что поскольку среднее значение , то среднее значение интенсивности на экране в интерференционной картине согласно формуле (2.5) равно удвоенной интенсивности от одного источника. Это значит, что при интерференции происходит только перераспределение энергии в пространстве, а полный поток энергии остается неизменным.

В действительности это условие приближенное и выполняется тем точнее, чем больше отношение . В противном случае, при , то есть когда расстояние между источниками много меньше длины волны, во всех точках пространства от обоих источников происходит сложение колебаний с практически одинаковыми фазами. Это значит, что повсюду интенсивности результирующих колебаний, а вместе с тем и полный поток энергии почти в четыре раза больше, чем при одном источнике. Однако это не противоречит закону сохранения энергии, так как близко лежащие источники, взаимодействуя через создаваемое ими поле излучения, вместе излучают больше энергии, чем в том случае, когда они находятся далеко друг от друга. Так для радиоволн, излучаемых близко расположенными антеннами, увеличение полного потока энергии происходит за счет работы генератора, поддерживающего неизменные амплитуды колебаний в антеннах.
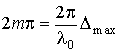
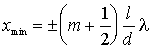