6.3. Линзы. Построение изображений в тонкой линзе. Формула линзы

Рис. 6.25

Преломление на сферической поверхности. Когда луч падает на сферическую границу раздела двух сред, построение отраженного и преломленного лучей производится следующим образом: строится плоскость касания в точке падения луча на сферическую поверхность и восстанавливается нормаль к этой плоскости в точке падения (рис. 6.25). Далее преломленный луч проводится в соответствии с законом преломления.

Рассмотрим преломление лучей на сферической поверхности прозрачной среды, такой, например, как одна из поверхностей линзы. Предположим, что источник света О находится в среде с показателем преломления , и лучи, исходящие из него, попадают в среду с показателем преломления  (рис. 6.26). Пусть R – радиус кривизны сферической границы раздела этих сред, С – центр сферы. Покажем, что все лучи, выходящие из точки О, соберутся в одной точке , являющейся изображением точки О, если ограничиться лучами, составляющими малый угол с осью и друг с другом. Такие лучи называются параксиальными. Геометрическая оптика – наука неточная, и одно из важнейших ее упрощений – приближение параксиальной оптики. Суть его заключается в том, что рассматриваются только те лучи, которые на своем пути незначительно отклоняются от оптической оси системы. Тогда угол между оптической осью и падающим лучом настолько мал, что можно считать, что .

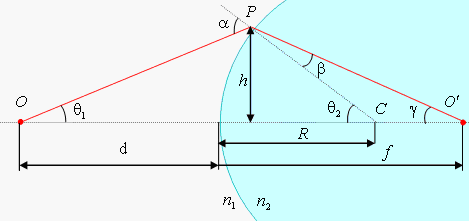
Рис. 6.26

Рассмотрим один из лучей, выходящих из точки О. Луч преломится в точке Р на границе раздела двух сред, согласно закону преломления:

.

Поскольку мы рассматриваем параксиальные лучи, то закон преломления можно записать следующим образом:

.

Из рис. 6.26 видно, что , следовательно,

.

(6.3)

Вследствие малости углов  можно считать, что , , . Подставляя значения углов в (6.3) и поделив все члены на h, получим

.	(6.4)

Рис.6.27

Из (6.4) видно, что при заданном расстоянии d от сферической поверхности до источника расстояние от сферической поверхности до изображения f не зависит от угла, который луч образует с осью. Следовательно, все параксиальные лучи сходятся в одной точке .

На рис. 6.26 лучи падают на выпуклую часть сферической поверхности. Но полученное соотношение (6.4) справедливо и для вогнутой поверхности. Это видно из рис. 6.27, если считать, что R и f являются отрицательными. Заметим, что в случае вогнутой поверхности изображение получается мнимым.

а)               б) Рис. 6.28. А) двояковыпуклая линза, б) двояковогнутая линза.

Тонкие линзы. Тонкие линзы являются наиболее важным и простым оптическим устройством. Упоминания об очках встречаются еще в рукописях XIII в. Тонкие линзы чаще всего бывают круглыми, и каждая из поверхностей представляет собой сегмент сферы. Ограничивающая линзу поверхность может быть выпуклой, вогнутой или плоской (рис. 6.28). Действие линз можно проанализировать, если применить результаты, полученные для преломляющей поверхности, к ограничивающим линзу поверхностям.

Рис. 6.29

Предварительно остановимся на некоторых общих свойствах линз. Прямая, проходящая через центры сферических поверхностей, ограничивающих линзу, называется главной оптической осью. Любая другая прямая, проходящая через оптический центр линзы, называется побочной оптической осью. Рассмотрим лучи, параллельные главной оптической оси двояковыпуклой линзы, изготовленной из прозрачного вещества, показатель преломления которого больше, чем показатель преломления воздуха. В этом случае, согласно закону преломления, на обеих поверхностях линзы каждый луч отклоняется от нормали к поверхности линзы в направлении оси линзы. Если на линзу падают лучи, параллельные главной оптической оси, то они соберутся в точке F, называемой фокальной точкой или главным фокусом линзы (рис. 6.29). Для линзы, ограниченной сферическими поверхностями, такое утверждение верно, если диаметр линзы мал по сравнению с радиусами кривизны поверхностей линзы. Линзы, удовлетворяющие такому условию, называются тонкими. Поскольку лучи от удаленного объекта можно считать параллельными, то можно утверждать, что фокальная точка служит точечным изображением находящегося на главной оси бесконечно удаленного объекта. Расстояние от фокальной точки до центра линзы называется фокусным расстоянием F. Для тонкой линзы фокусное расстояние можно отсчитывать от любой точки линзы, лежащей на главной оптической оси. Если параллельный главной оптической оси пучок лучей падает на линзу с другой стороны, то они соберутся в другом фокусе линзы. Можно показать, что, если показатель преломления среды, в которой находится линза, везде одинаков, фокусное расстояние, независимо от радиусов кривизны линзы, будет одинаковым с обеих сторон. Плоскость, проходящая, через главный фокус перпендикулярно главной оптической оси линзы, называется фокальной плоскостью.

Рис. 6.31

Если на линзу падает пучок лучей, параллельный какой-либо побочной оптической оси, то он сфокусируется в точке пересечения этой оси с фокальной плоскостью  (рис. 6.30). Эту точку называют побочным фокусом. Любые линзы, толщина которых в центре больше, чем по краям, будут сводить параллельные лучи в точку. Такие линзы называются собирающими. Линзы, которые в центре тоньше, чем по краям, называются рассеивающими. После прохождения через рассеивающую линзу лучи расходятся. Фокусом F рассеивающей линзы называется точка, в которой сходятся продолжения преломленных лучей (рис. 6.31). Расстояние от фокуса F до линзы, как и в случае собирающей линзы, называется фокусным расстоянием.

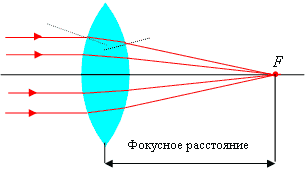
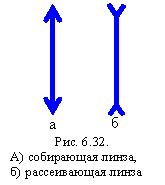
На оптических схемах тонкие линзы изображают в виде отрезков со стрелками на концах. В зависимости от направления стрелок, на схемах различают собирающие и рассеивающие линзы (рис. 6.32).

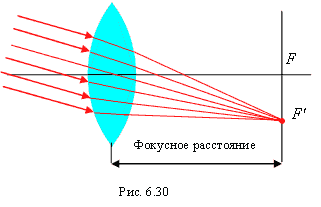
Изображение данного объекта тонкой линзой можно построить, начертив три луча, исходящие из каждой точки объекта (рис. 6.33). Один луч проведен параллельно главной оптической оси линзы. Преломившись в линзе, он пройдет через задний фокус. Второй луч проведен через передний фокус, после преломления он пойдет параллельно главной оптической оси. Третий луч проведен через центр линзы, где обе ее поверхности по существу параллельны друг другу, поэтому этот луч преломляться не будет. В действительности для нахождения изображения точки достаточно провести любые два из этих лучей. Изображения всех остальных точек можно найти аналогично. В рассмотренном случае преломленные лучи проходят через изображение. Такое изображение называется действительным.

Рис. 6.33

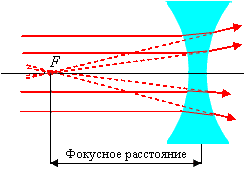
Рис. 6.34

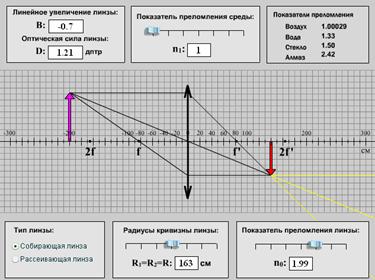
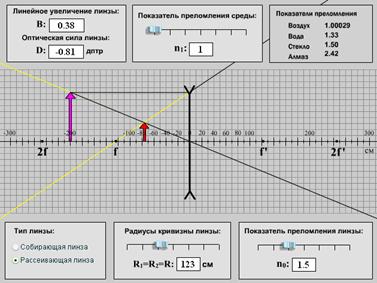
С помощью таких же лучей можно построить изображение, даваемое рассеивающей линзой (рис. 6.34). В этом случае луч, параллельный главной оптической оси, преломившись, пойдет так, что его продолжение пройдет через передний фокус линзы. Луч, идущий через центр линзы, не преломляется. Точка пересечения продолжений преломленных лучей и будет мнимым изображением рассматриваемой точки.

Формула линзы. Получим уравнение, связывающее расстояния от линзы до объекта и его изображения со свойствами и размерами тонкой линзы. Рассмотрим линзу, толщина которой в центре равна t (рис. 6.35). Лучи из точки О объекта проходят через линзу и фокусируются в точке I изображения. Будем считать лучи параксиальными. Для передней поверхности линзы уравнение (6.4) имеет вид

,

(6.5)

где  – радиус кривизны этой поверхности,  – показатель преломления среды, окружающей линзу,  – показатель преломления вещества линзы. Расстояния d и  (расстояние от передней поверхности линзы до изображения) измеряются от передней поверхности линзы. Для случая, изображенного на рис. 6.35, величина  отрицательна, так как в точке  находится мнимое изображение точки О.

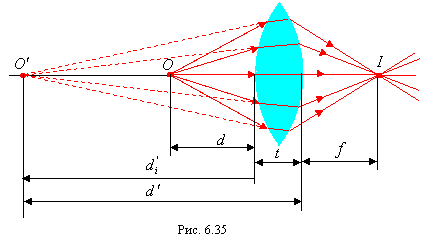
Применим уравнение (6.4) ко второй поверхности линзы. На эту поверхность падают лучи, которые как будто исходят из точки . Расстояние от этой точки до второй поверхности равно  (знак минус поставлен потому, что величина  отрицательна). Тогда уравнение (6.4) примет вид:

,

(6.6)

где  – радиус кривизны второй поверхности. В рассматриваемом случае  – отрицательная величина. Если толщина линзы мала, то есть , то, полагая  и исключая  из соотношений (6.5) и (6.6), получим

.

(6.7)

Это соотношение и требовалось получить. Оно связывает расстояния от линзы до объекта и изображения с радиусами кривизны передней и задней поверхности линзы и ее показателем преломления. Полученное соотношение справедливо только для тонких линз и параксиальных лучей. В (6.7) расстояние от линзы до изображения f не зависит от углов, которые лучи образуют с осью, именно поэтому все параксиальные лучи собираются после прохождения через линзу в одной точке.

Если объект удален на бесконечность, , то расстояние до изображения совпадает с фокусным расстоянием . Уравнение (6.7) при этом принимает вид:

.

(6.8)

Это уравнение связывает фокусное расстояние линзы с ее радиусами кривизны и показателями преломления вещества линзы и среды, в которой она находится. Как уже указывалось, радиус кривизны считается положительным, если свет падает на выпуклую поверхность, и отрицательным, если свет падает на вогнутую поверхность. Одна и та же линза может быть и рассеивающей, и собирающей, в зависимости от соотношения показателей преломления  и . Так, двояковыпуклая линза, для которой 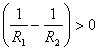, может стать рассеивающей, если . Если свет будет падать на линзу с противоположной стороны, радиусы кривизны в уравнении (6.8) поменяются ролями, но фокусное расстояние F останется прежним, то есть оба фокуса находятся на одинаковом расстоянии от линзы, если по обе стороны от линзы находится одна и та же среда. Если же по разные стороны от линзы расположены среды с различными показателями преломления слева , а справа , то переднее и заднее фокусные расстояния будут различными. Их отношение определится формулой:

.

Следует отметить, что в случае  центр линзы не будет оптическим центром: луч, проходящий через него, будет преломляться.

Чем сильнее линза изменяет направление лучей, тем меньшим получается ее фокусное расстояние. Поэтому оптическая сила линзы обратно пропорциональна ее фокусному расстоянию. Величина  называется оптической силой линзы и характеризует ее преломляющую способность:

.

(6.9)

Для собирающих линз , а для рассеивающих . Оптическая сила не зависит от направления хода лучей: слева направо или наоборот. Оптическая сила линзы измеряется в диоптриях. Одна диоптрия – это оптическая сила линзы, фокусное расстояние которой составляет 1 м.

Из уравнений (6.7) и (6.8) следует:

.

(6.10)

Эта формула называется формулой линзы. Она справедлива как для собирающих, так и для рассеивающих линз. При известном фокусном расстоянии линзы она позволяет легко вычислить расстояние до изображения при любом расстоянии до объекта, если придерживаться тех соглашений, которые были использованы при ее выводе:

• фокусное расстояние положительно для собирающих и отрицательно для рассеивающих линз;

• радиус кривизны считается положительным, если свет падает на выпуклую поверхность, и отрицательным, если свет падает на вогнутую поверхность;

• расстояние до объекта положительно, если свет падает на линзу со стороны объекта (это обычный случай, но при использовании комбинации линз ситуация может быть иной), и отрицательно в противном случае;

• расстояние до изображения положительно, если свет падает на противоположную сторону линзы; если свет падает с той же стороны, где находится изображение, то величина f отрицательна; другими словами, это означает, что расстояние от линзы до изображения положительно в случае действительного изображения и отрицательно в случае мнимого изображения.

Увеличение линзы. Линейным увеличением линзы называется отношение величины изображения предмета h к величине самого предмета H:

.

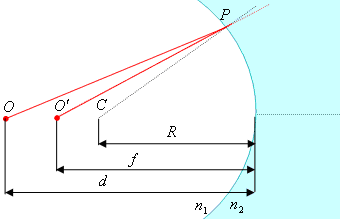
Из рис. 6.33 видно, что вследствие подобия треугольников:

.

В астрономии чаще применяют угловое увеличение, которое определяют как отношение угла, под которым видно изображение , к углу, под которым виден объект :

.
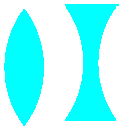
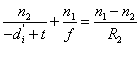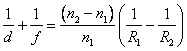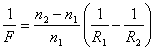