Это интересно! 6. Геометрическая оптика

6.1. Основные законы геометрической оптики

Длины световых волн, воспринимаемых глазом, очень малы, поэтому при решении многих задач оптики можно отвлечься от волновой природы света. Если размеры отверстий и препятствий велики по сравнению с длиной световой волны, то дифракционными явлениями можно пренебречь и считать, что свет распространяется вдоль лучей. Дифракция оказывается тем слабее, чем меньше длина волны. При этом описание явлений и анализ действия различных устройств сводится к рассмотрению геометрии хода световых лучей. Соответствующий раздел оптики называется геометрической оптикой. Геометрическая оптика, таким образом, соответствует предельному случаю малых длин волн: .

Геометрическая оптика широко используется в светотехнике и при рассмотрении действий многочисленных приборов и устройств – от лупы и очков до сложнейших оптических микроскопов и телескопов.

Основу геометрической оптики составляют четыре закона:

• закон независимости световых лучей;

• закон прямолинейного распространения света (в однородной среде);

• закон отражения света;

• закон преломления света (закон Снеллиуса).

Рис. 6.1

Закон независимости световых лучей. Опыт показывает, что световые пучки при пересечении, как правило, не возмущают друг друга, то есть лучи света распространяются независимо друг от друга. Это означает, что действие одного пучка не зависит от наличия других пучков (рис. 6.1). Согласно принципу суперпозиции суммарная интенсивность двух пучков в этом случае равна сумме интенсивностей каждого пучка в отсутствие другого (рис. 6.2). Нарушение этого закона приводит к явлению интерференции.

Рис. 6.2

Закон независимости световых лучей строго справедлив для вакуума. Для световых лучей в веществе закон независимости лучей выполняется точно при небольшой интенсивности света и нарушается при распространении в веществе света большой интенсивности, например, лазерного излучения.

Рис. 6.3

Закон прямолинейного распространения света. Геометрическая оптика рассматривает излучение как тонкие пучки света – лучи, распространяющиеся прямолинейно в однородной среде. Закон прямолинейного распространения света был установлен ещё в глубокой древности. Впервые он упоминается в сочинении по оптике Евклида, написанном 300 лет до н.э. Понятие прямой линии в геометрии значительным образом сформировалось именно в результате наблюдения оптических наблюдений.

Рис. 6.4

На рис. 6.3 изображен пучок лучей, идущих от фонаря, имеющего насадку с разноцветными фильтрами. Видно, что лучи разного цвета распространяются прямолинейно и независимо друг от друга. Прямолинейное распространение света можно наблюдать в солнечный день, когда лучи света, идущие через просветы в листве, прямыми линиями рассекают лес (рис. 6.4).

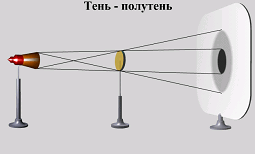
Прямолинейность световых лучей означает, что форма тени предмета при его освещении точечным источником соответствует геометрической проекции контура предмета с центром в источнике (рис. 6.5). При освещении предмета протяженным источником света края тени оказываются размытыми. В область между полной тенью и светом, в область полутени, попадают лучи не от всех точек источника (рис. 6.6).

Геометрическая оптика допускает искривление лучей света в оптически неоднородных средах.

Рис. 6.5

Рис. 6.6

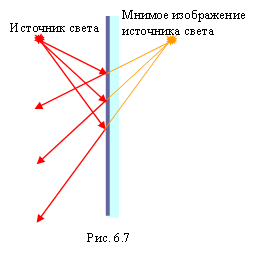
Закон отражения света. Мы видим источник света, если лучи, исходящие из него, попадают в глаз. Если тело не является источником света, то глаз может воспринимать лучи, отраженные поверхностью тела, на которое падают лучи от источника света.

Слово «отражение» ассоциируется у нас прежде всего с зеркалом. В повседневной жизни чаще всего используются плоские зеркала. В плоском зеркале мы видим изображения предметов, расположенных перед ним, которые в точности повторяют внешний вид этих предметов.

Угол между падающим лучом и перпендикуляром, восстановленным к отражающей поверхности в точке падения, в оптике принято называть углом падения. Угол между тем же перпендикуляром и отраженным лучом – углом отражения.

Закон отражения света гласит:

• падающий луч, отраженный луч и перпендикуляр к отражающей поверхности, восстановленный в точке падения, лежат в одной плоскости;

• угол падения равен углу отражения.

Рассмотрим изображение точечного источника в плоском зеркале. Для этого проведем от источника несколько лучей и построим соответствующие им отраженные лучи (рис. 6.7). Продолжения отраженных лучей пересекутся в одной точке за плоскостью зеркала. Эта точка и есть изображение источника. В действительности световые лучи не проходят сквозь зеркало. Нам только кажется, что свет исходит от изображения, поскольку наш мозг воспринимает попадающий в глаза свет как свет от источника, находящегося перед нами. Нам кажется, что лучи исходят из этой точки, хотя на самом деле источника света в ней нет. Подобное изображение принято называть мнимым. Источник света и его изображение расположены симметрично относительно зеркала.

Рис. 6.8

Пучок лучей, выходящих из точечного источника, называется гомоцентрическим. Гомоцентрический пучок лучей после отражения в плоском зеркале остается гомоцентрическим: продолжения отраженных лучей пересекаются за зеркалом в одной точке, являющейся мнимым изображением источника. При отражении от плоской зеркальной поверхности световых лучей, исходящих от некоторого предмета, возникает мнимое изображение предмета. Предмет и его мнимое изображение располагаются симметрично относительно зеркальной поверхности (рис. 6.8). Изображение предмета в плоском зеркале равно по размеру самому предмету. Мнимое изображение пространственного предмета в плоском зеркале отличается от самого предмета как правая система координат отличается от левой.

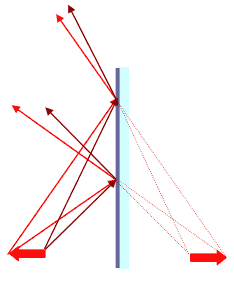
Если свет падает на шероховатую поверхность, то после отражения света он распространяется во всевозможных направлениях. Такое отражение называется рассеянным или диффузным.

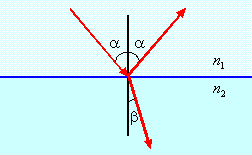
Закон преломления света (закон Снеллиуса). При падении света на границу раздела прозрачных сред с показателями преломления  и  часть света отражается, а часть проходит во вторую среду, изменяя направление распространения – преломляется. В отличие от закона отражения света, известного с глубокой древности, закон преломления света был сформулирован в XVII в.

Рис. 6.9

Преломление света связано с тем, что в разных средах свет распространяется с различной скоростью. Скорость распространения света в среде характеризует оптическую плотность данной среды: чем выше скорость света в данной среде, тем меньше ее оптическая плотность. Поскольку абсолютный показатель преломления среды , то чем больше показатель преломления среды, тем больше ее оптическая плотность.

Опыты по преломлению света позволили сформулировать закон преломления света следующим образом (рис. 6.9):

• падающий и преломленный лучи, а также перпендикуляр, восстановленный в точке падения, лежат в одной плоскости;

• отношение синуса угла падения к синусу угла преломления есть величина, постоянная для двух сред; углы падения и преломления связаны соотношением

.

(6.1)

Из (6.1) видно, что при переходе луча из среды с большим показателем преломления в среду с меньшим показателем преломления, или, как говорят, из оптически более плотной среды в оптически менее плотную угол преломления больше угла падения. При переходе из оптически менее плотной среды в оптически более плотную угол преломления меньше угла падения.

Рис. 6.10

Преломлением обусловлен целый ряд широко известных оптических иллюзий. Например, наблюдателю на берегу кажется, что у человека, зашедшего в воду по пояс, ноги стали короче. Это обусловлено тем, что лучи, исходящие от ступней, преломляются на поверхности воды, при этом угол преломления больше угла падения. Глаза же (и мозг) наблюдателя воспринимают эти лучи как прямолинейные, а значит, видят ступни ног на продолжении отраженного луча, то есть выше той точки, из которой они испущены. Вследствие преломления происходит кажущееся изменение формы предмета. Монета, погруженная в воду, кажется нам более крупной по сравнению с тем, когда она просто лежит на столе. Ложка в стакане с водой выглядит надломленной в том месте, где она входит в жидкость (рис. 6.10).

Принцип Ферма. В основу геометрической оптики вместо рассмотренных законов может быть положен принцип Ферма. Он утверждает, что свет распространяется по такому пути, для прохождения которого ему требуется экстремальное время, то есть время должно быть либо минимальным, либо максимальным, либо одинаковым для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными, то есть требующими для своего прохождения одинакового времени. Из принципа Ферма следуют три закона: закон прямолинейного распространения света, закон отражения и закон преломления света.

Действительно, в однородной среде свет должен распространяться прямолинейно, поскольку прямая – это кратчайшее расстояние между двумя точками, и, следовательно, время распространения в этом случае наименьшее.

Если же свет падает на границу раздела двух оптически различных сред, то есть на границу раздела сред с разными показателями преломления, то выполняются законы отражения и преломления света. Докажем закон отражения света.

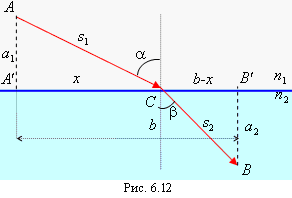
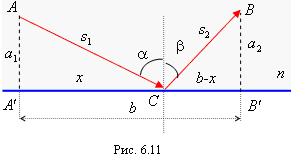
Пусть свет падает на границу раздела двух сред и отражается от границы раздела в точке С, положение которой нужно определить. Обозначим угол падения , а угол отражения , отрезок  (рис. 6.11). Оптическая длина пути, по которому распространяется луч, будет равна

.

Чтобы найти экстремум величины L, возьмем производную от L по x:

.

(6.2)

Так как , , то, подставив эти выражения в (6,2), получим

.

Следовательно, .

Пусть свет падает на границу раздела двух прозрачных диэлектриков с показателями преломления  и  (рис. 6.12). Найдем положение точки С, в которой должен преломиться луч, распространяясь от точки А к точке В, чтобы оптическая длина пути L была экстремальной. Оптическая длина пути, как видно из рис. 6.12, будет равна

.

Чтобы найти экстремум величины L, возьмем производную от L по x:

. 

Учитывая, что , , получим . Таким образом, получаем закон преломления, что и требовалось доказать.

Интенсивность отраженного и преломленного света. Законы геометрической оптики позволяют определить только направление световых лучей, но ничего не говорят об их интенсивности. Опыт показывает, что соотношение интенсивностей отраженного и преломленного лучей сильно зависит от угла падения. При нормальном падении света на поверхность, например, воды, энергия отраженного луча составляет всего 2 % от энергии падающего луча. Но при скользящем падении отражается почти все падающее излучение. Это и позволяет нам видеть зеркальные отражения прибрежных пейзажей в спокойной прозрачной воде (рис. 6.13).

Рис. 6.13