3.6. Дифракция Френеля от непрозрачного экрана

Пусть на пути света от точечного источника помещен непрозрачный экран, который перекрывает центральную часть волнового фронта (рис. 3.15). В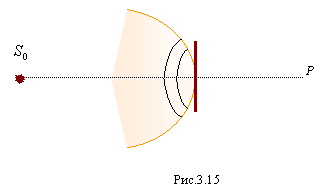 этом случае будет закрыта одна или несколько первых зон Френеля. Расчет интенсивности проводится точно так же, как и при полностью открытом волновом фронте, однако суммирование начинается с первой открытой зоны Френеля. Если закрыто  зон Френеля, то результирующая амплитуда в точке   , то есть равна половине амплитуды первой открытой зоны Френеля. Если размер экрана невелик, то есть он закрывает малое число зон, то действие первой открытой зоны практически не отличается от действия центральной зоны Френеля, и освещенность в точке  будет почти такой же, как в отсутствие экрана. Вследствие симметрии задачи, как и при дифракции на круглом отверстии, центральное светлое пятно будет окружено темными и светлыми кольцами.

Полученный результат на первый взгляд кажется абсурдным, потому что в обычных условиях за препятствием наблюдается минимум интенсивности. Это было использовано Пуассоном в 1818 г. для опровержения теории Френеля. В начале 1817 г. Парижская академия наук выдвинула на премию задачу о дифракции. Подразумевалось, что явление дифракции получит свое объяснение в рамках корпускулярной теории света. Из пяти членов комиссии трое (Пуассон, Био и Лаплас) были убежденными сторонниками корпускулярной теории света, и только Араго придерживался волновой. Пятый член комиссии, Гей-Люссак, не был компетентен в рассматриваемом вопросе, но был известен исключительной честностью.

В 1818 г. Френель представил в Академию в запечатанном конверте «Записку о теории дифракции». В этой записке он описал многочисленные опыты по дифракции, результаты которых объяснял, используя принцип Гюйгенса–Френеля, то есть на основе волновой теории. При обсуждении работы Пуассон заметил, что теория Френеля противоречит здравому смыслу: в самом центре тени, отбрасываемой небольшим диском, должно находиться светлое пятно.

Однако Араго доказал экспериментально существование светлого пятна в центре геометрической тени и показал, что выводы Пуассона соответствуют действительности и лишь подтверждают теорию Френеля. В результате работа Френеля получила заслуженную премию, а волновая теория – всеобщее признание. Светлое пятно в центре тени носит название пятна Араго–Пуассона или просто пятна Пуассона.

Рис. 3.16

Для того чтобы интенсивность в точке Р была достаточной для наблюдения, необходимо, чтобы экран перекрывал одну или небольшое число зон. На рис. 3.16 приведена дифракционная картина, которая наблюдается на экране, расположенном перпендикулярно прямой  для дифракции на круглом диске. В центре дифракционной картины всегда будет темное пятно (пятно Араго–Пуассона), окруженное светлыми и темными кольцами.

3.7. Дифракция Фраунгофера на одной щели

Наибольший практический интерес представляют дифракционные явления, наблюдаемые при падении на экран или отверстие в экране параллельного пучка света. В результате дифракции пучок утрачивает параллельность, то есть появляется свет, распространяющийся в направлениях, отличных от первоначального. Распределение его интенсивности на очень большом расстоянии от экрана соответствует дифракции Фраунгофера. Волны, возникающие в результате ограничения падающей плоской волны при прохождении сквозь отверстие на экране, называются дифрагировавшими, а нормали к их волновым поверхностям – дифрагировавшими лучами.

Дифрагировавшие лучи не существуют в рамках геометрической оптики. Возникновение дифрагировавших волн при прохождении через отверстие означает, что волна с ограниченной площадью поперечного сечения не может быть строго плоской.

Рис. 3.17

Рассмотрим дифракцию Фраунгофера на одной щели. Пусть на бесконечно длинную щель падает плоская световая волна (рис. 3.17). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы – экран. Фронт падающей волны, плоскость щели и экран параллельны друг другу.

Распределение интенсивности света при дифракции Фраунгофера можно найти с помощью принципа Гюйгенса–Френеля. Интенсивность в точке экрана Р обусловлена интерференцией вторичных волн, исходящих от всех элементарных участков щели. Причем эти волны распространяются в одном и том же направлении, характеризуемом углом j. Заметную интенсивность имеют при этом лишь волны, дифрагировавшие на малые углы.

Когда размеры отверстия велики по сравнению с длиной волны, напряженность поля на поверхности, совпадающей с плоскостью щели, можно считать такой же, какой она была в отсутствии экрана.

Разобьем открытую часть волновой поверхности на параллельные краям щели элементарные зоны шириной . Каждая такая зона становится источником вторичных волн. Вторичные волны, посылаемые этими зонами в направлении, определяемом углом j, соберутся в точке экрана Р. Каждая волна, испущенная элементарной зоной, создаст в точке Р колебание . Линза собирает в фокальной плоскости плоские волны. Поэтому амплитуда волны  не зависит от расстояния до точки наблюдения. Ограничившись рассмотрением малых углов j, можно считать, что коэффициент . Тогда амплитуда колебания, возбуждаемого зоной в любой точке экрана, будет зависеть только от площади зоны. Площадь зоны пропорциональна ее ширине . Следовательно, колебания  от каждой полоски имеют одинаковую амплитуду и отстают по фазе от колебания, создаваемого соседней полоской на одну и ту же величину , зависящую от угла дифракции .

Ч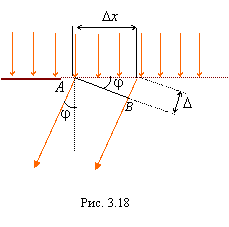 тобы найти значение , проведем плоскость АВ, перпендикулярную к направлению дифрагировавших лучей (рис. 3.18). Собирающая линза обладает свойством, называемым таутохронностью: если свет по двум разным путям распространяется за одно и то же время, то пути называются таутохронными, то есть оптические длины этих путей равны между собой. Условию таутохронизма удовлетворяют все пути лучей, проходящих через линзу. Следовательно, линза не вносит дополнительной разности хода для дифрагировавших волн. Таким образом, достаточно определить разность хода , возникающую на пути от плоскости щели до плоскости АВ. Величина  связана с разностью хода соотношением . Тогда, как видно из рис. 3.18, .

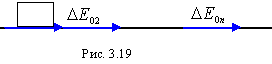
Задачу о дифракции Фраунгофера на одной щели можно решить графическим методом. При  разность фаз , и векторная диаграмма имеет вид прямой (рис. 3.19), при этом амплитуда колебания в центре экрана .

Е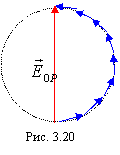 сли разность фаз между колебаниями от краев щели равна , то результирующая амплитуда колебаний в точке P представляет диаметр полуокружности, длина которой равна  (рис. 3.20). Следовательно, в этом случае , а интенсивность в таком направлении соответственно . Следующий максимум получается, когда строго последовательно мы обойдем полторы окружности. Тогда диаметр , интенсивность этого максимума , и т.д. Относительная интенсивность максимумов получается равной , то есть интенсивность максимумов быстро уменьшается.

Е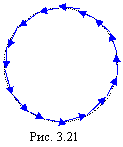 сли колебания от краев щели имеют разность фаз , то результирующая амплитуда равна нулю, так как ломаная линия в этом случае замыкается (рис. 3.21). Отсюда следует, что первый минимум получается при . Следовательно, первый минимум можно наблюдать под углом, для которого . Можно показать, что основная часть потока энергии за щелью сосредоточена в этих пределах изменения угла дифракции.

Результирующая амплитуда будет равна нулю и тогда, когда разность фаз от краев щели равна , где  – целое число. Цепочка векторов в этом случае замыкается после  оборотов. Следовательно, условие минимума интенсивности при дифракции Фраунгофера на одной щели имеет вид

,

(3.11)

где n принимает значения .

Рис. 3.22

Из формулы (3.11) видно, что , то есть дифракционная картина симметрична относительно центра линзы. График зависимости интенсивности от угла дифракции представлен на рис. 3.22. По оси абсцисс отложены значения , по оси ординат – интенсивность .

Количество минимумов интенсивности определяется отношением ширины щели  к длине волны . Модуль  не может превысить единицу, поэтому из условия минимума следует, что , откуда . При ширине щели, меньшей длины волны, минимумы вообще не возникают. В этом случае интенсивность света монотонно убывает от середины картины к ее краям.

Поскольку положение максимумов и минимумов зависит от длины волны , то дифракционная картина имеет описанный вид только для монохроматических волн. В случае белого света мы имеем совокупность соответствующих картин для разных цветов, сдвинутых одна относительно другой в соответствии с различием в длине волны. Центральный же максимум будет общим для всех длин волн. Ближе к центру располагаются максимумы, соответствующие более коротким волнам. Длинноволновые максимумы расположены дальше, чем коротковолновые.

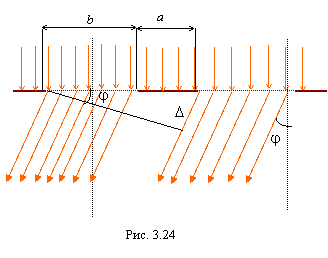Пусть свет падает на щель под углом  к нормали (рис. 3.23). Тогда разность хода между лучами от краев щели шириной b составляет , поэтому условие дифракционного минимума будет иметь вид . Центральный максимум будет наблюдаться в направлении , то есть в направлении падающей волны.

Пусть плоская волна падает на две одинаковые параллельные щели, ширина щели равна b, а ширина непрозрачного промежутка – a (рис. 3.24). Если волны, идущие в точку наблюдения от разных щелей, некогерентны, то на экране они дают одинаковые накладывающиеся друг на друга дифракционные картины, вследствие чего интенсивность в максимумах возрастет в два раза.

Если волны, идущие от разных щелей, когерентны, то дифракционная картина усложняется вследствие взаимной интерференции волн от первой и второй щелей.

В направлениях, удовлетворяющих соотношению (3.11), будут, как и при дифракции на одной щели, минимумы интенсивности, так как в этих направлениях ни одна из щелей не посылает света. Кроме того, возможны направления, в которых свет, посылаемый двумя щелями, взаимно уничтожается. Положение этих добавочных минимумов определится условием:

,

(3.12)

где , .

Если оптическая разность хода  равна целому числу длин волн, то волны, идущие от разных щелей, усиливают друг друга и дают максимумы интенсивности. Направления, соответствующие максимумам интенсивности, определятся условием:

,

(3.13)

где

Таким образом, из (3.12) и (3.13) видно, что между двумя главными максимумами располагается один добавочный минимум, а максимумы становятся более узкими, чем при дифракции на одной щели. Увеличение числа щелей делает это явление еще более отчетливым.