3.3. Зоны Френеля

Вычисления по формуле (3.2) представляют в общем случае трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.

Ч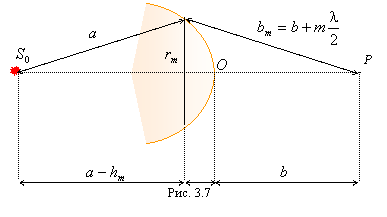 тобы понять суть метода, разработанного Френелем, определим амплитуду светового колебания, возбуждаемого в точке  сферической волной, распространяющейся в изотропной однородной среде от источника  (рис. 3.7). Фронт такой волны симметричен относительно прямой . Разобьем поверхность фронта на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки  отличаются на  (где  – длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны называются зонами Френеля.

Если расстояние от вершины поверхности О до точки Р равно b, то расстояние от внешнего края -й зоны до точки Р равно . Колебания, приходящие в точку Р от аналогичных точек двух соседних зон (то есть от точек, лежащих в середине зон или у внешних краев зон и тому подобное), находятся в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на .

Покажем, что площади всех зон Френеля примерно одинаковы. Внешняя граница -й зоны выделяет на волновой поверхности сферический сегмент высоты . Обозначим площадь этого сегмента . Тогда площадь -й зоны можно представить в виде , где  – площадь сферического сегмента, выделяемого внешней границей -й зоны. Из рис. 3.7 видно, что , где  – радиус волнового фронта,  – радиус внешней границы m-й зоны. Тогда

,

(3.3)

.

(3.4)

Для не слишком больших значений  и ввиду малости l можно пренебречь в (3.4) слагаемым, содержащим . В этом приближении

.

(3.5)

Площадь сегмента равна произведению длины окружности, ограничивающей сегмент, на высоту сегмента. Следовательно, площадь -й зоны будет равна:

.

(3.6)

Полученное выражение не зависит от m. Это означает, что при принятых допущениях площади зон Френеля примерно одинаковы.

Из равенства (3.3) легко найти радиусы этих зон. Высота сегмента , поэтому можно считать, что . Подставив значение (3.5) для , получим, что радиус внешней границы -й зоны равен:

.

(3.7)

Так как расстояние от зоны до точки Р медленно растет с увеличением номера зоны m, и угол j между нормалью к элементам зоны и направлением на точку Р также растет, то амплитуда колебания, возбуждаемого зонами Френеля в точке Р, монотонно убывает с ростом номера зоны. Даже при очень больших , когда площадь зоны начинает заметно расти с увеличением , убывание множителя  перевешивает рост , так что амплитуда продолжает убывать. В результате амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, монотонно убывают:

Фазы колебаний, возбуждаемых соседними зонами, отличаются на . Поэтому амплитуда результирующего колебания в точке Р может быть представлена в виде

(3.8)

В это выражение все амплитуды от нечетных зон входят с одним знаком, а от четных – с другим. Сгруппируем члены в (3.8) следующим образом:

,

(3.9)

при последнем члене будет знак плюс, если число зон нечетное, знак минус – при четном числе зон. Вследствие монотонного убывания амплитуды приближенно можно считать, что . Тогда выражения в скобках равны нулю. При полностью открытом фронте последний член суммы стремится к нулю, так как . Поэтому

.

(3.10)

Таким образом, при свободном распространении волны волновое возмущение в точке Р от всего фронта составляет половину возмущения, даваемого только одной первой зоной Френеля. Амплитуда результирующего колебания, получающегося вследствие взаимной интерференции волн, идущих к точке Р от различных участков сферической волны, меньше амплитуды, создаваемой действием центральной зоны. Действие всей волны на точку Р сводится к действию ее малого участка, меньше, чем центральная зона с площадью .

Оценим размеры зон Френеля. Длина световой волны очень мала, . Поэтому для расстояния , примерно равного 1 м, площадь действующей части волны меньше 1 мм². Следовательно, распространение света от источника  к точке Р происходит так, как если бы световой поток шел внутри очень узкого канала вдоль , то есть прямолинейно.

Хорошей иллюстрацией, подтверждающей рассуждения Френеля, может служить опыт с зонной пластинкой. Зонная пластинка представляет собой экран, состоящий из последовательности чередующихся прозрачных и непрозрачных колец, радиусы которых при выбранных значениях a, b и l удовлетворяют соотношению . Приготовленный таким образом экран называется амплитудной зонной пластинкой.

Если расположить такую пластинку на расстоянии  от точечного источника и на расстоянии  от точки наблюдения на линии, соединяющей эти две точки, то для длины волны  пластинка прикроет все четные зоны и оставит свободными все нечетные, начиная с центральной. Тогда амплитуда результирующего колебания в точке Р определится соотношением , то есть окажется значительно больше, чем при полностью открытом фронте. Усиление интенсивности света зонной пластинкой эквивалентно фокусирующему действию собирающей линзы.

Ещё большего эффекта можно добиться, не перекрывая зоны, а изменяя их фазу на π. В этом случае . Впервые это было осуществлено Робертом Вудом.. Он покрыл стекло тонким слоем лака и выгравировал на нем зонную пластинку так, что оптическая толщина нечетных зон отличалась от толщины четных зон на . Такие пластинки называют фазовыми зонными пластинками.

Зонные пластинки, так называемые линзы Френеля, находят применение не только в оптике, но и в акустике и радиотехнике для достаточно малых длин волн, при которых размеры линз получаются не слишком большими (сантиметровые радиоволны, ультразвуковые волны).
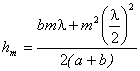