Давление зерна в силосах
Необходимость компактного размещения зернового вороха привела к созданию высоких хранилищ – сооружений в виде башен силосов.
В настоящее время используются силосы вместимостью от 100 до 1000 т. Наибольшее распространение получили силосы СКС‑3 размерами в плане 3 х 3 м и вместимостью 200 т и СКС‑6 диаметром 6 м, вместимостью 640 т.
Дальнейшее увеличение вместимости силоса за счет увеличения высоты ограничено несущей способностью грунта (обычно h ≤ 30 м).
Давление на грунт зерна массой m, находящегося в силосе диаметром D, высотой h = 30 м, будет:
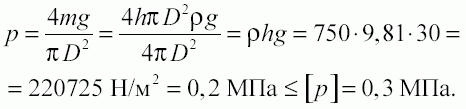
Заметим, что сила тяжести зерна в 3 раза больше силы тяжести здания (силоса).
Увеличение поперечного размера D или В вызовет потерю вместимости, рост давления на стену и момента, изгибающего стену силоса прямоугольного сечения (Ми = ρl2 / 8).
Давление зерна на стену рассчитывали приближенно как для жидкости:
(1)
или с учетом закона Кулона:
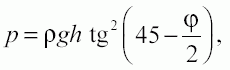
(2)
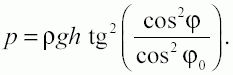
(3)
Давление зерна на дно определили как:
(4)
Очевидно, что при φ = 0 выражения (2) и (3) обращаются в выражение (1), то есть при минимально возможной сыпучести давление максимально. При φ = 90 р = 0, то есть сыпучий материал становится отвердевшим и боковое давление отсутствует.
Таким образом, с увеличением подвижности частиц относительно друг друга боковое давление на стенку силоса возрастает.
Отношение горизонтального давления к вертикальному принято называть коэффициентом бокового давления ν:
Для различных углов φ = 20–60°, φ = 15–35° ν = 0,9–0,1. Давление сыпучего материала по закону Кулона составляет 10–90 % от максимально возможного давления.
Фактически силосы, рассчитанные согласно данным выражениям, разрушались, и причиной разрушения была недооценка бокового давления (оно было большим).
Более строгое и оригинальное выражение для определения давления предложил в 1895 г. Янсен (Германия).
Рассматривая на глубине z (рис. 1.11) равновесие элементарного слоя толщиной dz, площадью А, Янсен выделил силы: давления верхнего слоя А · g; тяжести рассматриваемого слоя ρg · dz · А; трения слоя о стенки силоса pf0 · dz · L; реакции нижнего слоя A (q + dq). Здесь dq – приращение единичного вектора вертикального давления на высоте dz, z – периметр сечения, f0 – коэффициент внешнего трения сыпучего материала о стенку силоса.
Слой находится в равновесии, то есть
Откуда
Обозначив p = νq и Rг (гидравлический радиус) как Rг = A/L, получим
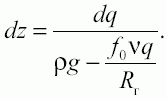
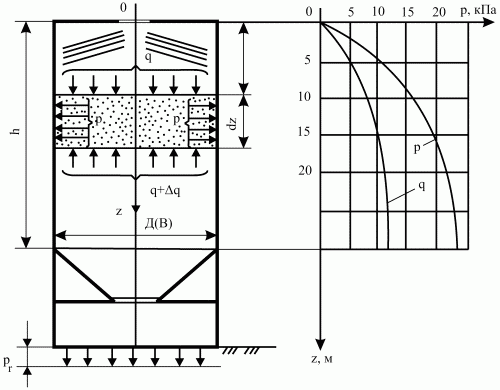
Рис. 1.11. Давление зерна в силосе.
Приняв получим и так как ρg = const, то будем иметь
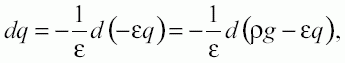
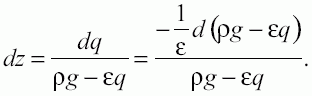
После интегрирования это выражение примет вид:
При начальных условиях z = 0, q = 0:
Откуда:
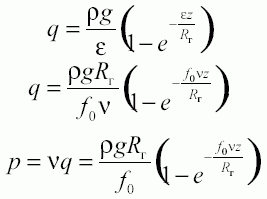
Принимая ρ = 750 кг/м3,
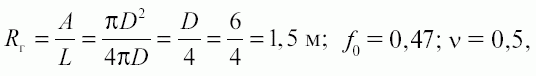
получим p = 23500(1 – е–0,157z).
Таким образом, горизонтальное давление на стену силоса зависит от внешнего трения зерна о стену, плотности продукта, диаметра и высоты силоса.
Теория Янсена дает верное представление только о характере изменения давления от высоты столба сыпучего тела. Она использовалась до 30‑х годов, но затем из‑за расхождений теоретических и экспериментальных данных, а также ряда случаев разрушения силосов стало очевидным несовершенство существующего метода расчета.
Сыпучий материал, находящийся в покое, уплотняется, возрастают коэффициент внутреннего трения (рис. 1.12) и коэффициент внешнего трения (рис. 1.13). Это приводит к тому, что величина коэффициента бокового давления изменяется от 0,3 до 0,4.
Фактически Янсен сделал ошибочное допущение, приняв ν постоянным. Но его теория впервые подтвердила так называемый «эффект силоса», то есть зависимость вертикального давления на зерно от высоты слоя только при небольших значениях h.